§51. Уравнения Максвелла для электромагнитного поля в среде с пространственно-временной дисперсией.

Запишем усреднённые уравнения Максвелла для среды:

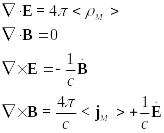(1)

, тогда первое уравнение переходит в .

В случаях, когда пространственная дисперсия существенна (кристаллооптика для СВЧ полей) не удаётся измерить оба параметра и , тогда удобно:

- это для случая кристаллооптики с учётом пространственной дисперсии.

В этом случае четвертое уравнение из системы (1) принимает вид:

Это значит, что , т.е. и для описания среды остаётся только

§52. Волновое уравнение в случае среды с пространственной дисперсией.

Запишем уравнения Максвелла для данного случая:

(2)

(3)

и уравнение связи . Если сторонних токов нет, то можно ещё привлечь закон Ома .

Из (2) и (3) получим волновые уравнения. Подействуем операторами:

на (2)

на (3)

тогда получаем:

(4)

(5)

Правая часть в выражении (4) и левая часть в выражении (5) совпадают, тогда:

(6)

(6) удобно записать в виде:

где - некоторый тензор.

Распишем в компонентах:

, тогда

где оператор - тензорный, дифференциальный оператор, он учитывает пространственную дисперсию.

Любое поле можно разложить по плоским монохроматическим волнам. Тогда решение уравнения сводится к нахождению и рассмотрению плоских монохроматических волн, этим плоским монохроматическим волнам соответствуют поля следующего типа:

Разложение в ряд Фурье:

Операторы заменяем по правилу:

Последнее правило действует в случае плоских монохроматических волн. Тогда имеем выражение:

Здесь введён тензор , который определяется следующим образом:

Решение уравнения зависит и от оператора в левой части, и от правой части. При мы имеем в решении нормальные волны (эти волны идут без источников).

§53. Дисперсионное уравнение.

Рассматриваем нормальные волны (т.е. источников нет). Здесь свойства волны, т.е. , определяется свойствами системы, которые заключены в тензоре

Это система однородных уравнений, решение этой системы существует, если

(*)

Выражение и есть дисперсионное уравнение.

Решая дисперсионное уравнение, находим допустимые значения волнового вектора и его направление.

Если в выражении задать направление , то найдём значение скорости распространения волнового вектора.

где - единичные антисимметричные тензоры.

Если , т.е. , - обратная к матрица, тогда

(**)

Выражение (**) удобно для случая расчета фурье-образа тензора Грина:

тогда

Переходим к Фурье:

тогда , считается по формуле (**)

§54. Нормальные электромагнитные волны в неограниченной среде.

Условие существования нормальных электромагнитных волн – это:

Неограниченная среда – упрощение задачи, т.к. снимаются граничные условия. Здесь на волны влияет только среда распространения волн.