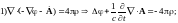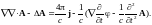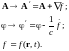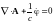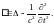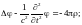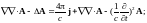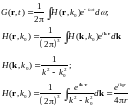- •Уравнения Максвелла. Потенциалы
- •Градиентная инвариантность
- •Калибровки
- •Функция Грина. Интеграл свертки
- •Функция Грина уравнения Пуассона
- •Функция Грина волнового уравнения
- •Запаздывающие потенциалы
- •Уравнения Максвелла для электромагнитных волн
- •Плоские волны
- •Плотность потока энергии
- •Теорема Пойнтинга
- •Теорема взаимности
- •Основные понятия макроэлектродинамики
- •Линейные и нелинейные среды
- •Граничные условия
- •Уравнения Максвелла для электромагнитного поля в среде с учетом пространственно-временной дисперсии
- •Соотношения Линдхарда
- •Нормальные волны
- •Неоднородные среды
- •Диэлектрический эллипсоид
- •Симметрия кристаллов
- •Электромагнитные волны в немагнитных анизотропных средах
- •Влияние стационарного электрического поля на оптические свойства кристаллов
- •Применение эффекта Поккельса
- •Литература
Оглавление
1. Уравнения Максвелла. Потенциалы 2
2. Градиентная инвариантность 3
3. Калибровки 3
4. Функция Грина. Интеграл свертки 4
5. Функция Грина уравнения Пуассона 5
6. Функция Грина волнового уравнения 5
7. Запаздывающие потенциалы 8
8. Уравнения Максвелла для электромагнитных волн 9
9. Плоские волны 10
10. Плотность потока энергии 12
11. Теорема Пойнтинга 12
12. Теорема взаимности 13
13. Основные понятия макроэлектродинамики 14
14. Линейные и нелинейные среды 16
15. Граничные условия 17
16. Уравнения Максвелла для электромагнитного поля в среде с учетом пространственно-временной дисперсии 30
17. Соотношения Линдхарда 28
18. Нормальные волны 29
19. Неоднородные среды 30
20. Диэлектрический эллипсоид 31
21. Симметрия кристаллов 37
22. Электромагнитные волны в немагнитных анизотропных средах 39
23. Влияние стационарного электрического поля на оптические свойства кристаллов 46
24. Применение эффекта Поккельса 48
Литература 52
Уравнения Максвелла. Потенциалы
Уравнения Максвелла для электромагнитного поля в вакууме:
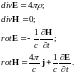
или
|
(1) |
Теорема Гаусса в операторной форме:
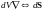
Теорема Стокса в операторной форме (рис.1):
где
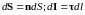
Потенциалы электромагнитного
поля:
|
( |
где
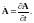
Подставим соотношения (2) в уравнения Максвелла (1):
|
(3)
|
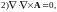 это уравнение
превращается в тождество, так как
это уравнение
превращается в тождество, так как
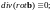
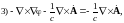 так как
так как
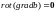 получим тождество
получим тождество
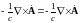
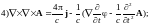
Раскрыв двойное векторное произведение, получим:
|
(4)
|
Градиентная инвариантность
Если
заданы потенциалы А
и
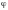 ,
то этим вполне однозначно задаются
Е
и Н,
а
значит, и поле. Однако одному полю могут
соответствовать разные потенциалы
[2,
§ 18]:
,
то этим вполне однозначно задаются
Е
и Н,
а
значит, и поле. Однако одному полю могут
соответствовать разные потенциалы
[2,
§ 18]:
|
(5) |
При таком переходе
 и
и
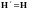
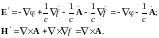
Таким образом, физический смысл имеют лишь те величины, которые инвариантны по отношению к преобразованию потенциалов (5). Поэтому все уравнения должны быть инвариантны относительно этого преобразования. Эту инвариантность называют градиентной (калибровочной).
Калибровки
Калибровками называются дополнительные ограничения, которые накладываются на потенциалы А и , чтобы уравнения для потенциалов в конкретном случае были удобны для решения.
1. Калибровка Лоренца:
|
(6) |
С учетом градиентной инвариантности (5) из (6) получим:
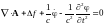
Отсюда
следует условие, ограничивающее вид
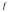 в градиентном преобразовании:
в градиентном преобразовании:
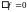 ,
где □ - оператор Даламбера,
,
где □ - оператор Даламбера,
|
(7) |
Из
уравнения Максвелла
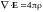 в
формуле (3) с учетом уравнения (6)
получим:
в
формуле (3) с учетом уравнения (6)
получим:
|
(8) |

Для
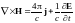 получим:
получим:
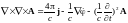
Подставим
в (5)
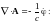
|
(9) |

2. Калибровка Кулона:
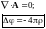
Условие на f:
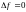
3. Калибровка поперечных волн:
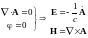
Функция Грина. Интеграл свертки
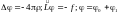
Функция Грина позволяет найти частное решение неоднородного дифференциального уравнения.
Пусть
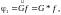 где
* означает интеграл свертки; G
-
ядро оператора Грина.
где
* означает интеграл свертки; G
-
ядро оператора Грина.
Тогда
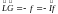 .
Отсюда
следует, что оператор Грина должен
удовлетворять уравнению
.
Отсюда
следует, что оператор Грина должен
удовлетворять уравнению
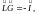
или через функцию Грина
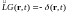 .
.
Решение через функцию Грина имеет вид:
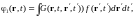
 здесь
интеграл берется по объему, где источник
поля не равен нулю.
здесь
интеграл берется по объему, где источник
поля не равен нулю.
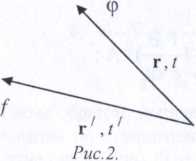
Функция Грина устанавливает связь между источником и наблюдателем (рис.2).
Плотность заряда точечного
источника
имеет вид:
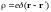
В этом легко убедиться:
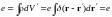 .
.
Функция Грина уравнения Пуассона
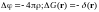
Функция
Грина уравнения Пуассона представляет
потенциал точечного источника при
условии, что заряд равен
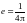 и
расположен в начале координат:
и
расположен в начале координат:
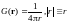
Решение для произвольного распределения плотности заряда имеет
вид:
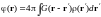
Подействовав с левой стороны оператором Лапласа и применив определения функции Грина и дельта-функции, получим:
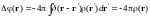
Функция Грина волнового уравнения
Для нахождения функции Грина воспользуемся преобразованиями Фурье:
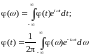
В частности, для фурье-образа дельта-функции получим:
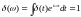
Использование фурье-преобразований позволяет перейти от дифференциальных уравнений к алгебраическим по правилам замены операторов алгебраическими множителями:
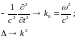
Функция
Грина оператора Даламбера:
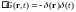
Перейдем к фурье-образу по времени:
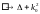 -
оператор Гельмгольца;
-
оператор Гельмгольца;
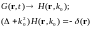
Перейдем к фурье-образу по координатам:
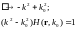
Связь фурье-образа с прообразом:
|
(10)
|
Вычислим интеграл (10). Перейдем к сферическим координатам:
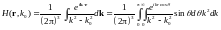
Проинтегрируем по углу:
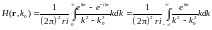
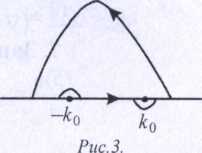 Данный
интеграл находится с помощью теоремы
о вычетах [5, с. 212]. Знаменатель имеет
два полюса: k=+k0.
Оба они лежат на действительной оси.
Выберем контур интегрирования, как
показано на рис.З. Вычет подынтегральной
функции в точке k0
(полюс первого порядка) равен
Данный
интеграл находится с помощью теоремы
о вычетах [5, с. 212]. Знаменатель имеет
два полюса: k=+k0.
Оба они лежат на действительной оси.
Выберем контур интегрирования, как
показано на рис.З. Вычет подынтегральной
функции в точке k0
(полюс первого порядка) равен
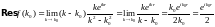
Тогда
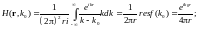
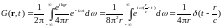
Здесь воспользовались свойством четности дельта-функции. Перейдя к исходным переменным
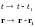
получим:
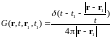
Сделаем замену переменных:
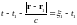
где
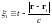
Это
дает:
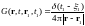

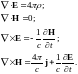
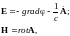
 2)
2)