Занятие 1.1.5. Спектральный анализ непериодических сигналов

Вопросы:

1. Преобразования Фурье

2. Соотношения между спектрами одиночных и периодических сигналов

3. Основные свойства спектральной плотности

Преобразования Фурье

В ряд Фурье раскладывается только периодический сигнал. Возникает вопрос как отыскать спектральный состав непериодического сигнала, например одиночного импульса.

Сначала предположим, что это был периодический сигнал с периодом T, т.е. добавим слева и справа бесконечное количество таких же импульсов. Получили периодический сигнал . Этот сигнал можно представить в виде ряда Фурье

- частота повторения

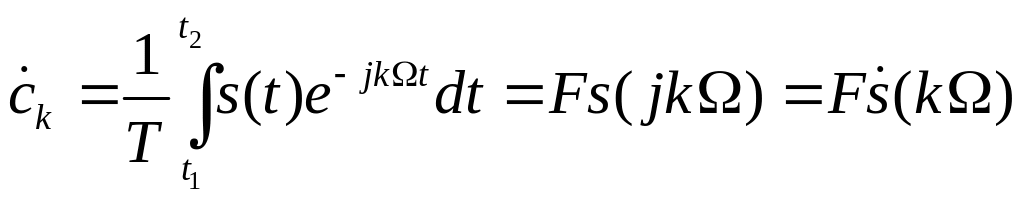
Теперь устремляем период в бесконечность, таким образом периодический сигнал превращаем в одиночный.

- дискретные частоты заменяются непрерывными

Расстояние между отдельными гармониками спектра становятся бесконечно малыми, а спектр – сплошным. В спектре непериодического сигнала присутствуют колебания всех частот от 0 до .

- обратное преобразование Фурье.

Величина или - спектральная плотность сигнала.

Спектральная плотность обладает свойствами коэффициентов комплексного ряда Фурье. Отличается только сомножителем .

Спектральная плотность показывает распределение комплексных амплитуд гармоник в спектре сигнала по частотам.

Спектральная плотность есть некоторая математическая абстракция, поскольку она определена и для отрицательных, и для положительных частот. Т.е. если мы изобразим модуль спектральной плотности, он будет и слева, и справа.

Спектральная плотность может быть применена как к периодическому, так и к непериодическому сигналу. Форма спектральной плотности зависит только от формы сигнала и не зависит от периода. Т.е. у одиночного импульса и периодического импульса (такого же по форме), спектральная плотность будет одинакова. Из определения спектральной плотности видно, что её можно представить в следующей форме .

- модуль спектральной плотности

- аргумент спектральной плотности

Прямое преобразование Фурье позволяет получить спектральную плотность сигнала зная сам сигнал. Спектральная плотность – это математическая абстракция, но она помогает найти реальный спектр сигнала. Обратное преобразование Фурье помогает найти сигнал, зная его спектральную плотность.

Соотношение между спектрами одиночных и периодических сигналов

Сравним выражение для коэффициентов ряда Фурье и прямое преобразование Фурье. Они похожи, различие в том, что дискретные частоты в коэффициентах Фурье заменены непрерывной частотой в преобразовании Фурье и коэффициент отсутствует в преобразовании Фурье. Тогда коэффициенты ряда Фурье можно выразить через спектральную плотность.

при условии замены непрерывной частоты на дискретные.

. Тогда комплексная амплитуда k-ой гармоники в спектре периодического сигнала

- аргумент спектральной плотности, взятый на соответствующих частотах.

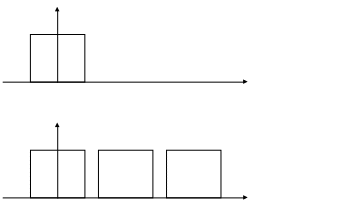
Спектр второго сигнала можно найти с помощью ряда Фурье. Спектр непериодического сигнал находится следующим образом:

с помощь второго преобразования Фурье находится спектральная плотность. Её модуль для прямоугольного импульса будет такой:

РИСУНКИ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ

Чтобы найти амплитудно-частотный спектр непериодического сигнала необходимо:

1. Выкинуть левую половину из спектральной плоскости.

2. Умножить модуль спектральной плотности на 2 и заштриховать всё под этой линией.

Чтобы получит фазочастотный спектр непериодического сигнала, надо убрать левую часть в аргументе спектральной плотности.

Спектр периодического сигнала тоже можно получить, пользуясь понятием спектральной плотности.

1. Прямым преобразованием Фурье ищем спектральную плотность. Для периодического сигнала такой же формы, как и одиночного импульса, она будет одинаковой.

Например для прямоугольного импульса модуль спектральной плоскости будет таким:

РИСУНОК

2. Стираем левую часть.

3. Умножаем правую часть на , где 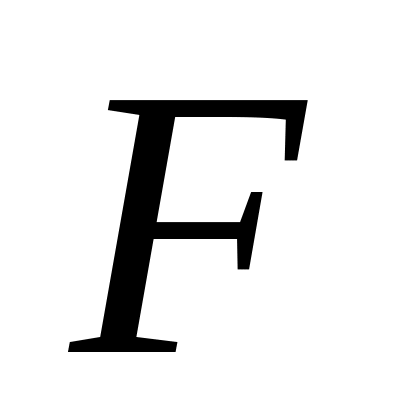- частота повторения и расставляем под этой кривой палочки, следующие на расстоянии .

Для получения фазочастотного спектра берём аргумент данной плотности, убираем отрицательные частоты расставляем палочки на том же расстоянии .

Таким образом спектр периодического сигнала можно получить с помощью ряда Фурье, а можно с помощью спектральной плотности. Спектр же непериодического сигнала можно получить только с помощью спектральной плотности, поскольку в ряд он не рассказывается.

Основные свойства спектральной плотности

Часто в радиотехнике возникает следующая задача: зная спектр одного сигнала, не делая преобразований Фурье, найти спектр другого сигнала, при этом сигналы должны быть связаны друг с другом.

РИСУНОК

Свойства спектральной плотности:

1. Модуль спектральной плотности – всегда чётная функция

2. Аргумент спектральной плотности – функция нечётная

3. Сдвиг сигнала во времени. РИСУНОК!!! . Если сигналу , то , т.е. модуль спектральной плотности не изменится, а начальные фазы получат добавку , пропорциональную частоте.

4. Изменение масштаба во времени. РИСУНОК!!! . Отсюда получаем , что если , то . Это фундаментальное положение спектрального анализа сигнала: во сколько раз уменьшится длительность импульса, во столько же раз расширится его спектр, но при этом уменьшатся амплитуды составляющих спектра.

5. Сложение сигналов. Если 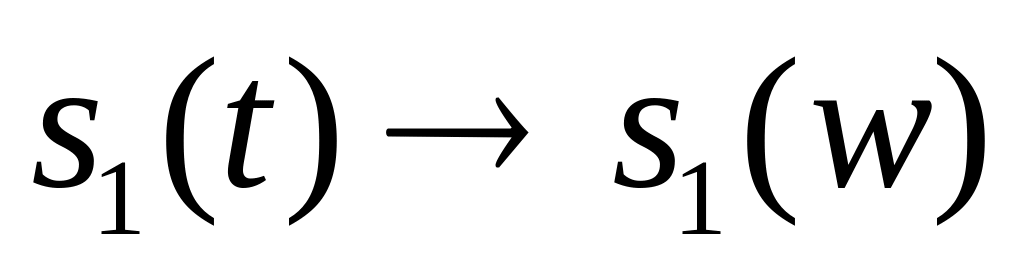, 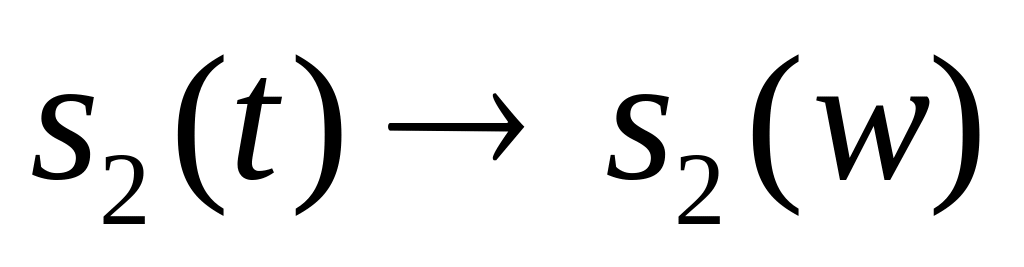то 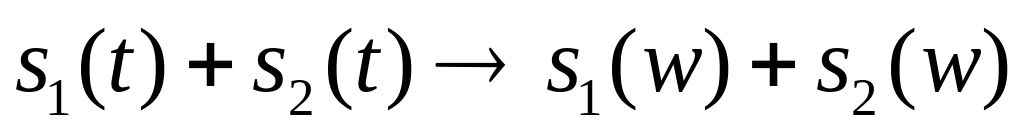. Это правило распространяется на какое угодно количество сигналов.

6. Дифференцирование и интегрирование сигналов. Пусть сигналу соответствует спектральная плотность . Тогда . за исключением .

7. Спектральная плотность при нулевой частоте. 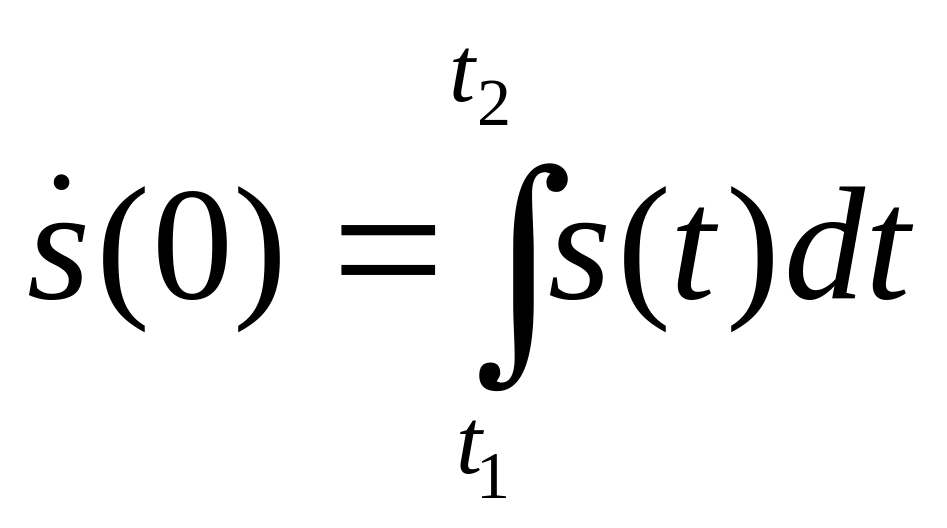- интеграл от сигнала. Т.е. постоянная составляющая – есть площадь сигнала. Однако если сигнал симметричен оси времени, значит постоянной составляющей в нём нет. У любого сигнала. Не симметричного относительно оси времени будет постоянная составляющая.