- •Радиотехнические цепи и сигналы
- •Введение
- •Тема 1.1. «Общие сведения о сигналах и их спектральный анализ»
- •Занятие 1.1.3. Спектральный анализ детерминированных сигналов
- •Занятие 1.1.5. Спектральный анализ непериодических сигналов
- •Преобразования Фурье
- •Соотношение между спектрами одиночных и периодических сигналов
- •Энергетический спектр сигнала
- •Занятие 1.1.7. Спектральные плотности типовых элементарных сигналов
- •Дельта импульс
- •Гауссов импульс
- •Тема 1.2. Радиосигналы и их спектральный анализ Занятие 1.2.1. Амплитудно-модулированные сигналы
- •3 Картинки
- •2 Картинки
- •2 Картинки
- •Радиосигналы с угловой модуляцией
- •2 Картинки
- •Тема 1.3. Дискретные и цифровые сигналы
- •1.3.1. Общие сведения о дискретных и цифровых сигналах
- •Дискретизация и квантование. Классификация дискретных сигналов
- •3 Картинки
- •3 Картинки с односторонней и двусторонней шим
- •3 Каритнки с фазоимпульсной и частотно-импульсной модуляцией
- •1.3.2 Спектральный анализ дискретных сигналов
- •1.3.3. Цифровые сигналы
- •Радиотехнические цепи
- •Характеристики и уравнения пассивных и активных элементов цепи
- •2.1.2 Переменный (гармонический) ток и его основные характеристики
- •2 Картинки
- •3 Картинки
- •Действующее и среднее значение гармонических величин
- •2 Картинки
- •Метод комплексных амплитуд
- •Тема 2.2. Четырёхполюсники Занятие 2.2.1. Уравнения и системы параметров четырёхполюсников
- •Вторичные параметры и схемы соединений четырехполюсников
- •Частотно-избирательное свойство линейных цепей. Электрические фильтры Занятие 2.3.1. Общие сведения частотно-избирательных цепях
- •Электрические фильтры
- •Частотные характеристики основных типов фильтров
- •Тема 2.6. Связанные колебательные контуры Занятие 2.6.1. Связанные колебательные контуры
- •Передача и преобразование сигналов линейными цепями Метод дифференциальных уравнений
- •4 Рисунка
- •3. 5. Цифровые фильтры
Занятие 1.1.3. Спектральный анализ детерминированных сигналов
Вопросы:
Ряды Фурье.
Спектр периодического сигнала (АЧС, ФЧС).
Ряды Фурье
В большинстве
случаев сигналы являются сложной
функцией времени. Это усложняет задачу
анализа прохождения сигналов через
радиотехнические цепи. Для решения
данной задачи сложный сигнал нужно
представить в виде суммы более простых.
Из математики известно, что любая функция
f(x),
удовлетворяющая условиям Дирихле
(ограниченность функции), можно представить
в виде ряда
![]() .
В этой формуле
.
В этой формуле
![]() -
элементарные функции,
-
элементарные функции,
![]() -
коэффициенты. Такое представление
называется разложением по базисным
функциям. Выбор наиболее рациональной
системы базисных функций зависит от
поставленной задачи. Например, для
теоретического анализа сигнала
целесообразно выбирать систему функций,
обеспечивающую наиболее быстрое
схождение данного ряда. Например,
полиномы Чебышева, Эрнитта, Лежандра.
Когда требуется наиболее точное
представление сигнала минимальным
количеством слагаемых, используются
тригонометрические функции простых
аргументов (синусов и косинусов). Это
удобно по следующим причинам: гармоника
– это единственный сигнал, который не
меняет свою форму при прохождении через
линейную цепь; можно использовать
символьный метод анализа прохождения
сигналов через цепь. Поэтому разложение
по тригонометрическому базису очень
широко применяется в радиотехнике.
-
коэффициенты. Такое представление
называется разложением по базисным
функциям. Выбор наиболее рациональной
системы базисных функций зависит от
поставленной задачи. Например, для
теоретического анализа сигнала
целесообразно выбирать систему функций,
обеспечивающую наиболее быстрое
схождение данного ряда. Например,
полиномы Чебышева, Эрнитта, Лежандра.
Когда требуется наиболее точное
представление сигнала минимальным
количеством слагаемых, используются
тригонометрические функции простых
аргументов (синусов и косинусов). Это
удобно по следующим причинам: гармоника
– это единственный сигнал, который не
меняет свою форму при прохождении через
линейную цепь; можно использовать
символьный метод анализа прохождения
сигналов через цепь. Поэтому разложение
по тригонометрическому базису очень
широко применяется в радиотехнике.
Спектром сигнала называется совокупность простейших колебаний, дающих при суммировании данный сигнал. Очень широко в радиотехнике используется частотный спектр, представляющий совокупность гармонических колебаний, каждое из которых характеризуется своей частотой, амплитудой и начальной фазой. В этом случае говорят, что сигнал представлен в виде ряда Фурье. Наиболее применима теории цепей и сигналов комплексная форма ряда Фурье для периодического сигнала.

В этой формуле:
k = 0, 1, 2…
![]() -
частота повторения периодического
сигнала.
-
частота повторения периодического
сигнала.
Коэффициент
![]() называется коэффициент ряда Фурье и
определяется как
называется коэффициент ряда Фурье и
определяется как
![]() ,
который является комплексной амплитудой
k-ой
гармоники.
,
который является комплексной амплитудой
k-ой
гармоники.
Таким образом, в спектре любого периодического сигнала содержится бесконечное количество гармоник с частотами, кратными частоте повторения сигнала.
Коэффициент
-
это комплексное число, которое можно
представить в виде
![]() .
.
определяет амплитуду k-й гармоники в спектре
![]() - определяет фазу
k-й
гармоники в спектре
- определяет фазу
k-й
гармоники в спектре

От показательной
комплексной формы нетрудно перейти к
вещественной форме ряда Фурье. Для этого
выделим в ряду Фурье парные слагаемые,
например
![]() и
и
![]() и учтём, что
и учтём, что
![]() а
а
![]() .
Тогда
.
Тогда
![]() .
.
Применим формулу
Эйлера для косинуса
![]() .
.
![]()
Аналогично
![]() и
и
![]() получим
получим
![]() .
.
Все коэффициенты
парные, за исключением 0-го. Таким образом,
в вещественной форме сигнал s(t)
представляется в виде
![]() .
Графически спектр сигнала удобно
изображать в виде амплитудно-частотного
спектра АЧС и фазочастотного спектра
ФЧС.
.
Графически спектр сигнала удобно
изображать в виде амплитудно-частотного
спектра АЧС и фазочастотного спектра
ФЧС.
АЧС – это зависимость амплитуд k-ых гармоник от частоты.
ФЧС – это зависимость начальных фаз k-ых гармоник от частоты.
ГРАФИКИ СПЕКТРОВ АЧС И ФЧС
Пример: найти частотный спектр периодической последовательности прямоугольных видеоимпульсов.

Очевидно, что
интегрировать можно от
![]() до
до
![]()
 .
.
Воспользуемся формулой Эйлера для синуса:
![]()
Тогда
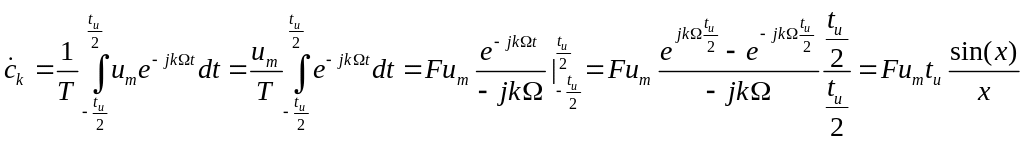
![]()
![]()