§14 Функция распределения и плотность вероятности непрерывной случайной величины, их взаимосвязь и свойства

Определение и свойства функции распределения сохраняются и для непрерывной случайной величины, для которой функцию распределения можно считать одним из видов задания закона распределения. Но для непрерывной случайной величины вероятность каждого отдельного ее значения равна 0. Это следует из свойства 4 функции распределения:

р(Х = а) = F(a) –  F(a) = 0.

Поэтому для такой случайной величины имеет смысл говорить только о вероятности ее попадания в некоторый интервал.

Вторым способом задания закона распределения непрерывной случайной величины является так называемая плотность вероятности (плотность распределения, дифференциальная функция).

Определение. Функция f(x), называемая плотностью вероятности непрерывной случайной величины, определяется по формуле: f (x) = F′(x), то есть является первой производной от функции распределения.

Для описания дискретной случайной величины плотность вероятности неприемлема.

Смысл плотности вероятности состоит в том, что она показывает, как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.

После введения функций распределения и плотности вероятности можно дать следующее определение непрерывной случайной величины.

Определение. Случайная величина Х называется непрерывной, если ее функция распределения F(x) непрерывна на всей оси ОХ, а плотность вероятности f(x) существует везде, (за исключением может быть, конечного числа точек).

Зная плотность вероятности, можно вычислить вероятность того, что некоторая случайная величина Х примет значение, принадлежащее заданному интервалу.

Теорема (основное свойство плотности вероятности). Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности вероятности, взятому в пределах от a до b: .

Доказательство этой теоремы основано на определении плотности вероятности и 4-ом свойстве функции распределения, записанном выше.

Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми x=a и x=b.

Функция распределения может быть легко найдена, если известна плотность вероятности, по формуле:

Свойства плотности вероятности

Свойство 1. Плотность вероятности – неотрицательная функция f(x) ≥ 0, так как функция распределения является неубывающей.

Свойство 2. Несобственный интеграл от плотности вероятности в пределах от -  до  равен единице: .

Его справедливость следует из того, что а

Свойство 3. так как при

Пример 1. Плотность вероятности непрерывной случайной величины задана формулой

Найти: а) значение константы С; б) вид функции распределения; в) .

Решение.

а) значение константы С найдем из свойства 2:

откуда .

б) вид функции распределения найдем по формуле :

в) вероятность

Пример 2. Функция распределения непрерывной случайной величины имеет вид: . Найти плотность вероятности.

Решение. По определению плотности f (x) = F′(x): .
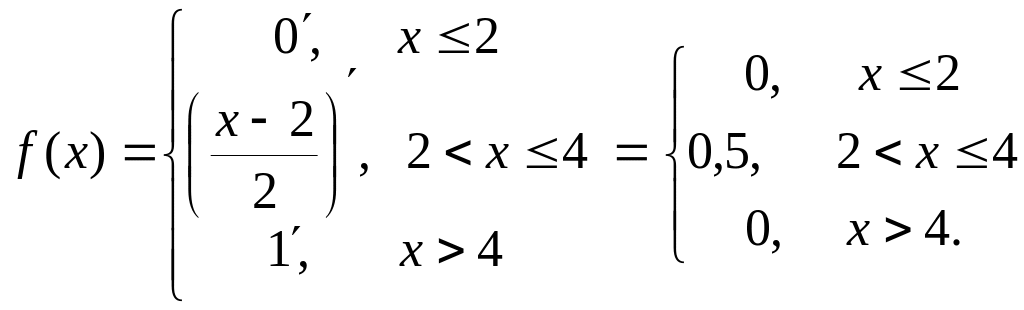