МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ИВАНОВСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

Кафедра высшей и прикладной математики

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к практической работе

по оцениванию параметров и проверке гипотез

о нормальном распределении

Иваново 2012

Составитель Ю. С. Ахмадулина

УДК 005.336.3:004(075.8)

Методические указания к практической работе по оцениванию параметров и проверке гипотез о нормальном распределении / Иванов. гос. архит. -строит. унив.; cост. Ю. С. Ахмадулина. Иваново, 2012. – 21 с.

В методических указаниях рассматриваются статистические методы, используемые в задачах по оцениванию параметров и проверке гипотез о нормальном распределении.

Методические указания ставят своей целью формирование у обучающихся знаний, умений и приобретение опыта применения статистических методов (теории вероятностей, элементов математической статистики, статистических методов контроля и управления качеством) при анализе и синтезе технологических процессов производства.

Библиогр.: 5 назв.

Содержание

Стр.
1. Построение интервального вариационного ряда распределения…..	4
2. Вычисление выборочных характеристик распределения………..	5
3. Графическое изображение вариационных рядов…………………	7
4. Расчет теоретической нормальной кривой распределения………	10
5. Проверка гипотезы о нормальном законе распределения по критерию Пирсона…………………………………………………….	11
6. Проверка гипотезы о нормальном законе распределения по критерию Романовского……………………………………………..	13
7. Задание для самостоятельной работы по оцениванию параметров и проверке гипотезы о нормальном законе распределения………..	13
Приложение…………………………………………………………….	18
Библиографический список……………………………………………	21

Оценивание параметров и проверка гипотезы о нормальном законе распределения

Методику оценивания параметров и проверки гипотезы о нормальном распределении выборочных данных рассмотрим на примере.

Пример. По результатам выборочного обследования 100 однотипных изделий получены данные о линейном размере диаметров втулок (табл. 1).

Таблица 1

Линейный размер диаметров 100 втулок (мм)

5,56 5,33 5,54 5,43 5,43 5,64 5,40 5,71 5,79 5,39

5,27 5,47 5,43 5,43 5,43 5,43 5,68 5,47 5,58 5,85

5,03 5,33 5,64 5,47 5,61 5,33 5,43 5,21 5,27 5,47

5,47 5,33 5,21 5,27 5,47 5,11 5,54 5,33 5,33 5,27

5,27 5,47 5,68 5,68 5,27 5,33 5,43 5,43 5,40 5,58

5,37 5,05 5,43 5,43 5,54 5,33 5,37 5,33 5,43 5,43

5,47 5,33 5,79 5,47 5,61 5,33 5,37 5,43 5,54 5,43

5,47 5,47 5,47 5,79 5,54 5,54 5,21 5,27 5,54 5,33

5,33 5,68 5,21 5,47 5,64 5,64 5,64 5,21 5,54 5,61

5,11 5,11 5,47 5,54 5,54 5,64 5,64 5,54 5,81 5,54

1. Построение интервального вариационного ряда распределения.

1. Определите среди имеющихся наблюдений (табл. 1) минимальный x_min и максимальный x_max значения признака. В данном примере это будут x_min=5,03 и x_max=5,85.

2. Определите размах варьирования признака

.

3. Определите длину частичного интервала по формуле Стерджеса:

, где n – объём выборки.

(мм).

4. Определите граничные значения интервалов 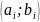. Так как и 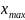являются случайными величинами, рекомендуется отступить влево от нижнего предела варьирования . За нижнюю границу первого интервала примите величину, равную . Если окажется, что , хотя по смыслу величина положительная, то можно принять .

Верхняя граница первого интервала .

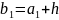В рассматриваемом примере граничные значения составят:

; ; ;

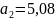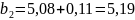и т.д.

Границы последовательных интервалов записывают в графе 1 табл. 2.

Таблица 2

Интервальный ряд распределения линейных размеров

диаметра 100 втулок

1	2	3
Интервалы	Частота	Накопленная частота
4,97 – 5,08	2	2
5,08 – 5,19	3	5
5,19 – 5,30	12	17
5,30 – 5,41	19	36
5,41 – 5,52	29	65
5,52 – 5,63	18	83
5,63 – 5,74	13	96
5,74 – 5,85	4	100

5. Группировка результатов наблюдений.

Просматриваем статистические данные в том порядке, в каком они записаны в табл. 1, и значения признака разносим по соответствующим интервалам. В каждый интервал значения признака включаются варианты, строго большие левой границы, и меньшие либо равные правой границы. В результате получим интервальный статистический ряд распределения частот (табл. 2, графы 1, 2).

Примечание. Число интервалов обычно выбирают равным от 7 до 11 в зависимости от числа наблюдений и точности измерений с таким расчетом, чтобы интервалы были достаточно наполнены частотами. Если получают интервалы с нулевыми частотами, то нужно увеличить ширину интервала (особенно в середине интервального ряда).