1.3. Карта ввода криволинейных координат
При
вводе криволинейных координат для
описания движения материальной точки
могут возникнуть ситуации, когда
предлагаемые в качестве таких координат
переменные
удовлетворяют условиям определения 1
не для всех точек абсолютного пространства,
а лишь только для некоторого множества
.
В таких ситуациях ввод обобщенных координат осуществляется путем представления пространства объединением подмножеств и подбора криволинейных координат для каждого подмножества в отдельности.
Общая схема алгоритма ввода обобщенных координат такова.
Если по предварительным прогнозам из каких-либо соображений известно, что на изучаемых моделях движения материальная точка не покинет указанное выше множество точек абсолютного пространства, то переменные могут быть приняты за обобщенные координаты.
Если нет такой уверенности, то можно поступить следующим образом.
Ввести криволинейные координаты для множества части пространства, в которой выполняются условия, указанные в определении 1.
Для оставшейся части пространства следует подобрать другие переменные
так, чтобы в этой части для них выполнялось
определение 1. Причем, новые переменные
вводятся так, чтобы не нарушались
условия из определения криволинейных
координат и в некотором подмножестве
множества
.
При таком выборе и переменные
,
и переменные
будут обобщенными координатами точек
подмножества
.
Общая
часть пространства для переменных
и
позволяет при изучении движений
осуществлять переход от криволинейных
координат
к криволинейным координатам
,
как только материальная точка окажется
в этой общей части пространства.
Если после ввода переменных
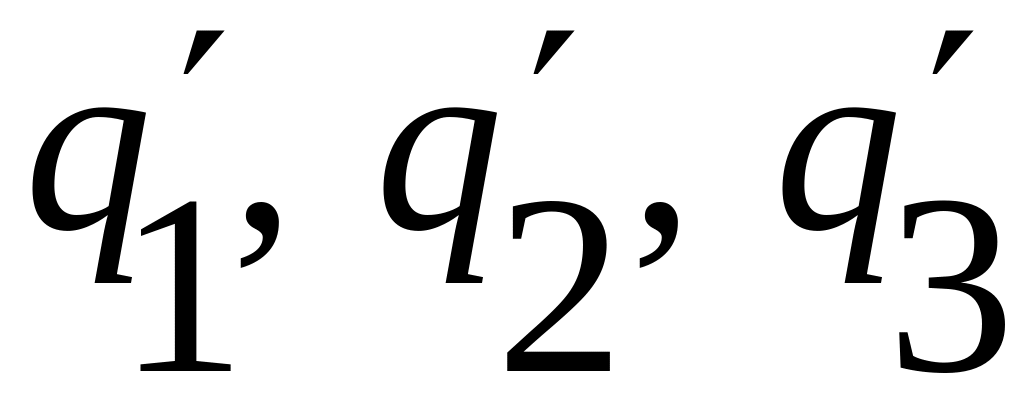осталась все еще непокрытой какая–либо
часть пространства допустимых положений
точки, то подобным образом вводится
следующая группа обобщенных координат,
покрывающая эту часть или какое-либо
множество положений в ней.
Так следует поступать до тех пор, пока не будет покрыто все абсолютное пространство.
Процесс конечен, поскольку на любом этапе можно его завершить, приняв в оставшемся непокрытым множестве в качестве криволинейных координат декартовые координаты точки.
Итогом такого построения будет являться карта ввода криволинейных координат точки, охватывающая все пространство возможных положений точки.