§2. Естественный способ задания движения точки
5º. Кинематический способ вычисления кривизны кривой
5.1. Кинематическая формула радиуса кривизны
Из формулы Гюйгенса (1.2.16)
(1.2.16)
находим
.
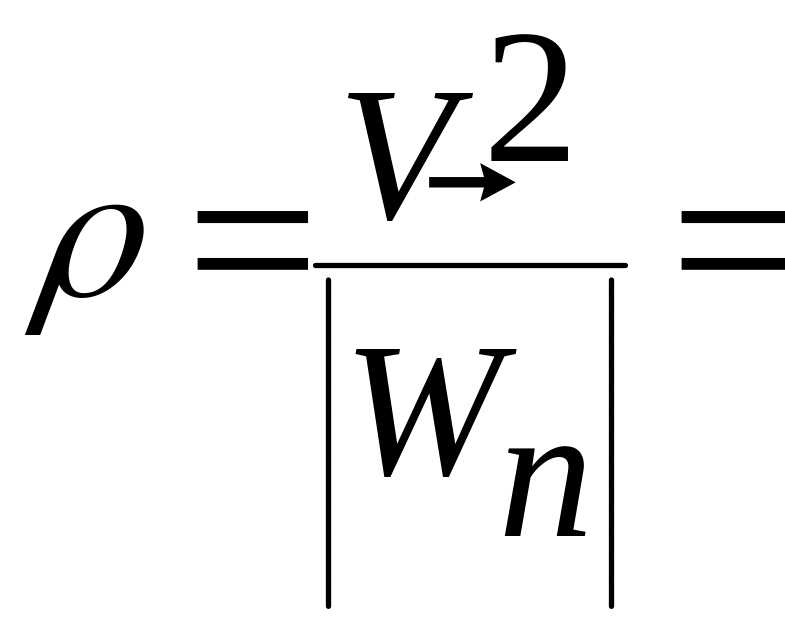
(1.2.17)
Покажем, что
.
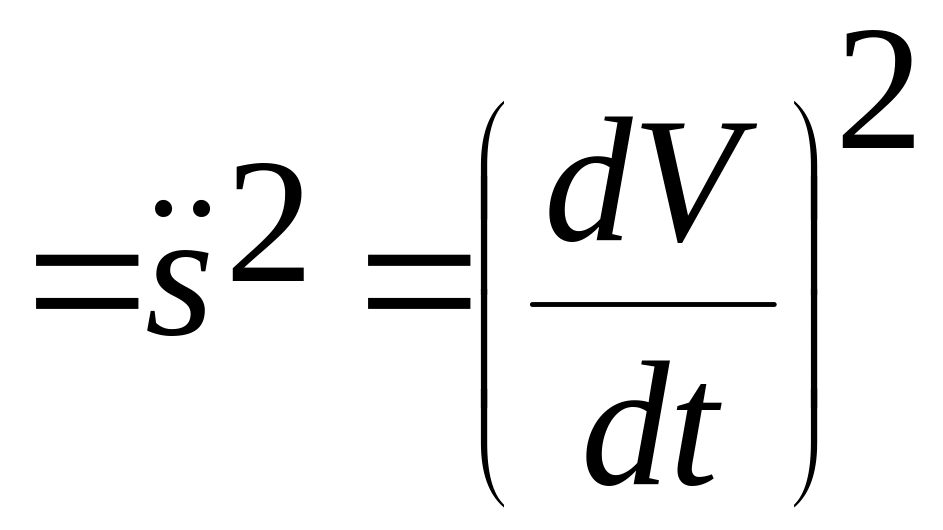(1.2.18)
Действительно, из (1.2.15):
,
(1.2.15)
следует соотношение
.
Дифференцируя
это
равенство
по
,
получим
.
Возводим в квадрат и, учитывая, что
,
приходим к соотношению
.
Отсюда следует равенство (1.2.18):
.
Таким образом, формула (1.2.17):
, (1.2.17)
где
, (1.2.18)
позволяет
вычислить радиус кривизны, если
известны
,
и
.
5.2. Алгоритм построения радиуса кривизны кривой
Алгоритм
расчета величины радиуса кривизны
в регулярной точке кривой строится на
основе кинематических формул (1.2.17) и
(1.2.18).
Пусть гладкая кривая задается параметрическим способом:
,
,
,
.
(1.2.19)
1).
Задаем какое-либо движение
по кривой.
Например,
в качестве
берем функцию 
.
2).
Вычислим величины
и
.
На заданном движении, будем иметь:
,
,
.
Здесь
— заданные функции (1.2.19).
По
величинам
,
,
находим
:
Аналогично, для вычисления ускорения дифференцированием координат скорости находим выражения для координат ускорения:
,
,
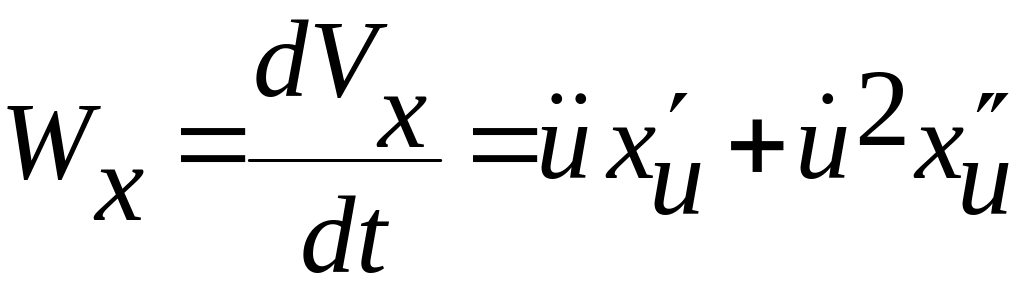(1.2.20)
.
Подставляя правые части (1.2.20) в формулу для квадрата модуля ускорения:
,
вычисляем .
3).
Определяем величину
.
Формулу для расчета получаем через последовательность следующих очевидных соотношений:
.
4). Значение радиуса кривизны получим подстановкой вычисленных значений величин , , в формулу (1.2.17):
.
(1.2.17)
5.3. Пример применения алгоритма
Применение алгоритма рассмотрим на примере вычисления радиуса кривизны эллипса в любой его точке.
1. Уравнение эллипса в декартовых координатах имеет вид:
.
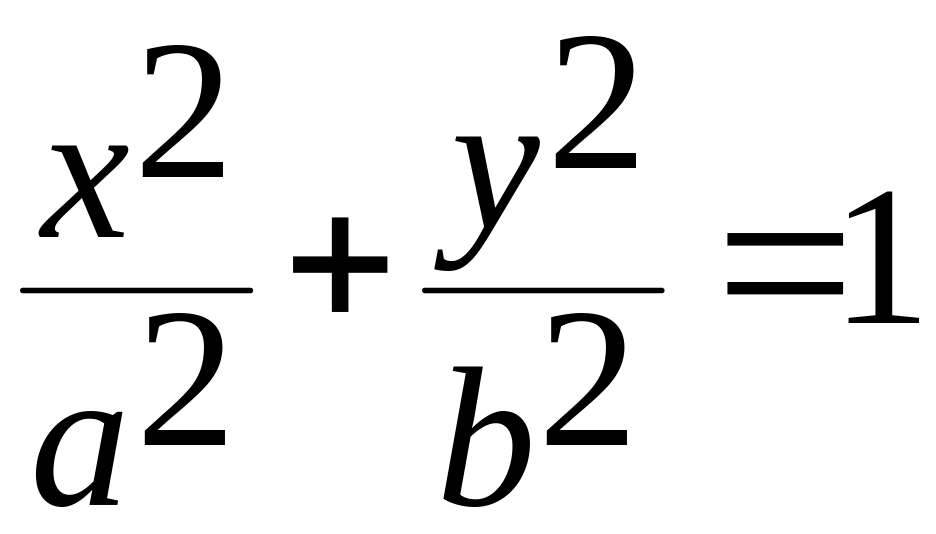2. Переходим к параметрическому уравнению эллипса:
,
.
3. Задаем закон движения по эллипсу:
.
4. Строим расчетные формулы для вычисления кинематических характеристик движения.
4.1). Формулы для скорости:
,
,
(1.2.21)
.
4.2). Формулы для ускорения:
,
,
(1.2.22)
.
4.3).
Формула для производной
:
.
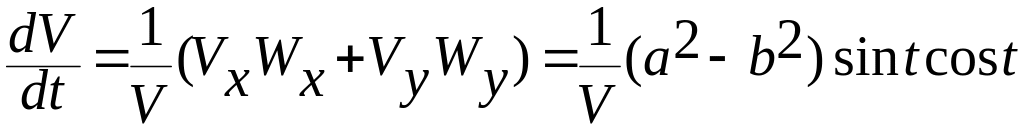(1.2.23)
4.4). Формула для расчета радиуса кривизны в любой точке эллипса:
.
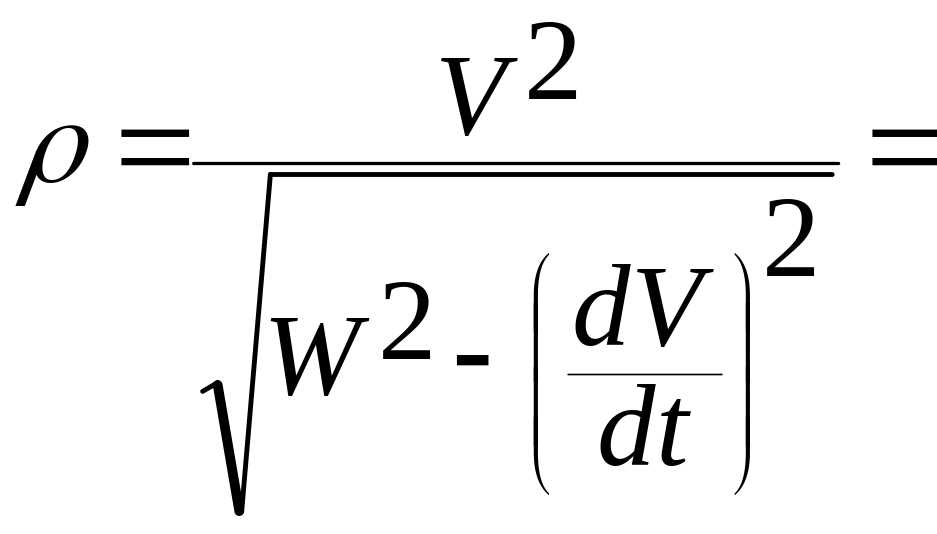
Эта формула получена подстановкой в (1.2.17)
(1.2.17)
величин , и , вычисленных по формулам (1.2.21), (1.2.22) и (1.2.23).
В декартовых координатах она будет иметь вид
.
(1.2.24)
В
частности,
если
,
то эллипс вырождается в окружность.
Тогда
,
и из (1.2.24) получим
в любой точке окружности.
Пусть
.
Вычисляем
в вершинах эллипса.
В
вершинах на оси 
имеем
.
Для них из (1.2.24)
получим
.
В
вершинах на оси
имеем
.
Из (1.2.24) следует, что в них
.
§3. Круговое движение точки
В этом параграфе на примере кругового движения точки будем рассматривать задание ее движения различными способами.
Круговое движение является частным случаем плоского движения точки.