В.ВЕКЕРИК, Д.ІЛЬЧИШИНА,

К.ЛЕВЧУК, І.ЦІДИЛО, Л.ШАЛЬДА

ТЕОРЕТИЧНА

МЕХАНІКА

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ

“КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ”

ІВАНО-ФРАКІВСЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ НАФТИ І ГАЗУ

В.І.Векерик, Д.І.Ільчишина, К.Г.Левчук, І.В.Цідило, Л.М.Шальда

ТЕОРЕТИЧНА МЕХАНІКА

Рекомендовано

Міністерством освіти і науки України

як навчальний посібник для студентів

вищих навчальних закладів

№ 14/18.2-304 від 09.02.05

Івано-Франківськ

2006

ББК 22.21.73

УДК 531.8

В.І.Векерик, Д.І.Ільчишина, К.Г.Левчук, І.В.Цідило, Л.М.Шальда

Теоретична механіка. Навч. посібник. – Івано-Франківськ. Факел, 2006. – с

ISBN 966-694-047-7

В навчальному посібнику в стислій і доступній формі викладено основні положення теоретичної механіки: статики, кінематики, динаміки. Розглянуті елементи аналітичної механіки, теорії малих коливань системи в околі положення стійкої рівноваги.

У відповідності з вимогами положень Болонського процесу для самостійної роботи студентів наведено приклади і розрахунково-графічні роботи із застосуванням комп’ютера та методики їх розв’язування з основних тем курсу.

Викладені питання відповідають діючій навчальній програмі з теоретичної механіки для вищих технічних навчальних закладів III і IV рівнів акредитації.

Видання рекомендовано студентам денної та дистанційної форм навчання для самостійного вивчення курсу теоретичної механіки.

Рецензенти:

Факел, 2006

ЗМІСТ

	ПЕРЕДМОВА…………………….…………………	3
	ВСТУП………………………………………………	6
РОЗДІЛ 1 ГЕОМЕТРИЧНА СТАТИКА………..………		7
1.1	Основні поняття та закони………………………….	7
1.1.1	Рух матеріальної точки. Перший закон Ньютона. Основні властивості механічних сил………………	7
1.1.2	Означення статики………………………………….	10
1.1.3	Механічні в’язі та їхні реакції………………………	10
1.1.4	Аксіоми про в’язі та їхні реакції……………………	21
1.1.5	Класифікація сил. Метод перерізів…………………	22
1.1.6	Теорема про рівновагу трьох непаралельних сил, прикладених до твердого тіла………………………	23
1.1.7	Сили тертя ковзання і їхні властивості…………….	25
	Задачі для самостійного розв’язування…………….	29
	Запитання для самоконтролю…………………………	30
1.2	Основні властивості систем сил, прикладених до абсолютно твердого тіла……………………………	31
1.2.1	Аналітичне визначення ковзного вектора. Момент сили відносно точки і осі……………………………	31
1.2.2	Система збіжних сил. Умови рівноваги……………	35
	Задачі для самостійного розв’язування………………	38
1.2.3	Аналітичне визначення ковзного вектора рівнодійної системи двох паралельних сил. Центр паралельних сил……………………………………………	40
1.2.4	Пара сил. Момент пари сил. Властивості пари сил.	43
	Запитання для самоконтролю………………..………	45
1.3	Перетворення системи сил. Умови рівноваги…….	46
1.3.1	Аналітичне визначення головного вектора і головного моменту системи сил…………………………	46
1.3.2	Умови рівноваги вільного твердого тіла………….	48
1.3.3	Зведення систем сил до найпростішого вигляду. Інваріанти системи сил відносно центра зведення….	64
1.3.4	Центр паралельних сил і центр ваги……………….	68
	Запитання для самоконтролю…………………………	73
1.4	Розрахунково-графічна робота із застосуванням комп’ютера “Розрахунок плоскої ферми”…………	74
	Завдання на розрахунково-графічну роботу………	74
РОЗДІЛ 2 КІНЕМАТИКА………………………………..		99
2.1	Кінематика матеріальної точки…………………….	99
2.1.1	Основні положення………………………………….	99
2.1.2	Способи визначення руху точки……………………	99
2.1.3	Годограф векторної функції………………………..	103
2.1.4	Швидкість руху точки……………………………….	105
2.1.5	Прискорення руху точки……………………………	108
	Запитання для самоконтролю…………………………	116
2.2	Основи кінематики твердого тіла………………….	117
2.2.1	Основні положення………………………………….	117
2.2.2	Поступальний рух твердого тіла……………………	117
2.2.3	Обертальний рух твердого тіла навколо нерухомої осі…………………………………………………….	118
2.2.4	Вектори кутової швидкості і кутового прискорення. Формула Ейлера………………………………….	121
2.2.5	Рух вільного твердого тіла. Розподіл швидкостей і прискорень точок у вільному твердому тілі………	124
	Задачі для самостійного розв’язування………………	130
	Запитання для самоконтролю…………………………	131
2.2.6	Плоскопаралельний рух твердого тіла. Рівняння руху……………………………………………………	131
2.2.7	Розподіл швидкостей точок тіла при плоскопаралельному русі……………………………………………	134
2.2.8	План швидкостей……………………………………	138
2.2.9	Розподіл прискорень точок при плоскопаралельному русі ………….……………………………………	141
2.2.10	Миттєвий центр прискорень……………………….	143
	Задачі для самостійного розв’язування………………	149
	Запитання для самоконтролю…………………………	150
2.2.11	Додавання обертальних рухів навколо осей, що перетинаються………………………………………….	150
2.2.12	Рух твердого тіла навколо нерухомої точки. Аксоїди. Теореми Пуансо………………………………….	153
2.2.13	Теорема Ейлера. Кути Ейлера. Рівняння руху твердого тіла з нерухомою точкою ……………………	154
2.2.14	Розподіл швидкостей і прискорень точок тіла з нерухомою точкою…………………………………….	158
	Задачі для самостійного розв’язування …………….	162
	Запитання для самоконтролю………………………….	163
2.3	Складний рух матеріальної точки…………………..	163
2.3.1	Основні положення…………………………………..	163
2.3.2	Теорема про додавання швидкостей точки…………	165
2.3.3	Теорема про додавання прискорень точки…………	166
	Задачі для самостійного розв’язування………………	171
2.4	Складний рух твердого тіла…………………………	173
2.4.1	Додавання поступальних рухів тіла………………..	173
2.4.2	Пара обертань……………………………………..…	174
2.4.3	Додавання обертань тіла навколо паралельних осей……………………………………………………	176
2.4.4	Додавання поступального і обертального рухів тіла	178
2.4.5	Метод “зупинки” (метод Вілліса)…………………..	180
	Задачі для самостійного розв’язування………………	186
2.5	Розрахунково-графічна робота із застосуванням комп’ютера “Кінематика багатоланкового механізму”	192
2.6	Знайти положення миттєвих центрів прискорень….	235
РОЗДІЛ 3 ДИНАМІКА……………………………………		237
3.1	Динаміка матеріальної точки……………………….	237
3.1.1	Диференціальні рівняння руху вільної матеріальної точки. Основні задачі динаміки точки……………..	237
3.1.2	Прямолінійні коливання точки……………………..	246
	Задачі для самостійного розв’язування………………	258
	Запитання для самоконтролю…………………………	259
3.2	Динаміка системи матеріальних точок…………….	260
3.2.1	Основні поняття………………………………………	260
3.2.2	Диференціальні рівняння руху невільної системи.	264
3.2.3	Принцип Даламбера…………………………………	265
3.2.4	Динаміка відносного руху точки……………………	272
	Задачі для самостійного розв’язування………………	279
	Запитання для самоконтролю…………………………	281
3.3	Основні теореми динаміки………………………….	282
3.3.1	Теорема про зміну кінетичної енергії точки………	282
3.3.2	Елементи теорії потенціального силового поля. Закон збереження повної механічної енергії ………..	290
3.3.3	Теорема про зміну кінетичної енергії матеріальної системи………………………………………………	294
3.3.4	Обчислення моментів інерції………………………	303
3.3.5	Теорема про рух центра мас системи………………	308
3.3.6	Теореми про зміну кількості руху системи і зміну кінетичного моменту………………………………..	309
	Задачі для самостійного розв’язування………………	324
	Запитання для самоконтролю…………………………	327
3.4	Елементи теорії удару……………………………….	329
3.5	Розрахунково-графічна робота із застосуванням комп’ютера…………………………………………..	348
РОЗДІЛ 4 ЕЛЕМЕНТИ АНАЛІТИЧНОЇ МЕХАНІКИ..		356
4.1	Диференціальні принципи механіки………………..	356
4.1.1	Основні положення………………………………….	356
4.1.2	Принцип можливих переміщень. Загальне рівняння статики……………………………………………….	358
4.1.3	Принцип Даламбера-Лагранжа. Загальне рівняння динаміки ………………………………………………	362
	Запитання для самостійного розв’язування..………	365
	Запитання для самоконтролю…………………………	367
4.2	Рівняння рівноваги і руху матеріальної системи в узагальнених координатах…………………………..	367
4.2.1	Узагальнені координати, узагальнені швидкості, узагальнені сили……………………………………..	367
4.2.2	Загальне рівняння статики в узагальнених координатах. Узагальнені рівняння рівноваги……………	371
4.2.3	Рівняння Лагранжа другого роду ..…………………	372
4.2.4	Методика застосування рівнянь Лагранжа другого роду……………………………………………………	373
4.2.5	Рух системи в консервативному полі. Кінетичний потенціал…………………………………………….	377
4.2.6	Рівняння Лагранжа другого роду для дисипативних систем. Функція Релея..……………………………..	379
4.2.7	Кінетична енергія і функції Релея в узагальнених координатах……………….…………………………	381
4.2.8	Узагальнене рівняння енергії. Фізичний зміст функцій Релея……………………………………….……	383
	Запитання для самостійного розв’язування….……	387
	Запитання для самоконтролю…………………………	388
4.3	Малі коливання матеріальної системи…………….	388
4.3.1	Положення стійкої рівноваги. Теорема Лагранжа-Діріхле. Теореми Ляпунова…..…………………….	388
4.3.2	Диференціальні рівняння малих коливань системи в околі положення стійкої рівноваги………………..	391
4.3.3	Вільні коливання системи з N степенями вільності .	393
4.3.4	Вільні коливання системи з одним степенем вільності. Інтерпретація руху на фазовій площині……..	396
4.3.5	Вплив сил опору на вільні коливання системи. Згасаючі коливання………………………………………	399
4.3.6	Вимушені коливання системи. Вплив сил опору на вимушені коливання.…………………………………	401
4.3.7	Дослідження амплітудно-частотних характеристик системи…………………………………………….…	404
	Запитання для самостійного розв’язування…………	412
	Запитання для самоконтролю…………………………	413
4.4	Розрахунково-графічні роботи із застосуванням комп’ютера....................................................................	414
	Список літератури…………………………………..	440
	Українсько-російський словник…………………	441
	Предметний покажчик…………………………….	446

Передмова

Розвиток теоретичних основ нової техніки незаперечно засвідчує: теоретична механіка актуальна і в наш час не тільки, як засіб поглибленої інформації про основні закони природи, на підставі яких створюють розрахункові схеми, необхідні в інженерній справі, але також як засіб виховання у майбутніх інженерів навичок щодо наукових узагальнень.

Це відбувається тому, що сама теоретична механіка в цілому і у своїх частинах є прикладом величезного наукового узагальнення, отриманого внаслідок кропіткої праці багатьох поколінь вчених.

Однією з ознак адаптації вищої школи до Болонського процесу є істотне скорочення аудиторних занять з усіх фундаментальних дисциплін, у тому числі з теоретичної механіки. Багато уваги приділяється самостійній роботі студентів.

З цим пов’язана необхідність створення підручника, придатного для самостійного вивчення теоретичної механіки. У технічних вузах теоретична механіка має подвійне значення:

• розвиває у студентів здібність логічно мислити, створювати математичні моделі досліджуваного процесу зі застосуванням комп’ютера;

• класична механіка дозволяє студентам ознайомитися з багатьма математичними методами, необхідними для проведення різноманітних інженерних розрахунків.

Запропонований посібник – це стислий виклад повного курсу „Теоретична механіка” без порушення його ідейної основи.

Перше видання посібника було надруковано майже 15 років тому невеликим накладом у 1000 екз. і мало назву "Теоретична механіка: Навч. посібник / Д.І.Ільчишина, Л.М.Шальда – К.: УМК ВО, 1991. – 252 с. Зазначимо, що методику викладання основних питань курсу, покладену в основу цього видання, розробляв протягом багатьох років роботи в КПІ і КДУ ім. Т. Шевченка академік АН УРСР М. О.Кільчевський.

Вже тоді підручник привернув до себе увагу освітян ще й тому, що у навчальних закладах України навчання розпочали проводити національною мовою.

З плином часу та бурним розвитком комп’ютеризації виникла нагальна потреба підручник оновити і доповнити, а також збільшити тиражування. В основу нового видання покладено лекції, розроблені в результаті плідної співпраці викладачів НТУУ „КПІ” і Івано-Франківського НТУ нафти і газу.

Зміст посібника апробовано в першому виданні (1991 р.). Він базується на знаннях, які отримані студентами при вивченні попередніх курсів, забезпечує наступність знань за спеціальністю і створює умови для використання технічних засобів, у тому числі комп’ютерної техніки для аналізу та виконання розрахунків, і служить базою для вивчення профілюючих дисциплін.

Автори зробили вагомий, необхідний для нашої освітянської діяльності крок в опрацюванні української технічної термінології таких дисципліни, як теоретична та прикладна механіка, опір матеріалів, теорія механізмів і машин, деталі машин.

У новому виданні посібника враховані науково-технічні досягнення та технології, нові методи відповідних розрахунків, що дає змогу студентам зосередитись на математичному моделюванні фізичних процесів, а громіздкі математичні розрахунки виконувати із застосуванням комп’ютерних пакетів Mathematica, Mathcad, Maple, Matlab. Кожний розділ закінчується прикладом розрахункової роботи, запозиченої з відомого російського підручника «Сборник курсовых работ по теоретической механике» под. общ. ред. проф. А.А.Яблонского, виконаної в середовищі Maple. Це дозволило продемонструвати, що з ускладненням завдань досліджень механічних процесів набули розвитку теорія математичного опису, методологія досліджень, застосування моделюючих і розрахункових пристроїв, комп’ютерні технології.

Курс "Теоретична механіка" є важливою дисципліною, яка викладається студентам, що навчаються за технічними спеціальностями у вищих навчальних закладах. Його створено авторами відповідно до типової програми дисципліни "Теоретична механіка".

Предметом вивчення дисципліни є вивчення рухів фізичних об’єктів та умов їхньої рівноваги, методи їх аналізу та розрахунку, орієнтовані на забезпечення практичних і лабораторних занять, завдань для розрахункових робіт та курсових проектів. Мета вивчення полягає в формуванні інженерного розуміння фізичної сутності роботи механізмів, вмінь та навичок її оцінювати; визначати та розрахувати основні кінематичні та динамічні характеристики для керування процесами і режимами, спроможності передбачати хід і розвиток цих процесів.

Посібник складається із передмови, вступу і чотирьох частин: статика, кінематика, динаміка і аналітична механіка. Структура розташування параграфів відповідає програмі дисципліни і загальноприйнятій схемі викладання курсу. Спочатку подані загальні відомості про предмет, означення, а далі – теорія і практичні методи їх аналізу, орієнтування студентів на самостійну роботу. Така побудова дозволяє студентам краще розуміти фізику процесів і явищ, які виникають в механізмах при їх роботі, та полегшує вивчення дисципліни.

Викладення статики спирається на теорію ковзних векторів. Це дає змогу викладати курс традиційним методом при досить істотному скороченні аудиторного часу на її викладення.

Крім того, у розділі „Динаміка” основні положення і рівняння рівноваги статики розглянуті як окремий випадок основних теорем динаміки, що зручно для односеместрових курсів.

Посібник структурований з погляду на необхідність забезпечити студентам ясне бачення послідовності й зв’язків нових знань, що вони вивчають. У тексті використано різні форми виділення нових навчальних елементів, понять, термінів, змістовних модулів, що сприяє поліпшенню засвоєння матеріалу, поліпшенню наочності та швидкому пошуку. Органічною складовою подання нових знань є приклади розв’язування задач, що піднімають інформативність матеріалу з навчальною метою.

Усі розділи завершуються контрольними запитаннями по теоретичному курсу, методичними складовими, що спрямовують самостійну роботу студентів над навчальним матеріалом, і задачами для самостійного розв’язування. У кінці посібника додано список літератури, з якої використано фактичний матеріал.

Мета посібника – дати можливість студентам отримати знання та вміння для проектування механічних систем, засвоїти методи аналізу та методологію розрахунків для проведення наукових досліджень, оскільки підручники були і залишаються невід’ємним елементом навчання за освітньо-професійними програмами бакалавра, спеціаліста, магістра.

Компоновка підручника, послідовність викладання, теоретичні обґрунтування основних положень, що підкріплені великою кількістю прикладів з їх розв’язками, створюють необхідні передумови для успішного засвоєння матеріалу студентами.

Вступ

Механіка – це природнича наука, яка вивчає найпростіші рухи матерії – механічні.

Найпростіші форми рухів – це прості переходи фізичних тіл з одного положення у просторі і часі в інше, тому механіка є однією з природничих наук.

Вивчаючи найзагальніші властивості рухів, механіка не враховує більшість конкретних властивостей фізичних тіл. Вона спирається лише на первісні властивості речовин; такі, як її протяжність і властивість частинок тяжіти одна до одної, тобто мати певну вагу. Зрозуміло, що в механіці користуються низкою спрощених (абстрактних) уявлень. В її основу покладено такі поняття, як матеріальна точка, система матеріальних точок та абсолютно тверде тіло.

Поняття про матеріальну точку є однією з граничних абстракцій, яка виникла внаслідок спостережень за рухами тіл скінченних розмірів.

Матеріальною точкою називають тіло, розмірами якого можна знехтувати при розв’язанні певних задач механіки.

Системою матеріальних точок називають сукупність матеріальних точок, рухи й положення яких взаємопов’язані. Незмінною системою матеріальних точок називають систему, точки якої не змінюють взаємного положення протягом часу.

Якщо точки суцільно заповнюють частину простору, який займає незмінна матеріальна система, то останню називають абсолютно твердим тілом.

Основна властивість абсолютно твердого тіла полягає у незмінності відстані між будь-якими двома точками під час руху.

Поняття про абсолютно тверде тіло є граничною абстракцією.

Таким чином,

теоретичною механікою називають ту частину загальної механіки, яка вивчає рух матеріальних точок, систем матеріальних точок та абсолютно твердих тіл.

Розглядаючи граничні абстракції, теоретична механіка вивчає найзагальніші закони механіки, які справедливі для всієї механіки.

Теоретична механіка побудована за планом точних наук: в її основі лежить система означень та аксіом, на які, в свою чергу, спираються доведення теорем.

РОЗДІЛ 1

ГЕОМЕТРИЧНА СТАТИКА

1.1. Основні поняття та закони

1.1.1. Рух матеріальної точки. Перший закон Ньютона.

Основні властивості механічних сил

Основні поняття класичної механіки вперше були сформульовані І. Ньютоном, який розглядав рух вільної матеріальної точки, тобто такої, на рух якої заздалегідь не накладені будь-які обмеження, які не залежать від подальшого закону руху.

Перший закон І. Ньютона (закон інерції) стверджує, що ізольована матеріальна точка зберігає стан рівномірного і прямолінійного руху або перебуває у стані спокою відносно системи координат, яка рухається поступально, рівномірно і прямолінійно.

Вважається, що ця система координат рухається відносно нерухомої системи координат. Наявність абсолютно нерухомої системи координат є однією з основ, на якій ґрунтується класична механіка.

Якщо рух точки відрізняється від рівномірного і прямолінійного, то це означає, що на точку діють будь-які зовнішні фактори.

Причину, внаслідок якої матеріальна точка змінює свій рух, називають механічною силою.

Переважна більшість рухів точок на Землі відрізняється від рівномірного й прямолінійного. Тому поняття ізольованої матеріальної точки є граничною абстракцією. Точки матеріальної системи завжди перебувають під взаємним впливом. Якщо будь-який рух переноситься з одного тіла на інше, то він активний і його можна розглядати як причину руху.

Отже, механічна сила є рух, який у механічній формі передається від одного тіла до іншого при їхній взаємодії.

Кожна сила має величину, напрям у просторі і точку прикладання.

Поняття механічної сили стійко прижилося в процесі еволюції науки, оскільки механічну силу можна кількісно виміряти й записати як функцію часу, координат точок простору та їхніх похідних за часом, тобто знайти її аналітичне визначення.

Сили зображають напрямленими відрізками прямих. Пряму, вздовж якої відкладають відрізок, що зображає силу, називають лінією дії сили.

Сформулюємо основні означення та аксіоми щодо механічних сил.

Означення 1. Зрівноваженою системою сил, або системою, еквівалентною нулеві, називають таку, під дією якої точка рухається рівномірно і прямолінійно або перебуває у стані спокою.

Означення 2. Матеріальна точка знаходиться у стані статичної рівноваги, якщо вона перебуває під дією зрівноваженої системи сил.

Означення 3. Матеріальна система знаходиться у стані статичної рівноваги, якщо кожна її точка перебуває у стані рівноваги.

Відповідно до цих означень зауважимо, що рух матеріальної системи не зміниться, якщо до її точок прикладати або від неї віднімати зрівноважену систему сил.

Означення 4. Дві системи сил називають статично еквівалентними, якщо кожна з них окремо зрівноважує одну й ту саму третю систему сил.

Означення 5. Рівнодійною системи сил називають силу, еквівалентну системі сил. Силу, що зрівноважує систему сил, називають зрівноважуючою.

І. Ньютон у додаткових зауваженнях до основних законів механіки аксіоматично сформулював правило паралелограма сил, яке дістало назву аксіоми про паралелограм сил.

Якщо на матеріальну точку діють дві сили, то їхню дію можна замінити дією однієї сили – їм рівнодійної, яка визначається діагоналлю паралелограма, побудованого на цих силах.

Ця аксіома формулює правило векторного додавання сил.

Відтепер можна вважати механічні сили векторами.

У механіці розглядають вектори трьох типів: означені, або прикладені, ковзні та вільні.

Означений вектор, наприклад, вектор сили, що діє на точку, характеризується трьома його проекціями на всі осі координат і координатами точки його прикладання, тобто шістьма параметрами.

Ковзний вектор можна переносити вздовж лінії його дії. Тому він визначається п’ятьма параметрами, оскільки три координати точки прикладання вектора зв’язані системою двох рівнянь, які визначають лінію дії вектора у просторі.

Нарешті, для визначення вільного вектора потрібно знати лише три його проекції.

Аксіома про абсолютно тверде тіло.

Якщо тверде тіло перебуває у рівновазі під дією двох сил, то ці сили протилежні за напрямом, однакові за величиною і мають спільну лінію дії.

Зрівноважену систему сил і , яка діє на абсолютно тверде тіло, зображено на рис. 1.1.

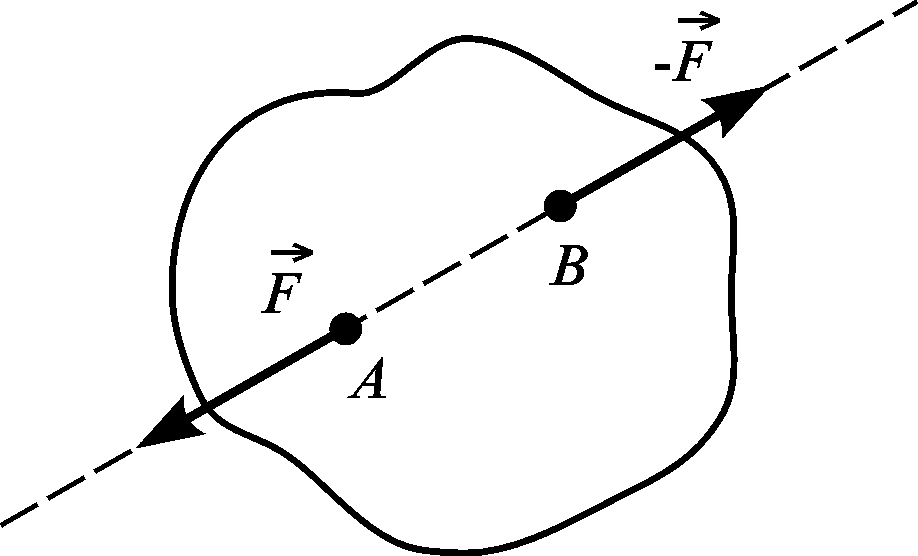
Теорема. Стан механічного руху тіла не зміниться, якщо силу перемістити вздовж лінії її дії у будь-яку точку.

^* Нехай на тіло (рис. 1.2) діє сила , прикладена в точці . Стан механічного руху тіла не зміниться, якщо в довільній точці , розташованій на лінії дії сили , прикласти зрівноважену систему сил і (модулі сил однакові і дорівнюють модулю сили, прикладеної в точці ). На підставі попередніх означень та аксіоми про абсолютно тверде тіло можна вважати силу , прикладену в точці , і , прикладену в точці , зрівноваженими і відкинути; залишилася сила , прикладена в точці .

Рисунок 1.1

Рисунок 1.2

Отже, на підставі доведеної теореми, вектор сили, прикладеної до абсолютно твердого тіла, можна вважати ковзним.