Умови рівноваги довільної системи сил

З результатів приведення довільної системи сил до головного вектора і головного момента ми бачимо, що тверде тіло перебу­ватиме у рівновазі лише тоді, коли і головний вектор , і голов­ний момент системи дорівнюватимуть нулеві, тобто

(1.30)

Проектуючи ці рівності на декартові осі координат, запишемо аналітичні умови рівноваги довільної просторової си­стеми сил у вигляді шести рівнянь (відповідно до шести степеней вільності тіла у просторі):

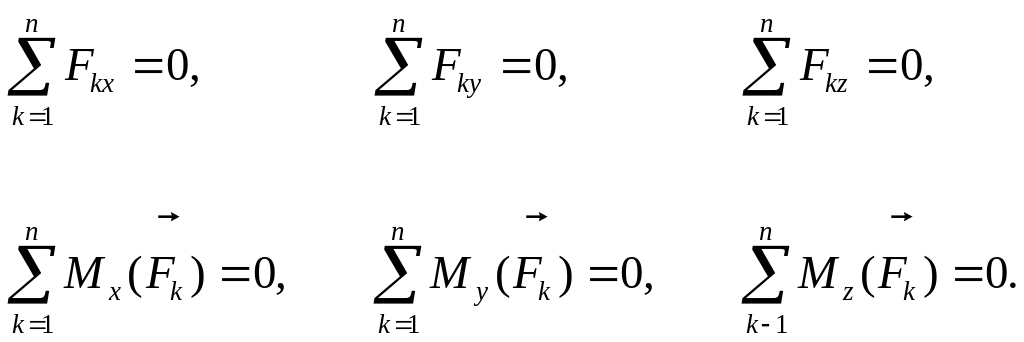(1.31)

Тут - проекції сил на координатні осі, - моменти сил відносно цих осей.

Ці умови читаються так: для рівноваги довільної просторо­вої системи сил необхідно і достатньо, щоб алгебраїчні суми проекцій всіх сил на три взаємно перпендикулярні осі дорівню­вали нулю і суми моментів усіх сил відносно цих осей дорівню­вали нулю.

Якщо всі сили довільної системи діють в одній площині, то аналітичні умови рівноваги довільної плоскої системи сил зводяться до запису трьох рівнянь (відповідно до трьох степенів вільності тіла на площині):

. (1.32)

Тут - момент всіх сил відносно осі Оz, котра пер­пендикулярна до площини Оху, в якій діють сили, і може бути проведена із будь-якої точки площини. А тому цей вираз ми можемо замінити визначенням суми моментів усіх сил відносно будь-якої точки площини. При розв'язуванні задач статики за таку точку (центр моментів) потрібно вибирати ту точку пло­щини, через яку проходять лінії дії найбільшої кількості невідо­мих сил чи реакцій в'язей - це спрощує розв'язок системи рів­нянь.

Таким чином, для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб алгебраїчна сума проекцій всіх сил на дві взаємно перпендикулярні осі дорівнювала нулю і алге­браїчна сума моментів усіх сил відносно будь-якої точки пло­щини дорівнювала нулю.

Відзначимо, що рівняння рівноваги (1.32) плоскої довільної системи сил можна подати у різній формі, а саме: можна скласти два рівняння моментів відносно двох будь-яких точок А і В та одне рівняння проекцій сил на вісь

, (1.33)

можна скласти три рівняння моментів відносно трьох точок, які не лежать на одній прямій

. (1.34)

Іноді доводиться розв'язувати задачі на рівновагу складних конструкцій - системи кількох тіл. У таких випадках засто­совується метод перерізів у точках з'єднання тіл, який дозво­ляє розглядати рівновагу кожного окремого тіла системи, відки­нувши при цьому всі інші тіла і замінивши їх дію реакціями тих в'язей, які з'єднують ці тіла.

Рівновага при наявності сил тертя

Із досвіду ми знаємо, що при спробі рухати одне тіло по поверхні другого в площині їх дотику виникає сила опору цьому рухові.

Припущення про в'язь у вигляді ідеально гладенької поверхні, яке ми розглядали раніше (див. "Типи в'язей") не відповідає реальній дійсності, тому що навіть при найретельнішій обробці контактуючих поверхонь залишається деяка шорсткість, яка обумовлює силу опору при відносному русі одного тіла по по­верхні іншого. Цю силу називають силою тертя ковзання (або сухим тертям).

Тертя ковзання вперше експериментально вивчав французський фізик Амонтон (1663-1705), який довів, що сила тертя у досить широких границях не залежить від площі контакту­ючих поверхонь. Закони тертя були сформульовані майже через сто років пізніше Кулоном (1736-1806) і тому тертя ковзання часто називають кулоновим.

Припущення про абсолютну твердість тіл у теоретичній ме­ханіці також не відповідає дійсності, оскільки досвід показує, що при контакті рухомих тіл (наприклад, при коченні колеса по дорозі) виникає опір цьому рухові, який називають тертям ко­чення.

Близьке по природі як до тертя ковзання, так і до тертя ко­чення, є тертя крутіння (або вертіння), яке виникає при загвин­чуванні, свердлінні і являє собою досить складний процес.

Вивчення рівноваги тіл з урахуванням сил опору звичайно зводиться до розгляду граничного положення рівноваги, коли сили тертя досягають свого найбільшого значення.