Момент сили відносно осі

Якщо момент сили відносно деякого центра О викликає обертальний рух тіла навколо цього центра, то момент сили відносно осі викликає, зрозуміло, обертання тіла навколо даної осі. При цьому задача визначення плеча сили відносно осі дещо складніша, ніж визначення плеча сили відносно точки, але врешті решт зводиться до останнього. Пояснимо це на прикладі (рис. 1.21).

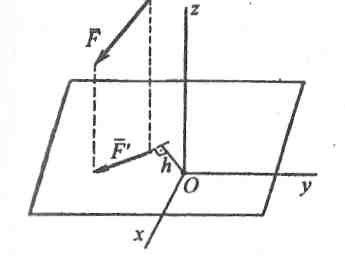
Рис. 1.21.

Щоб знайти плече сили відносно осі Оz, спроектуємо силу на площину Оху, пер­пендикулярну до осі Оz, а саму вісь Оz також спроектовуємо на цю ж площину. В резуль­таті одержимо проекцію сили і точку О (початок коор­динат). А далі з точки О опус­каємо перпендикуляр на лінію дії проекції сили . Це й буде шукане нами плече сили від­носно осі.

Модуль момента сили відносно осі знайдемо як добуток мо­дуля проекції сили на плече h:

. (1.24)

Знак момента визначається, як і раніше, в залежності від на­пряму обертання тіла навколо осі під дією даної сили: якщо обер­тання здійснюється проти годинникової стрілки - знак "плюс", якщо за стрілкою - "мінус".

Таким чином, момент сили відносно осі дорівнює добутку проекції сили на площину, яка перпендикулярна до даної осі, на плече. Плечем є перпендикуляр, опущений з початку коорди­нат на лінію дії проекції сили.

При достатніх практичних навиках розв'язування задач операцію проектування сил на ту чи іншу площину можна проминути завдяки просторовій уяві, яку свого часу мав дати студен­там курс нарисної геометрії.

Момент сили відносно осі дорівнює нулю у двох випадках:

1. якщо сила паралельна осі (проекція сили );

2. якщо сила перетинає вісь (плече h = 0).

Довільна система сил. Приведення до одного центра

Довільною системою сил називається сукупність прикладе­них до твердого тіла сил, лінії дії яких орієнтовані довільно у просторі.

Розглядаючи збіжну систему сил, ми переконалися, що цю систему можна замінити однією рівнодійною силою, яка дорів­нює векторній сумі всіх сил, що входять у систему.

Систему паралельних сил також можна привести або до рівнодійної сили, або до пари сил.

Спробуємо спростити прикладену до абсолютно твердого тіла довільну систему сил, привівши всі сили до одного заданого центра О (рис. 1.22). Почнемо з сили перенісши її паралельно самій собі у точку О і позначивши перенесену силу . Однак, щоб стан тіла при цьому не змінився, прикладемо у точці О силу , яка урівноважить силу . Дві паралельні, рівні за модулем і протилежні за напрямом сили і ми можемо трактувати як пару сил ( , ), а силу , прикладену в точці О, - як перенесену в точку О силу .

Повторивши аналогічну операцію переносу до центра О cил одержимо пучок сил прикладених у точці О (збіжну систему сил), і систему пар сил з моментами , яку отримали внаслідок проведених операцій переносу. Векторна сума всіх збіжних сил дасть рівнодійну або так званий головний вектор системи, прикладений у точці О, а векторна сума моментів всіх приєдна­них нар сил дасть головний момент системи .

Таким чином, довільну систему сил можна звести до од­нієї рівнодійної сили (головного вектора), прикладеній у цен­трі приведення і рівній векторній сумі всіх сил системи, та до однієї пари сил (головного моменти) з моментом рівним векторній сумі моментів усіх приєднаних пар:

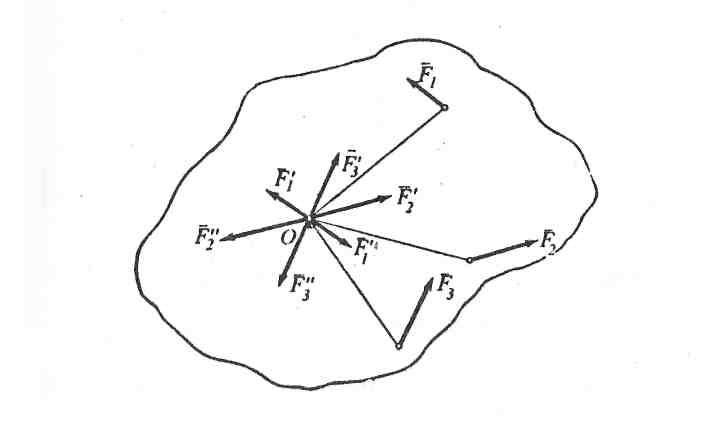
Рис. 1.22.

. (1.25)

Головний момент системи приєднаних пар сил можна роз­глядати і як векторну суму моментів всіх вихідних сил відносно центра О:

. (1.26)

Модулі векторів і визначаються з формул

. (1.27)

З'ясуємо тепер, як позначиться на головному векторі і го­ловному моменті зміна положення центра приведення довільної системи сил.

Цілком очевидно, що головний вектор не залежить від по­ложення центра приведення, а головний момент буде залежати, тому що зміняться плечі сил. При цьому головний момент сил відносно нового центра приведення зміниться на величину, рівну моменту попереднього головного вектора системи відносно но­вого центра:

. (1.28)

Тут і - головні моменти даної системи сил відносно попереднього центра О і нового центра О_{1 ,} а - момент головного вектора відносно нового центра приведення, який визначається за формулою

. (1.29)

При приведенні довільної системи сил до заданого центра можуть мати місце такі випадки:

1. головний вектор ,а головний момент (під дією такої системи сил тіло рухається поступально);

2. головний вектор , а головний момент (під дією такої системи тіло обертається);

3. головний вектор і головний момент (під дією такої системи сил тіло знаходиться у рівновазі);

4. головний вектор і головний момент , при­чому можуть бути такі три окремі випадки: ; і утворює кут з вектором (під дією такої системи сил тіло здійснює складний рух, який зводиться або до так званого силового гвинта, або до плоско-паралельного руху).