Моменти інерції

При визначенні кінетичної енергії тіл, що обертаються, ми зустрілись із новою фізичною величиною, яка називається мо­ментом інерції тіла. Поняття момента інерції було введене Леонардом Ейлером. Слід зауважити, що якщо маса тіл є мірою їх інертності при поступальному русі, то мірою інертності тіл при обертанні є момент інерції (або момент інертності).

Моментом інерції тіла називається скалярна величина, яка характеризує розподіл маси в тілі (або в системі тіл) і є мірою інертності при обертальному русі.

Розрізняють слідуючі моменти інерції:

1. полярний ;

2. осьові ;

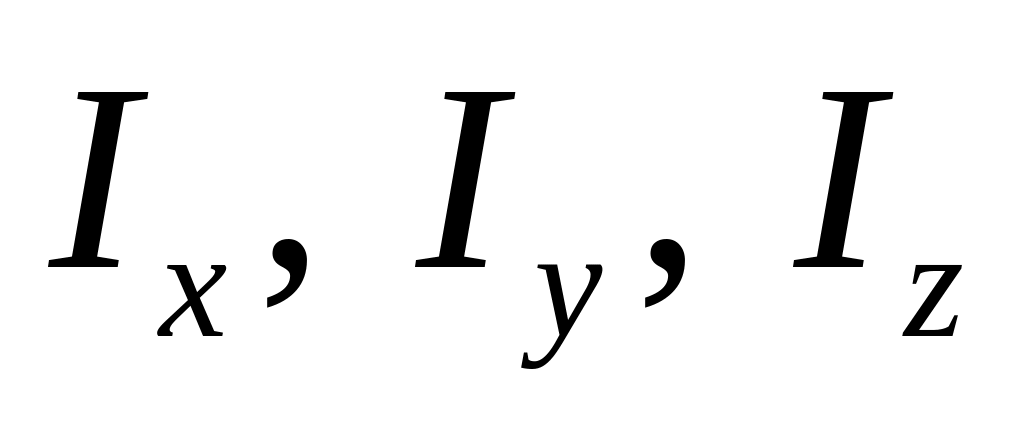3. відцентрові .

Для визначення полярного момента інерції розглянемо будь-яку -ту точку тіла з масою і радіусом-вектором . Момент інерції -ої точки відносно центра О дорівнює добутку маси точки на квадрат відстані від цього центра

. (3.87)

Оскільки

, (3.88)

то

. (3.89)

Підсумовуючи для всіх точок тіла , маємо

, або . (3.90)

Таким чином, за формулою (3.90), полярний момент інерції дорівнює сумі добутків маси кожної точки тіла на квадрат її відстані до полюса (початку координат).

Осьові (або аксіальні) моменти інерції визначаються для кож­ної -ої точки тіла як добуток маси точки на квадрат її відстаю від даної осі. Наприклад, осьовий момент інерції точки відносно осі дорівнює

. (3.91)

Відстань точки від осі виражається через координати точки

. (3.92)

Отже

. (3.93)

Підсумувавши для всіх точок тіла, маємо

. (3.94)

Аналогічно можемо записати вирази для і :

. (3.95)

Осьовий момент інерції тіла дорівнює сумі добутків маси кож­ної точки на квадрат її відстані до осі.

Якщо складемо всі три осьові моменти інерції (3.94) і (3.95), то одержимо

, (3.96)

або

. (3.97)

Отже, сума осьових моментів інерції тіла дорівнює подвоє­ному полярному моменту, взятому відносно початку координат.

Відцентровими моментами інерції називають величини, які дорівнюють алгебраїчній сумі добутків маси кожної точки тіла на добуток її відповідних координат:

. (3.98)

Якщо відносно деякої системи координат, вибраної в тілі, відцен­трові моменти інерції дорівнюють нулю, то осі такої системи називають головними осями інерції. Якщо ж початок такої си­стеми координат співпадає з центром мас тіла (чи системи), то такі осі називають головними центральними осями інерції.

Момент інерції тіла відносно заданої осі можна представити як добуток маси тіла на квадрат деякої умовної лінійної вели­чини, яка являє собою відстань центра мас тіла до даної осі і називається радіусом інерції тіла:

. (3.99)

Тут - маса тіла, - радіус інерції тіла відносно осі . Радіус інерції знаходиться із формули

(3.100)

і може бути визначений експериментально.

Осьові моменти інерції тіл простої форми

Дуже часто при розв'язуванні задач про обертальний рух необхідно мати осьові моменти інерції однорідних тіл простої форми. Розглянемо деякі з них:

1. Тонкий однорідний стержень

М омент інерції однорідного стержня довжиною відносно осі , що перпендикулярна до стержня і проходить через його кінець (рис. 3.8), визначається як сума добутків маси кожної окремої -ої частинки стержня на квадрат відстані від осі

Рис. 3.8.

. (3.101)

де - відстань від -ої точки до осі. Однак у випадку неперервного розподілу маси в стержні замість суми застосує інтеграл поширений по всій масі стержня

. (3.102)

Тут dm - маса елемента стержня довжиною dx , х - відстань елемента від осі .

Оскільки елементарна маса , то підставивши цей вираз у (3.102), маємо

,

звідки

. (3.103)

Отже, момент інерції тонкого однорідного стержня відносно осі, що перпендикулярна до стержня на його кінці, дорівнює третині добутку маси на квадрат довжини стержня.

Якщо нам потрібний момент інерції однорідного стержня відносно осі, що проходить через його середину (центр мас С), то маємо

, (3.104)

звідки

. (3.105)

2. Однорідне тонке кільце (обруч)

Нехтуючи товщиною кільця радіуса R, знайдемо його момент інерції відносно центральної осі . Для цього виділимо в кільці елемент маси dm (рис. 3.9). Тоді

, (3.106)

або

. (3.107)

Рис. 3.9.

Отже, момент інерції однорідного тонкого кільця (обруча) відносно осі дорівнює добутку маси кільця на квадрат його радіуса.

Оскільки товщиною кільця знехтувано, то неважко побачити, що , де - полярний момент інерції кільця відносно його центра. Через те, що кільце симетричне, моменти інерції від­носно двох інших (поперечних) осей рівні . Викори­ставши залежність між полярним і осьовими моментами інерції, запишемо

,

звідки

.

Отже

, (3.108)

тобто моменти інерції кільця відносно поперечних осей Ох та Оу дорівнюють половині момента інерції .

3. Однорідний суцільний диск

Я кщо радіус диска ,то момент інерції відносно центральної осі (рис. 3.10) визначимо з формули

Рис. 3.10.

, (3.109)

де dm - елементарне кільце диска тов­щиною dr, взяте на відстані r від осі. Маса цього елементарного кільця

.

Отже

,

звідки

. (3.110)

Таким чином, момент інерції суцільного однорідного диска відносно центральної осі дорівнює половині добутку маси диска на квадрат його радіуса.

Моменти інерції диска відносно осей Ох і Оу знаходяться аналогічно до відповідних моментів обруча і становлять поло­вину від , тобто

. (3.111)

4. Однорідний суцільний циліндр

Розіб'ємо циліндр, що має висоту h і радіус R, на елементарні диски товщиною dz (рис. 3.11). Маса кожного з цих дисків

, (3.112)

а момент інерції кожного елементар­ного диска відносно осі Ох визна­чається з формули

Рис. 3.11.

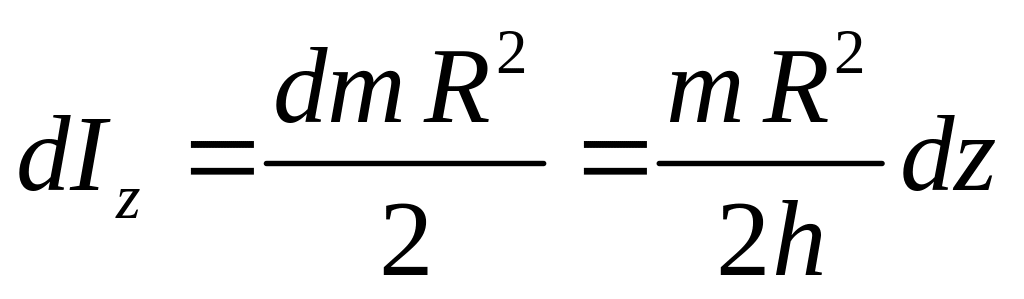. (3.113)

Інтегруючи по всій висоті, знайдемо

,

звідки

. (3.114)

Отже, момент інерції однорідного суцільного циліндра відносно поздовжньої осі не залежить від висоти циліндра і дорівнює половині добутку маси циліндра на квадрат його радіуса, тобто моменти інерції циліндра і тонкого диска відносно осі співпадають.