Робота внутрішніх сил системи

Внутрішні сили системи матеріальних точок - це сили взаємодії між точками, що входять до складу системи. У біль­шості випадків внутрішні сили являють собою реакції тих в'язей, які з'єднують точки системи і по закону рівності дії і протидії врівноважуються між собою.

Робота реакцій внутрішніх в’язей системи дорівнює нулю у тому випадку, коли в’язі є ідеальними. До таких в'язей нале­жать гнучкі невагомі та нерозтяжні нитки, поверхні і шарніри без тертя, ідеальні стержні тощо.

Робота внутрішніх сил системи дорівнює нулю і в тому ви­падку, коли в процесі руху відстані між точками системи не змінюються (так звані незмінні системи).

Отже, у більшості задач динаміки роботою внутрішніх сил нехтують:

.

Потужність сили

Потужність визначається роботою, виконаною силою за оди­ницю часу. Наприклад, якщо за час dt сила здійснила роботу , то вираз для потужності сили матиме вигляд

, (3.79)

або по модулю

, (3.80)

Отже, потужність сили є скалярною величиною, яка дорівнює добутку сили на швидкість точки її прикладання. Одиницею виміру потужності є ват (1 Вт = 1 Дж/с = 1 Н∙м/с).

Кінетична енергія твердого тіла

Кінетична енергія механічної системи, як ми встановили вище, дорівнює арифметичній сумі кінетичних енергій окремих тіл (точок) системи. Ці тіла можуть рухатись поступально, обертатись навколо нерухомої осі або здійснювати більш склад­ний плоско-паралельний рух. Розглянемо почергово ці три ви­падки руху.

1. Якщо тіло здійснює поступальний рух, то всі його точки (у тому числі і центр мас) мають однакові швидкості . Кіне­тична енергія обчислюється як сума кінетичних енергій всіх n точок тіла

, (3.81)

або

. (3.82)

Тут - маса тіла, - швидкість центра мас тіла.

Таким чином, кінетична енергія при поступальному русі тіла дорівнює половині добутку маси тіла на квадрат швид­кості його центра мас.

2. При обертанні тіла навколо нерухомої осі лінійні швид­кості окремих точок визначаються з формули Ейлера

, (3.83)

де - кутова швидкість обертання, - радіус -ої точки тіла.

Кінетична енергія визначається так:

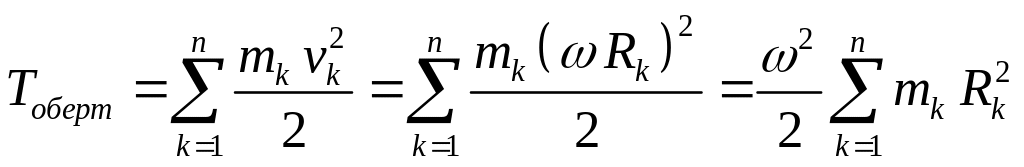, (3.84)

або

(3.85)

. (3.85)

Тут - момент інерції тіла відносно осі обертання, який дорівнює сумі добутків маси кожної точки на квадрат її відстані від осі.

Отже, при обертанні тіла навколо осі кінетична енергія дорівнює половині добутку момента інерції тіла відносно даної осі на квадрат кутової швидкості.

3. Одним і складних рухів тіла, які дуже часто зустріча­ються в механічних системах, є плоско-паралельний рух, прикла­дом якого є кочення колеса або циліндра по нерухомій площині без проковзування. Оскільки плоско-паралельний рух тіла можна розкласти на поступальний рух тіла разом з полюсом і миттєвий оберталь­ний рух навколо полюса, то вибравши за полюс центр мас тіла, можемо визначити кінетичну енергію як суму

. (3.86)

Отже, кінетична енергія тіла при плоско-паралельному русі дорівнює сумі кінетичної енергії поступального руху зі швид­кістю центра мас і кінетичної енергії при обертанні тіла на­вколо центра мас. Цей висновок у літературі часто навивають теоремою Кеніга. З її доведенням студенти можуть познайоми­тись у повних курсах теоретичної механіки.