Прямолінійні коливання точки. Вільні коливання

Прикладом розв'язування другої задачі динаміки у випадку, коли на точку діє активна сила, що є функцією переміщення буде визначення закону руху при прямолінійних коливаннях точки. Прямолінійні коливання виникають внаслідок дії поновлюючої сили пружності при стисканні чи розтягуванні таких пружних елементів, як пружина чи гума. Однак слід заува­жити, що пружні властивості в тій чи іншій мірі мають всі без винятку фізичні тіла і середовища, а тому коливання (вібрації) с одним із найбільш поширених у природі рухів.

Сила пружності направлена протилежно деформації (рис. 3.1). Модуль сили пружності /'пр пропорційний першій степені деформації

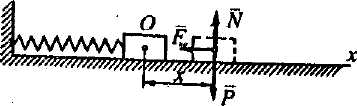
Рис. 3.1.

, (3.5)

де х - лінійна деформація пружного елементу, с - коефіцієнт пропорційності, який характеризує пружні якості елементу і називається коефіцієнтом пружності (або жорсткості). Ко­ефіцієнт пружності чисельно дорівнює силі, яку потрібно при­класти до пружного елементу для того, щоб змінити його довжину на одиницю виміру. Розмірність коефіцієнта пруж­ності в системі СІ - Н/м.

Диференціальне рівняння руху точки при проектуванні на вісь Ох має вигляд

або . (3.6)

Розділивши обидві частини рівності (3.6) на масу m, приве­демо це рівняння до вигляду, в якому воно відоме як стандартна форма диференціального рівняння вільних прямолінійних коливань точки

. (3.7)

Введена нами заміна має важливий фізичний зміст - це є частота вільних (власних) коливань.

Диференціальне рівняння (3.7) є лінійним однорідним рівнян­ням другого порядку. На жаль, воно не може бути розв'язане прямим інтегруванням і його розв'язок будемо шукати у вигляді

, (3.8)

де С - стала інтегрування, - невідомий параметр, який по­трібно визначити, t - час, e - основа натурального логарифма. Для визначення невідомого параметра підставимо розв'язок (3.8) і його другу похідну по часу у рівняння (3.7):

або

. (3.9)

Алгебраїчне рівняння (3.9) відносно , яке називають харак­теристичним рівнянням, дасть нам два корені

, (3.10)

а тому розв'язок (3.8) запишемо у вигляді суми двох доданків:

,

або

. (3.11)

Використавши підстановки Ейлера

,

одержимо нову форму запису розв'язку (3.11), якою, опуска­ючи всі проміжні викладки, користуються як кінцевою при розв'язуванні задач на вільні коливання точки:

, (3.12)

Тут і — сталі інтегрування, які визначаються о початко­вих умов руху точки.

Розв'язок (3.12) являє собою загальний інтеграл диферен­ціального рівняння (3.7). Продиференціювавши вираз (3.12), одержимо ще один інтеграл:

. (3.13)

Підставимо початкові умови руху ( = ) у (3.12) та (3.13) і визначимо сталі інтегруванні: .

З урахуванням значень і розв'язок рівняння (3.7) матиме вигляд

.

Розв'язок (3.12) можна звести до більш простої амплітудної форми такими замінами:

. (3.14)

Тут А і деякі сталі величини. Тоді (3.12) перепишеться у вигляді

,

або

. (3.15)

Із розв'язку (3.15) видно, що законом руху точки є гармонічна зміна координати , максимум якої є амплітудою вільних коливань, величина - це фаза коливань, - кругова частота, - початкова фаза.

Амплітуда коливань визначається через сталі інтегрування і піднесенням до квадрату виразів (3.14) і складанням їх:

,

звідки

. (3.16)

Початкову фазу також визначимо із (3.14) через сталі інтегрування:

,

звідки

. (3.17)

Період вільних коливань (час, що витрачається на одне повне коливання знаходиться за формулою

. (3.18)

Графіком вільних коливань є гармонічна функція (рис. 3.2). При цьому період і частота коливань залежать лише від маси точки і коефіцієнта пружності, а амплітуда і початкова фаза коливань залежать як від маси точки і коефіцієнта пружності, так і від початкових умов руху:

.

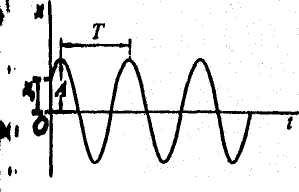
Рис. 3.2.