Абсолютне прискорення точки у складному русі

Для визначення абсолютного прискорення точки у складному русі запишемо формулу (2.103) о урахуванням у (2.98) і (2.100) такому вигляді

(2.104)

і візьмемо від нього похідну по часу:

(2.105)

Тут

- вектор абсолютного прискорення точки;

- вектор кутового прискорення рухомої системи (тіла або середовища).

Введемо такі значення для виразів у дужках формули (2.105):

- радіус-вектор точки в рухомій системі координат;

- відносна швидкість точки;

;

- відносне прискорення точки;

.

Як бачимо, весь великий вираз у правій частині формули (2.105) зводиться до п'яти доданків, два з яких однакові

,

або

. (2.106)

Перші два доданки правої частини цієї формули являють прискорення переносного руху, тобто прискорення тієї точки чи середовища, в якій в даний момент знаходиться рухома точка М:

. (2.107)

Останній доданок виразу (2.106) являє собою так зване поворотне або королісове прискорення

, (2.108)

а відтак і теорема про визначення абсолютного прискорення точки в складному русі називається теоремою Коріоліса на честь французького механіка, який вперше довів цю теорему:

. (2.109)

Теорема Коріоліса формулюється так; абсолютне прискорення точки в складному русі знаходиться як векторна сума переносного, відносного і коріолгсового прискорень.

Розглянемо більш детально переносне прискорення. Із формули (2.107) бачимо, що переносне прискорення складається із суми двох доданків та . Перший вектор являє собою переносне дотичне (або тангенціальне) прискорення, а другий - переносне нормальне прискорення:

, (2.110)

або по модулю

. (2.111)

Напрями прискорень і аналогічні розглянутим у розділі про обертання тіла навколо осі: вектор збігається з напрямом переносної швидкості при прискореному переносному обертання тіла і протилежний йому при сповільненому. Вектор направлений до центру обертання тіла.

Прискорення корюліса

Модуль прискорення Коріоліса знаходиться як модуль подвоєного векторного добутку двох векторів (див. формулу (2.108)):

. (2.112)

Як можна судити з формули (2.112), модуль коріолісового прискорення дорівнює нулю в трьох випадках:

1. (переносний рух тіла поступальний);

2. (точка в дану мить зупинилась);

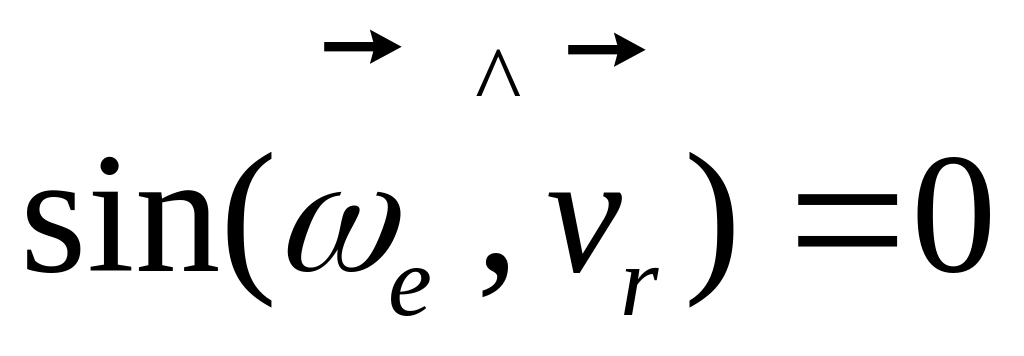3. (вектор паралельний вектору ).

Напрям вектора коріолісового прискорення визначається або згідно з правилом векторного добутку двох векторів, або за допомогою правила Жуковського.

Згідно з правилом векторного добутку з формули

(2.113)

бачимо, що вектор перпендикулярний до площини, яку створюють вектори і , і направлений у той бік, звідки поворот від першого вектора до другого вектора відбувається проти годинникової стрілки найкоротшим шляхом.

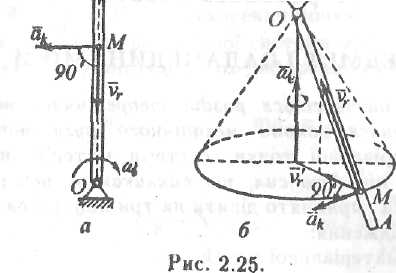
Згідно з правилом Жуковського, для визначення напряму прискорення Коріоліса потрібно повернути вектор на 90° у бік обертання тіла у випадку, коли вектор відносної швидкості точки перпендикулярний вектору кутової швидкості ) переносного руху тіла (див. рис. 2.24б і рис. 2.25а).

Рис. 2.24.

Якщо вектори і не перпендикулярні між собою, то потрібно спочатку спроектувати вектор на площину, перпендикулярну до вектора , а потім одержану проекцію повернути на у напрямі обертання тіла (див. рис. 2.24а і рис. 2.25б).