Складний рух точки

У розділі "кінематика точки" ми вивчали рух точки відносно декартової системи координат, яка безумовно вважалась неру­хомою. Однак у дійсності не існує абсолютно нерухомих систем відліку, а є лише умовно нерухомі, адже в природі все рухається, бо рух - це спосіб існування матерії.

У більшості технічних задач системи координат, зв'язані з Землею (так звані геоцентричні системи), вважаються нерухо­мими. Але ці ж системи в розрахунках, пов'язаних із косміч­ними польотами, розглядаються як рухомі, а за нерухому прий­мається система, зв'язана з Сонцем (так звана геліоцентрична система).

У машинах і апаратах харчових виробництв, особливо в складних автоматах, у роботах-маніпуляторах досить часто до­водиться одночасно розглядати рух якогось фізичного об'єкта (матеріальної точки) відносно двох і більше систем координат, одна із яких рухається відносно іншої.

Простим і дуже наочним прикладом, що ілюструє необхід­ність двох систем координат, є рух пасажира по палубі рухо­мого корабля, за яким спостерігають з берега. Рух пасажира (точки) відносно спостерігача на березі буде складним, тобто складатиметься з руху корабля і власного руху пасажира від­носно корабля.

Якщо з берегом зв'язати нерухому систему координат, а з кораблем - рухому систему, то рух точки (пасажира) відносно нерухомої системи координат називатимемо абсолютним рухом, а рух відносно рухомої системи - відносним рухом. Рух рухо­мої системи координат відносно нерухомої (корабля відносно берега) називається переносним рухом. Точніше кажучи, пере­носним рухом для даного пасажира буде рух того місця (точки) корабля, у якому пасажир перебуває в даний момент.

Швидкість і прискорення точки у складному русі також відповідно називаються абсолютною, відносною і переносною швидкістю та абсолютним, відносним і переносним прискорен­ням.

Оскільки основними задачами кінематики є визначення за­кону руху і встановлення залежностей між кінематичними характеристиками рухомого об'єкта, то спробуємо записати рівняння складного руху точки.

Нехай точка М рухається по поверхні рухомого тіла (або се­редовища) описуючи деяку криволінійну траєкторію (рис. 2.23). Виберемо нерухому декартову систему координат і рухому систему координат , незмінно зв'язану з тілом (або середовищем).

З точки до точки М прове­демо радіус-вектор , а з точки рухомої системи координат - радіус-вектор . Рух точки О відносно нерухомої точки будемо фіксувати радіусом-вектором . Очевидно, що в кожну мить спра­ведлива рівність

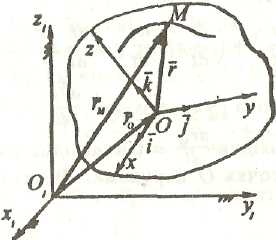
Рис. 2.23.

(2.94)

або

, (2.95)

яка є законом руху точки. Тут - одиничні вектори рухомої системи координат, - проекції радіуса-вектора на рухомі осі.

Абсолютна швидкість точки у складному русі

Для встановлення залежностей між абсолютною, відносною і переносною швидкостями точки в її складному русі розглянемо окремий випадок, коли рухома система (тобто тіло чи се­редовище) лише обертається з кутовою швидкістю і кутовим прискоренням навколо деякої осі ОN, тобто коли переносний рух є обертальним. Тут і надалі для позначення переносного руху застосовуємо індекс е, відносного руху - індекс r, абсо­лютного руху - а.

Швидкість точки М визначимо як першу похідну від радіуса-вектора

, (2.96)

або

. (2.97)

Згідно з визначенням абсолютного руху, похідна є абсолютною швидкістю точки, а похідна внаслідок того, що в нашому окремому випадку точка О нерухома. Векторна сума

(2.98)

є вектором відносної швидкості точки .

Похідні по часу від одиничних векторів являють собою швидкості кінців цих ортів при обертанні тіла навколо осі ОN і можуть бути виражені через кутову швидкість обертання згідно з формулою Ейлера

, (2.99)

де - кутова швидкість переносного обертального руху тіла навколо осі ОN.

Таким чином, третю векторну суму в формулі (2.97) з ура­хуванням виразів (2.99) можемо привести до вигляду

, (2.100)

який визначає переносну швидкість у складному русі точки.

Остаточний вигляд формули (2.97) буде таким

(2.101)

тобто абсолютна швидкість точки в складному русі дорівнює векторній сумі швидкостей відносного і переносного рухів.

Тепер покажемо, що цей висновок справедливий і для випадку поступального переносного руху тіла. Дійсно, при поступаль­ному переносному русі всі точки рухомої системи координат, в тому числі і її початок (точка О), мають однакові швидкості, а напрями одиничних ортів залишаються незмінними і їх похідні по часу дорівнюють нулю.

Таким чином, вираз (2.97) можемо написати у вигляді

. (2.102)

Тут - абсолютна швидкість точки,

- швидкість переносного поступального руху тіла,

- відносна швидкість точки.

Отже формулу (2.102) можемо переписати у такому ж ви­гляді, який ми отримали у випадку переносного обертального руху

, (2.103)

що підтверджує справедливість даної формули як для поступаль­ного, так і для обертального переносного руху тіла.