Випадки визначення положення мцш

При визначенні МЦШ плоскої фігури можуть трапитися кілька випадків, коли положення МЦШ не може бути визначені шляхом побудови перпендикулярів до векторів швидкостей двох точок. Розглянемо ці випадки:

1. Якщо швидкості i двох точок А і В плоскої фігури паралельні між собою, направлені в один бік і перпендикулярні до відрізка АВ (рис. 2.19а), але нерівні (модуль більший за або навпаки), то МЦШ знаходимо на перетині перпендикуляра до швидкостей точок і прямої, що з'єднує кінці векторів i .

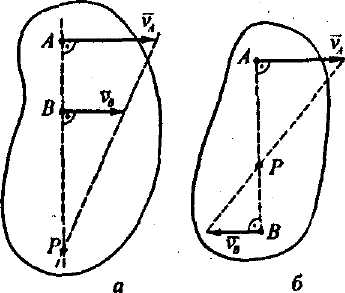
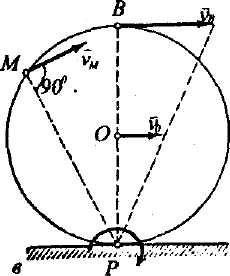
Рис. 2.19.

2. Якщо швидкості двох точок А і В паралельні, перпендикулярні до відрізка _, що їх з'єднує, але направлені в різні боки (рис. 2.19б), то МЦШ знаходимо на перетині АВ з прямою, що з'єднує кінці векторів i .

3. Якщо плоска фігура, наприклад, колесо, рухається так, що його контур котиться без проковзування по деякій нерухомій площині (рис. 2.19в), то точка дотику колеса до площини в даний момент мас нульову швидкість. Отже, точка Р дотику контура плоскої фігури до нерухомої площини є миттєвим центром швид­костей. Швидкості всіх інших точок колеса (напр., точки М) перпендикулярні до прямої, що з'єднує дану точку з точкою Р.

Випадки відсутності мцш

Рухаючись плоско-паралельно, тіло іноді здійснює миттєвий поступальний рух. Тобто в дану мить МЦШ знаходиться на нескінченно великій відстані. У цей момент кутова швидкість плоскої фігури дорівнює нулю і обертання фігури відсутнє. Розглянемо такі випадки:

1. Якщо швидкості i точок А і В паралельні, направлені в один бік, перпендикулярні до відрізка АВ і рівні за модулем (модуль дорівнює модулю ), то провівши пряму, яка з'єднує кінці векторів i , переконаємося, що вона ніколи не перетнеться з прямою АВ (рис. 2.20а).

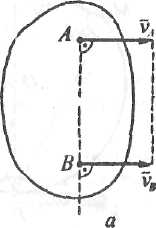
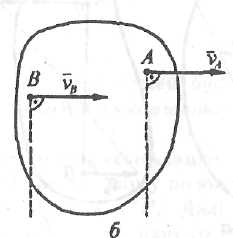
Рис. 2.20.

2. Якщо швидкості i точок А і В паралельні, але пряма АВ не перпендикулярна до векторів швидкостей (рис. 2.20б), то побудувавши в точках А і В перпендикуляри до векторів швидко­стей, переконаємося, що ці перпендикуляри не перетинаються. Отже, тіло здійснює миттєвий поступальний рух, і швидкості всіх його точок рівні ( 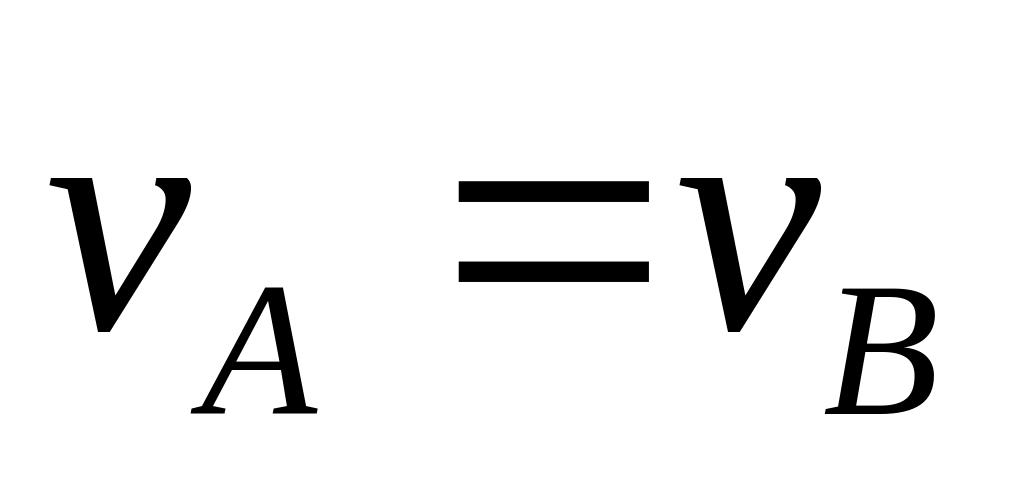), a миттєва кутова швидкість .

Прискорення точок плоскої фігури

Для визначення прискорень точок плоскої фігури існує два способи:

• спосіб полюса;

• спосіб МЦП.

СПОСІБ ПОЛЮСА аналогічний до такого ж способу при визначенні швидкостей точок плоскої фігури і полягає в тому, що прискорення будь-якої точки плоскої фігури дорівнює век­торній сумі прискорення полюса і прискорення даної точки при обертанні плоскої фігури навколо полюса

. (2.83)

Нагадаємо, що за полюс А вибираємо будь-яку точку плоскої фігури, прискорення якої відоме або легко визначається.

Оскільки траєкторією руху точки В при обертанні плоскої фігури навколо полюса А є коло радіуса АВ, то прискорення складається із векторної суми двох взаємно перпендикулярних прискорень - нормального і тангенціального

. (2.84)

Таким чином, при визначенні прискорення будь-якої точки плоскої фігури способом полюса необхідно скласти три вектори: вектор прискорення полюса і вектори нормального і тангенціаль­ного прискорень даної точки при обертанні фігури навколо по­люса:

. (2.85)

Модуль нормального прискорення визначається через мит­тєву кутову швидкість обертання плоскої фігури навколо полюса

, (2.86)

а модуль дотичного прискорення – через миттєве прискорення

. (2.87)

Задачі на визначення прискорень точок плоскої фігури спо­собом полюса розв'язуються або графічною побудовою, або ж проектуванням рівності (2.85) на декартові осі.

СПОСІБ М.Ц.П. Другим способом визначення прискорень точок плоскої фігури є спосіб миттєвого центра прискорень (МЦП). При визначенні швидкостей точок плоскої фігури ми бачили, що в кожну мить існує така точка Р площини, швид­кість якої дорівнює нулю. Аналогічно до цього неважко показати, що існує точка площини - так званий миттєвий центр прискорень, прискорення якої в дану мить дорівнює нулю. При цьому слід наголосити, що миттєвий центр швидкостей і мит­тєвий центр прискорень - це різні точки і співпадають вони лише у випадку, коли тіло мас нерухому точку (але то вже чисто обертальний рух).

Для визначення положення МЦП необхідно мати або прис­корення (модуль і напрям) будь-якої точки плоскої фігури та величини миттєвої кутової швидкості і миттєвого кутового прискорення (застосовується графо-аналітичний метод), або ж мати прискорення двох будь-яких точок плоскої фігури (засто­совується графічний метод).

Г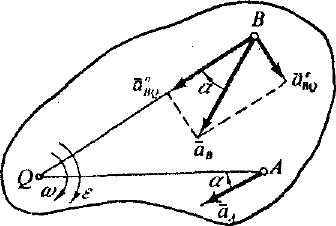 РАФО-АНАЛІТИЧНИЙ МЕТОД визначення положення МЦП. Нехай МЦП плоскої фігури існує (точка Q), і нехай нам відоме прискорення (модуль і напрям) будь-якої точки B (рис. 2.21). Вибираючи точку Q за полюс, маємо записати

Рис. 2.21.

, (2.88)

але оскільки прискорення , то

. (2.89)

Враховуючи вирази (2.86) та (2.87), модуль при­скорення точки В визначимо із формули

, (2.90)

де і - миттєва кутова швидкість і миттєве кутове приско­рення плоскої фігури, QВ - відстань від точки В до МЦП, яка визначається із рівності

.

З розділу про обертання тіла навколо нерухомої осі ми знаємо, що напрям вектора прискорення точки тіла при його обертанні визначається тангенсом кута між вектором прискорення і напрямом нормального прискорення :

.

Таким чином, для визначення положення МЦП графо-аналітичним методом ми робимо лише два кроки. Спочатку век­тор прискорення (рис. 2.21) повертаємо на кут в напрямі обертання фігури (при прискореному обертанні), або в протилежний бік (при сповільненому обертанні). Потім на цьому промені відкладаємо підрізок BQ.

Знайшовши положення МЦП, можемо тепер визначити прискорення будь-якої іншої точки цієї плоскої фігури, наприклад, точки А. Для цього (з'єднаємо точку А з точкою Q і проведемо з точки А вектор під кутом (рис. 2.21). Модуль прискорення точки А визначимо із відношення

. (2.91)

ГРАФІЧНИЙ МЕТОД визначення положення МЦП базується на тій властивості, що вектори прискорень будь-яких точок плоскої фігури утворюють в кожну мить один і той же кут з відрізками, що з'єднують ці точки з МЦП. Переконаємося, що МЦП можна знайти геометрично, якщо відомі напрями і мо­дулі прискорень двох будь-яких точок плоскої фігури, наприклад А і В. Між прискореннями цих двох точок існує зв'язок

, (2.92)

якщо за полюс вибрати точку А (можна і навпаки). З цього рівняння маємо

, (2.93)

де - прискорення точки В при обертанні плоскої фігури навколо полюса А.

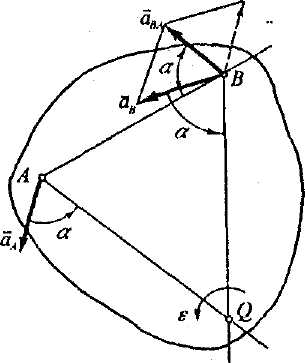
Рис. 2.22.

Побудувавши в точці В вектори і (рис. 2.22), знайдемо прискорення . Оскільки напрям відрізка АВ складає з вектором кут , то вимірявши цей кут, ви­користаємо його для визначення МЦП. Для цього із точок А і В проведемо промені під кутом до векторів і , які перетнуться в точці Q. Це і є МЦП плоскої фігури в дану мить її руху.