Прискорення точок тіла, що обертається

Прискорення точки М тіла, що обертається навколо осі, визначимо як похідну по часу від виразу вектора лінійної швид­кості точки :

. (2.65)

Виходячи о того, що а , для прискорення точки одержимо формулу

або , (2.66)

Рис. 2.12.

Отже, прискорення точки М тіла, що обертається навколо осі, складається із двох векторних доданків. Згідно з правилом векторного множення, вектор добутку перпендикулярний площини векторів і (рис. 2.12) і направлений по дотичній до траєкторії точки М, а вектор добутку перпендикулярний до площини векторів і і направлений від точки М до центру кола С (до осі обертання), тому що саме з боку осі поворот від вектора до вектора відбувається проти годинникової стрілки найкоротшим шляхом.

Таким чином, прискорення будь-якої точки тіла при його обертанні навколо нерухомої осі дорівнює векторній сумі нор­мального і тангенціального прискорень:

, (2.67)

причому

. (2.68)

Модуль дотичного прискорення точки визначається че­рез кутове прискорення тіла і радіус R:

, або . (2.69)

Модуль нормального прискорення точки визначається через квадрат кутової швидкості обертання тіла і радіус R:

або . (2.70)

Наведені вище формули показують, що для визначення при­скорення точки тіла, що обертається навколо осі, повністю при­датні формули, одержані нами при натуральному способі визна­чення руху окремої точки. І ці формули ми отримали б набагато простіше, підставивши вираз лінійної швидкості точки (формула Ейлера) у формулу нормального прискорення точки

; (2.71)

та у формулу дотичного прискорення

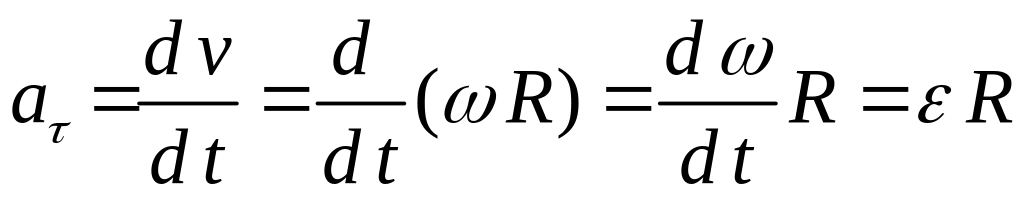. (2.72)

Модуль повного прискорення точки М тіла при обер­танні навколо нерухомої осі знаходиться за теоремою Піфагора і визначається через кутову швидкість і кутове прискорення тіла

або . (2.73)

Напрям вектора повного прискорення визначається аналогічно тому, як це робили у випадку визначення напряму прискорення точки при нату­ральному способі визначення її руху, тобто через тангенс кута між векто­рами повного і нормального прискорень (рис.2.13):

Рис. 2.13.

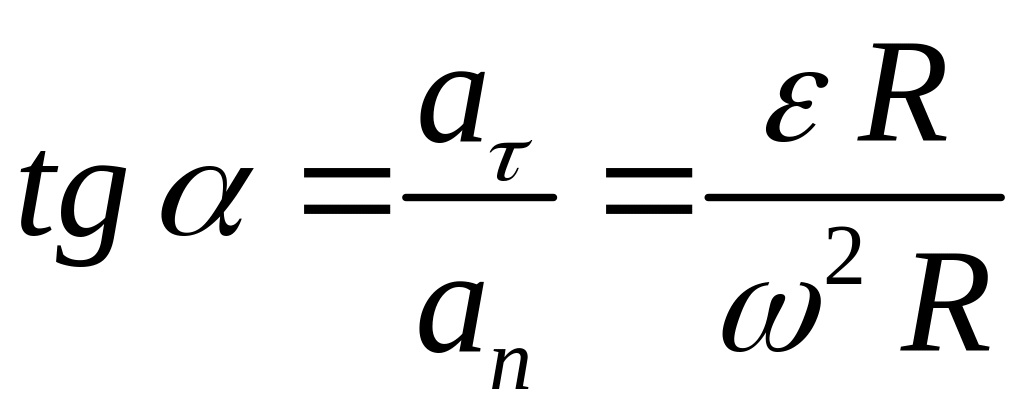або . (2.74)

Плоско-паралельний рух твердого тіла

■

Плоско-паралельним (або плоским) називається такий рух твердого тіла, при якому всі його точки рухаються па­ралельно деякій нерухомій площині. Вивчення цього руху має велике практичне (значення, оскільки плоско-паралельний рух здійснюють багатоланкові механізми більшості машин, які працюють в промисловості, зокрема в харчовій та переробній.

Нехай тверде тіло рухається паралельно деякій неру­хомій площині N (рис. 2.14). Спробуємо дещо спростити задачу вивчення такого руху. Для цього перетнемо тіло площиною Р, паралельною нерухомій площині N. У результаті перетину одер­жимо плоску фігуру S. Виберемо на цій плоскій фігурі деяку довільну точку А. Неважко переконатися, що всі точки тіла, що лежать вище чи нижче точки А, рухаються відносно площини N так само, як і ця точка. Отже немає сенсу вивчати рух всього тіла відносно нерухомої площини N, а достатньо розглянути рух плоскої фігури S у площині Р.

Рис. 2.14.

Виберемо в цій площині осі Оху і визначимо закон руху плос­кої фігури S у цих осях (рис. 2.15). Якби плоска фігура рухалась тільки поступально, то для визначення її руху достатньо було б визначити рух однієї точки (полюса), наприклад, точки А, тобто потрібно було б запи­сати математично закон зміни коорди­нат х і у точки А з часом : .

Рис. 2.15.

Однак плоска фігура може ще й обертатись у своїй площині. Для ви­значення обертального руху необхідно мати закон зміни кута повороту з часом. Цей кут домови­мось вимірювати між віссю абсцис Ох і довільною прямою АВ: .

Таким чином, плоско-паралельний рух тіла звівся до розгляду суми двох простіших рухів: поступального руху плоскої фігури разом о полюсом А і обертального руху навколо полюса. Полю­сом може бути будь-яка точка плоскої фігури, рух якої відомий або легко може бути визначеним. Характеристики обертального руху фігури (кут повороту, кутова швидкість, кутове приско­рення) не залежать від вибору полюса.

Рівняння, що визначають зміну координат полюса і кута повороту з часом

(2.75)

є законом плоско-паралельного руху твердого тіла.