Зв’язок між координатним і натуральним способами визначення руху точки

Якщо рух точки заданий координатним способом (задані координати х,у,z як функції часу), а потрібно визначити пройдену точкою відстань, радіус кривизни траєкторії або дотичне чи нормальне прискорення точки, то потрібно мати формули переходу від однієї системи до іншої.

При координатному способі модуль швидкості точки визначається з формули

, (2.30)

а при натуральному способі - з формули

.

Отже, можемо записати:

,

звідки знайдемо переміщення точки за деякий проміжок часу

.

Модуль дотичного прискорення дорівнює похідній по часу від модуля швидкості, а тому диференціюючи (2.30), одержимо:

, (2.31)

або

. (2.32)

Ця формула є основною формулою зв'язку між координатним і натуральним способами визначення руху точки.

Модуль нормального прискорення можемо виразити так:

або . (2.33)

Тут

. (2.34)

Для визначення радіуса кривизни траєкторії матимемо формулу

. (2.35)

З наведених формул ми бачимо, що вираз (2.32) є основною фор­мулою переходу від координатного до натурального способу.

Осі натурального тригранника

При натуральному способі визначення руху вектор повного прискорення точки мас дві складові - дотичну і нормальну. Одиничний вектор дотичної i перпендикулярний до нього одиничний вектор головної нормалі рухаються разом з точкою по траєкторії і є ортами рухомої системи координат, утворюючи так звану стичну площину. У цій площині лежить відрізок криволiнiйної траєкторії точки.

Побудуємо перпендикулярний до стичної площини одиничний вектор , який називається бінормаллю і дорівнює векторному добутку одиничних векторів (ортів) i :

.

Бiнормаль с ортом третьої осі рухомої правої прямокутної системи координат , яку на­зивають натуральним тригранни­ком.

Грань, що утворюється нормаллю i бінормаллю , називається нор­мальною площиною, а грань, що утворена дотичною та бінор­маллю - спрямляючою площиною (рис. 2.7).

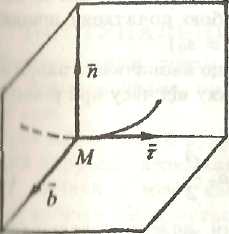
Рис. 2.7.

Вектор повного приско­рення точки лежить у стичній площині, а тому його проек­ція на бінормаль дорівнює нулю: .

Рiвнозмінний та рівномірний рух точки

Якщо модуль швидкості точки, що рухається по довільній траєкторії, змінюється рівномірно з часом, то ми говоримо про рiвнозмінний рух

. (2.36)

Перепишемо рівність (2.36) у вигляді

і проiнтегруємо цей вираз:

. (2.37)

Далі, представивши і записавши рівність (2.37) у вигляді

, (2.38)

ще раз проiнтегруємо і одержимо

. (2.39)

Тут і - сталі інтегрування, які визначаються із почат­кових умов руху точки і являють собою початкову швидкість ( ) і початкову координату ( ).

Таким чином, ми маємо формули, що визначають залежність швидкості точки і пройденого нею шляху від часу при рівнозмінному русі:

. (2.40)

Слід пам'ятати, що цими формулами можна користуватися лише у випадку рівнозмінного руху точки.

Якщо точка рухається рівномірно, тобто , і const, то значення дугової координати (шляху, пройденого точкою по траєкторії) визначається iз формули

, (2.41)

тобто пройдений точкою шлях пропорційний швидкості руху.