Координатний спосіб визначення руху точки

Нехай точка О (рис. 2.3) є початком нерухомої системи координат з одиничними сталими ортами . Тоді радіус-вектор точки М можемо виразити через його проекції :

Рис. 2.3.

. (2.6)

Положення точки в кожен момент часу буде визначеним, якщо будуть відомі координати точки

. (2.7)

Функції (2.7) називаються рівняннями руху або законом руху точки в координатній формі.

Швидкість точки при координатному способі визначимо через компоненти радіуса-вектора точки

, (2.8)

або

, (2.9)

Похідні являють собою проекції вектора швидкості на координатні осі.

Рівність (2 .9) можемо переписати таким чином

, (2.10)

а модуль швидкості визначити з формули

. (2.11)

Напрям вектора швидкості визначається за напрямними косинусами:

. (2.12)

Прискорення точки знаходимо аналогічно формулам (2.8)-(2.10):

,

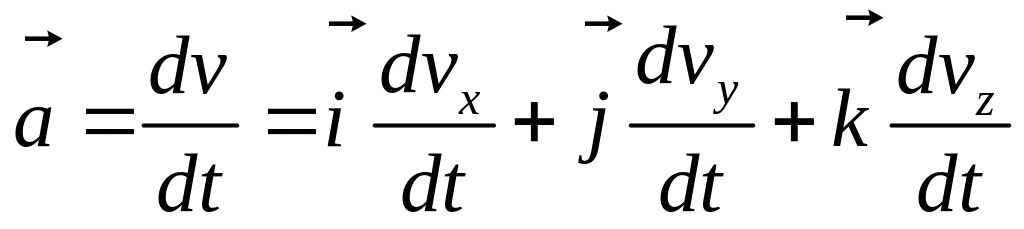або

, (2.13)

Тут

проекції вектора прискорення а на координатні осі.

Модуль прискорення знаходимо, як і модуль швидкості, з формули

. (2.14)

Напрям вектора прискорення також визначається за напрямними і косинусами:

. (2.15)

Крім декартової системи координат, для визначення руху точки по колу в площині Оху застосовуються полярні коорди­нати, а для визначення руху в тривимірному просторі - цилін­дричні та сферичні координати.

У полярних координатах потрібно визначити полярний радіус і полярний кут як функції часу

. (2.16)

У циліндричних координатах до цих двох параметрів додається третя координата по осі Оz. Законом руху будуть такі рівняння

. (2.17)

Перехід від декартових осей до полярних і циліндричних нескладний;

. (2.18)

При визначенні закону руху в сферичних координатах записуються як функції часу полярний радіус і два кути:

. (2.19)

Натуральний спосіб визначення руху точки

Натуральний спосіб розробив і широко використовував у своїх дослідженнях Леонард Ейлер (1707-1783). Він відріз­няється не тільки простотою, але й достатньою наочністю, а тому застосовується як при теоретичних дослідженнях криволінійного руху, так і при практичних розрахунках. Обов'язковою умовою для. застосування натурального способу є наперед відома траєкторія. Найчастіше це є коло радіуса R .

Д ля визначення положення точки М на дузі траєкторії потрібно вибрати початок відліку О та додатній і від'ємний напрями відліку дугової координати s (рис.2.4)

Рис. 2.4.

Тоді положення точки на траєкторії можемо визначити змінною з часом дуговою координатою

. (2.20)

Рівняння (2.20) є законом руху точки при натуральному способі визначення руху.

Швидкість руху точки визначається як похідна по часу від радіуса-вектора

або . (2.21)

Формула (2.21) містить ви­значення як модуля, так і напряму швидкості точки. Для визначення напряму вектора швидкості роз­глянемо рис. 2.5, із якого видно, що при прямуванні модулі величин і стають майже рівними, тобто

як границя відношення довжини нескінченно малої хорди до довжини стягнутої нею дуги.

Напрям одиничного вектора збігається а напрямом до­тичної до траєкторії

Рис. 2.5.

.

Отже, вектор є одиничним вектором (ортом), дотичним до траєкторії точки. Повертаючись до виразу (2.21), можемо за­писати

. (2.22)

Таким чином, при натуральному способі визначення руху швидкість точки за модулем дорівнює похідній по часу від ду­гової координати,

,

а за напрямом збігається з дотичною до дуги траєкторії.

Перейдемо до визначення прискорення точки як похідної від швидкості (2.22)

Диференціюючи, маємо:

. (2.23)

Другий доданок у формулі (2.23) за модулем дорівнює другій похідній по часу від дугової координати і збігається з на­прямом вектора швидкості у випадку прискореного руху точки та протилежний йому при сповільненому русі.

Вираз у першому доданку формули (2.23) перетворимо таким чином:

. (2.24)

Оскільки одиничний орт являє собою вектор зі сталим мо­дулем, то його похідна по скалярному аргументу являє собою векторну величину, перпендикулярну до і направлену до цен­тру кривизни траєкторії (тобто направлена по нормалі ). За модулем величина обернена до радіуса кривизни траєкторії :

.

У результаті замість виразу (2.24) для похідної маємо такий вираз:

. (2.25)

Підставляючи (2.25) у формулу (2.23), а також враховуючи, , а , запишемо формулу для визначення прискорення точки:

. (2.26)

Із формули (2.26) видно, що прискорення точки при натуральному способі визначення руху скла­дається із суми двох взаємно перпендикулярних прискорень: прискорення, направленого по дотичній до траєкторії, яке називається дотичним (або тангенціальним) і за модулем дорівнює , та прискорення, , яке називається нормальним приско­ренням і направлене до центру кривизни траєкторії перпендикулярно до дотичного при­скорення (рис. 2.6).

Рис. 2.6.

Дві складові повного прискорення точки мають не лише аб­страктний, але й реальний фізичний вміст: тангенціальне при­скорення характеризує зміну модуля швидкості з часом, а нормальне прискорення характеризує зміну напряму вектора швидкості.

Якщо точка рухається по прямій, то радіус кривизни і нормальне прискорення дорівнює нулю. Тобто маємо за­пам'ятати, що нормальне прискорення виникає лише при кри­волінійному русі (коли вектор швидкості змінює свій напрям), а тангенціальне прискорення виникає лише при нерівномірному русі (коли змінюється модуль швидкості).

Формулу (2.26) часто записують у вигляді векторної суми двох прискорень

. (2.27)

Тут мається на увазі, що .

Отже, маємо пам'ятати, що при натуральному способі визначення руху прискорення точки дорівнює векторній сумі тангенціального і нормального прискорень.

Оскільки вектори тангенціального і нормального прискорень взаємно перпендикулярні, то модуль повного прискорення точки знаходиться за теоремою Піфагора

. (2.28)

Напрям вектора повного прискорення знайдемо черев тангенс кута між вектором повного прискорення і вектором нормального прискорення (рис. 2.6):

. (2.29)

Порівнюючи координатний і натуральний способи визначення руху точки, які найчастіше застосовуються при розв’язуванні задач механіки, доходимо висновку, що натураль­ний спосіб визначення руху точки, розроблений Леонардом Ейлером, менш громіздкий, більш наочний і найбільш повно ілюструє природу руху, а тому його часто називають "природним" способом..