Центр ваги

На кожну частинку твердого тіла діє сила земного тяжіння, пропорційна масі частинки і прискоренню вільного падіння . Всі ці сили направлені радіально до центру Землі, тобто перетинаються у цьому центрі. Але на практиці ми вважаємо, що сили ваги, які діють на частинки твердого тіла, паралельні між собою. Таке припущення не позначається на наших інженер­них розрахунках тому, що відстані між частинками тіл занадто малі в порівнянні з радіусом земної кулі, який становить близько = 6 400 кілометрів.

Сили ваги є розподіленими силами, тобто діють на всі точки об'єму тіла. Оскільки теоретична механіка оперує лише зосере­дженими силами, то розподілені сили ваги замінюємо рівнодійною силою, яка називається вагою тіла, а точка прикладання рівнодійної сил ваги називається центром ваги тіла.

Центр ваги тіла не змінює свого положення при вільному русі тіла у просторі. Ця властивість дозволяє експериментально визначати центр ваги неоднорідних плоских тіл складної кон­фігурації таким чином: достатньо підвісити тіло на нитці в будь якій його точці і побудувати продовження нитки в тілі (провести вертикаль), а потім підвісити тіло в іншій точці і теж побудувати її продовження. Точка перетину побудованих ліній є цен­тром ваги цього тіла. Центр ваги порожнистих тіл і тіл складної просторової форми може лежати поза межами тіла (наприклад, центр ваги обруча, пустотілого циліндра тощо).

Для аналітичного визначення положення центра ваги скори стаємося теоремою Варіньйона, яка стверджує, що момент рівнодійної сили дорівнює сумі моментів складових сил.

Доведемо справедливість цієї теореми на такому прикладі. Нехай на тіло в точках А і В діють дві паралельні сили і , що мають рівнодійну (рис. 1.25)

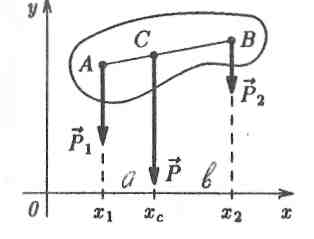
Рис. 1.25.

.

Рівнодійна прикладена в точці С, що ділить відстань між силами обернено пропорційно силам:

, (1.39)

звідки . Момент рівнодійної сили відносно деякої точки О дорівнює

, (1.40)

або

.

Тут - координата точки С. Оскільки із (1.39) маємо , то вираз в останній дужці цього напису дорівнює нулю, і ми одержимо

, (1.41)

що і потрібно було довести згідно з теоремою Варіньйона: момент рівнодійної Р дорівнює сумі моментів складових сил і .

Методом індукції від п до n + 1 неважко покачати, що теорема Варіньйона справедлива для будь-якого числа сил, тобто

. (1.42)

Потрібно зауважити, що теорема Варіньйона справедлива не лише для системи паралельних сил ваги, але й для будь-якої си­стеми сил, яка має рівнодійну.

Із (1.42) знайдемо вираз для аналітичного визначення коор­динати центра ваги тіла по осі Ох:

. (1.43)

Повертаючи тіло на чверть оберта так, щоб сили ваги части­нок тіла були паралельні іншій осі, одержимо аналогічні вирази для визначення двох інших координат центра ваги тіла

. (1.44)

Для визначення положення центра ваги у векторній формі за допомогою радіуса-вектора маємо записати

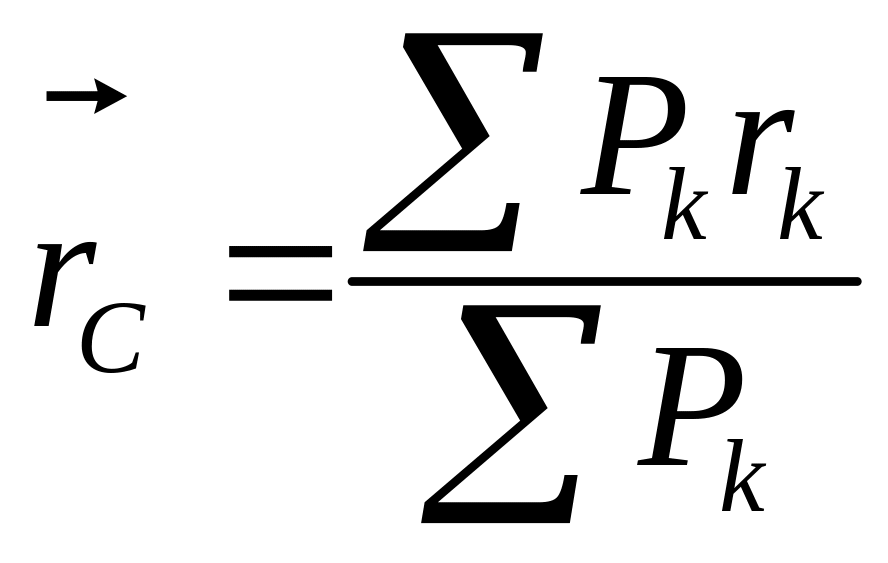. (1.45)

Таким чином, центром ваги тіла називається незмінно зв'язана з цим тілом точка, в якій прикладена рівнодійна сил ваги частинок даного тіла і координати якої визначаються формулами (1.43), (1.44) і.(1.45).

У випадку однорідних тіл вага будь-якої k-ої частинки тіла пропорційна об'єму цієї частинки, а вага всього тіла пропорційна об'єму V тіла:

, a .

Тут - вага одиниці об'єму.

Підставляючи ці значення і у формули для визначення координат центра ваги, ми бачимо, що спільний множник в чисельнику і в знаменнику виноситься за знак суми і скорочується. У результаті одержимо формули для визначення центра ваги тіла як центра ваги об'ємів

. (1.46)

Шляхом аналогічних міркувань легко встановити залежність між вагою однорідної пластинки і її площею S

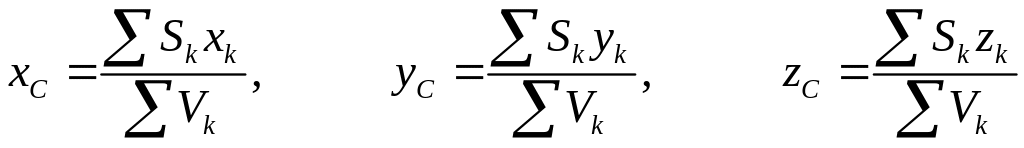, (1.47)

а також між вагою однорідного тонкого стержня (лінії) і його довжиною L :

. (1.48)

Додатково слід вказати деякі способи визначення положення центра ваги, які застосовуються в практиці:

- Спосіб симетрії. Якщо однорідне тіло має площину, вісь чи центр симетрії, то його центр ваги лежить відповідно на площині, на осі чи в центрі симетрії.

- Спосіб розбивання (поділу) на частини. Якщо тіло можна поділити на скінченну кількість таких частин, положення центра ваги яких відоме, то координати центра ваги всього тіла можна безпосередньо визначити із формул (1.43) і (1.44). Якщо ж тіло має отвори (вирізи, порожнини), то в цих формулах вагу (об'єм, площу) отвору віднімаємо.