Федеральное Агентство Железнодорожного транспорта

Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

Петербургский государственный университет путей сообщения

Кафедра «Электрическая тяга»

Якушев А.Я., Викулов И.П., Цаплин А.Е.

Динамические и частотные характеристики структурных звеньев САУ

Методические указания к лабораторной работе

Санкт-Петербург

2013

Цель работы - исследование динамических и частотных характеристик апериодического звена 1-го порядка и колебательного звена 2-го порядка на примерах электрических цепей, содержащих индуктивные катушки и конденсаторы.

1.Виды динамических структурных звеньев

Для математического описания и анализа переходных процессов систему автоматического управления подразделяют на элементарные электрические цепи или устройства, каждое из которых характеризуется дифференциальным уравнением 1-го или 2-го порядка. Передача сигналов в таких цепях осуществляется только в одном направлении от входа к выходу; обратное влияние выходного сигнала на входной отсутствует. Такие устройства или электрические цепи называют звеньями направленного действия или структурными звеньями.

Функциональные элементы системы могут быть представлены комбинацией двух или нескольких структурных звеньев. Схема соединения этих звеньев отображает динамическую структуру функционального элемента. Динамические свойства апериодического звена 1-го порядка в переходном режиме определяются дифференциальным уравнением, характеризующим зависимость изменения во времени выходной переменной и ее производной от изменения входной переменной x(t):

.

Коэффициенты при переменных x и y в уравнении характеризуют рассеяние энергии. Наличие производной в левой части дифференциального уравнения звена связано с элементом, совершающим накопление или отдачу энергии звеном направленного действия. Изменение уровней входной и выходной переменных физических величин структурного звена сопровождается изменением энергетического состояния энергоемких элементов. В электрических цепях это индуктивная катушка или конденсатор, в механических системах это подвижная масса или упругий элемент (пружина).

Каноническая форма дифференциального уравнения апериодического звена 1-го порядка получена в результате деления обеих частей уравнения на коэффициент при выходной переменной:

. (1)

Коэффициент в правой части уравнения является коэффициентом усиления (преобразования) входного сигнала звена, коэффициент при производной выходной переменной имеет размерность времени и называется постоянной времени.

Постоянная времени T характеризует длительность изменения энергетического состояния звена. В физическом смысле постоянная времени звена определяет соотношение между изменением энергии элемента и мощностью потерь, сопровождающих это изменение. В аналитическом представлении постоянная времени звена T определяет промежуток времени, за который выходной сигнал может достигнуть установившегося уровня при ступенчатом изменении входного сигнала, если не будет рассеивания энергии.

Колебательное звено 2-го порядка - это звено, содержащее два различных по физической сущности энергоемких элемента (индуктивную катушку и конденсатор или упругий элемент соединенный механической связью с подвижной массой). В таком звене происходит колебательный обмен энергией, характеризуемый дифференциальным уравнением 2-го порядка:

(2)

Постоянная времени T колебательного звена представляет собой величину, обратную угловой частоте , т.е. период свободных (незатухающих) колебаний выходной переменной:

. (3)

Коэффициент n называют коэффициентом относительного затухания колебаний. Он связывает частоту собственных (затухающих) колебаний ω с частотой свободных колебаний ω₀ следующим соотношением:

.

Период затухающих колебаний определяется выражением:

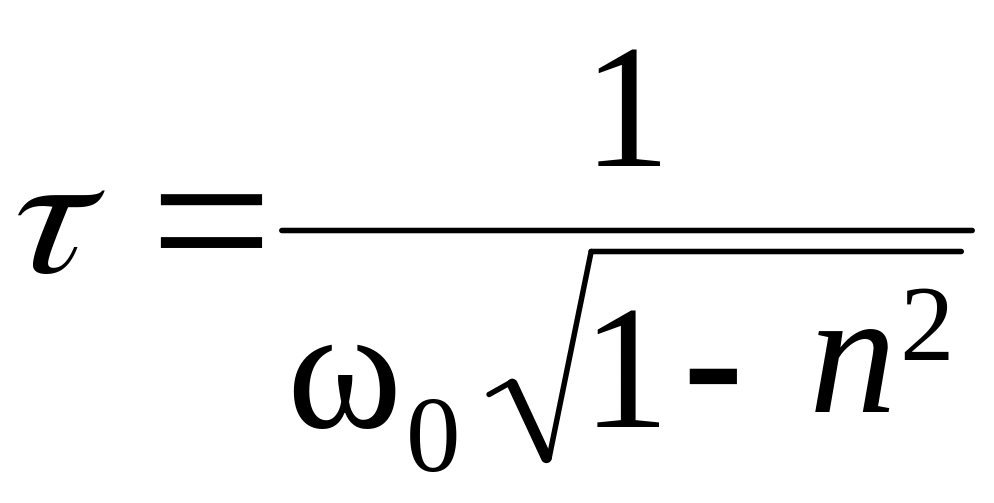. (4)

Если коэффициент затухания , процесс взаимного обмена энергией двух элементов звена разделить нельзя. В этом случае эти элементы представляют собой единое звено второго порядка.

При коэффициенте затухания взаимный обмен энергией между двумя элементами звена становиться невозможным из-за сильного затухания. В этом случае звено второго порядка можно аналитически представить в виде двух апериодических звеньев первого порядка.

2. Динамические характеристики структурных звеньев

Переходной функцией звена направленного действия называют изменение во времени выходного сигнала звена при ступенчатом изменении входной переменной в виде единичной функции 1(t) (рис.1):

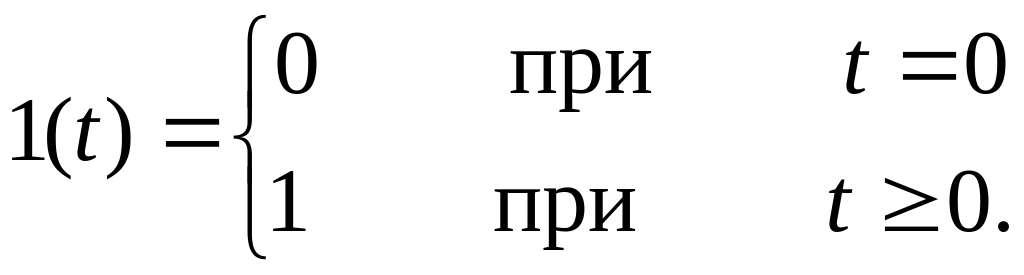
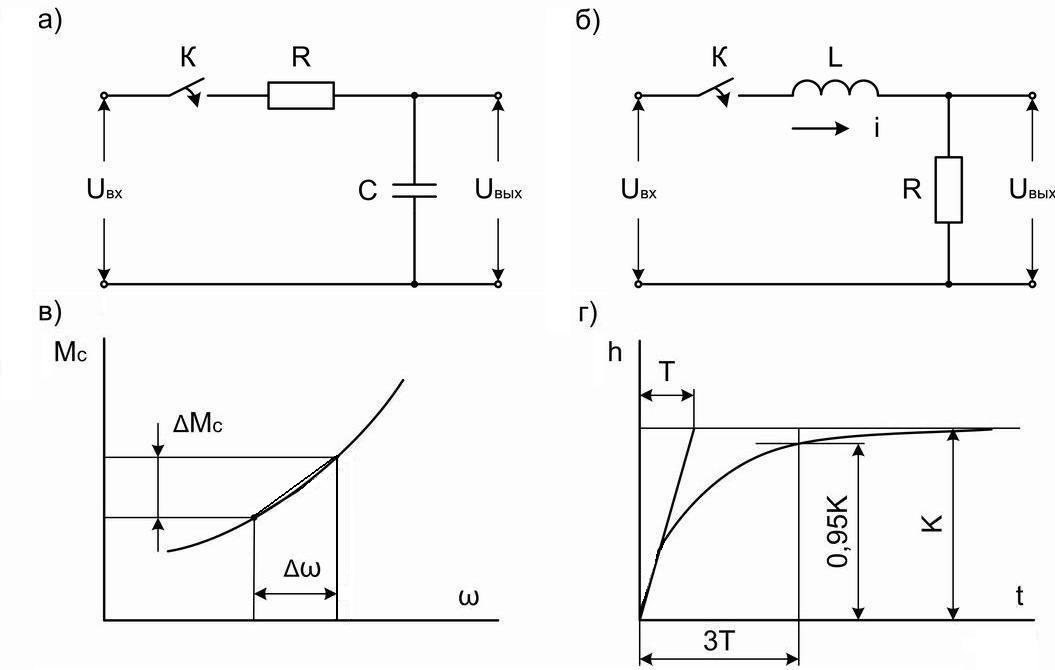
Рис.1

График переходной функции наглядно, с физической точки зрения, показывает, какие изменения претерпевает входной ступенчато изменяющийся сигнал при прохождении через динамическое звено.

Операторным коэффициентом передачи или операторной передаточной функцией называют отношение операторного изображения выходного сигнала к операторному изображению входного сигнала при нулевых начальных условиях:

. (5)

Операторная передаточная функция динамического звена представляет собой аналитическое выражение переходной функции в операторной форме: .

Переходная функция апериодического звена 1-го порядка может быть получена из решения дифференциального уравнения (1) c входной переменной в виде единичной функции :

Переходная функция апериодического звена 1-го порядка в имеет следующий вид:

. (6)

График переходной функции показан на рис.1,б. Он представляет собой экспоненциальную зависимость нарастания выходной переменной при ступенчатом изменении входной. Наибольшая скорость нарастания выходного сигнала имеет место в начале процесса и определяется отношением . Длительность изменения выходной переменной апериодического звена до установившегося уровня считают равной t=3Т. При этом выходная переменная достигает установившегося уровня на 95%.

Операторная передаточная функция апериодического звена 1-го порядка определяется из уравнения (1) звена в операторной форме:

.

В соответствии с выражением (5) она имеет следующий вид:

. (7)

Свойствами апериодического звена 1-го порядка обладают электрические цепи, составленные из конденсатора и резистора или индуктивной катушки и резистора (рис.2,а, б).

Переходные процессы, протекающие в электрической R-C цепи при подаче на вход напряжения в результате замыкания

коммутатора K, характеризуются следующим дифференциальным уравнением:

.

Полученное дифференциальное уравнение соответствует уравнению (1) апериодического звена 1-го порядка. Из сопоставления коэффициентов при переменных в уравнениях следует, что коэффициент усиления цепи K=1, а постоянная времени определяется формулой:

T=RC . (8)

.

Рис.2

Передача сигнала в электрической цепи, составленной из индуктивной катушки и резистора характеризуется дифференциальным уравнением:

или: .

Выходным сигналом такой цепи является падение напряжения на сопротивлении резистора R. Коэффициент усиления цепи с индуктивной катушкой K=1, постоянная времени определяется формулой:

, (9)

Переходная функция колебательного звена второго порядка, полученная из решения дифференциального уравнения (2) звена при входном сигнале в виде единичной функции, имеет вид:

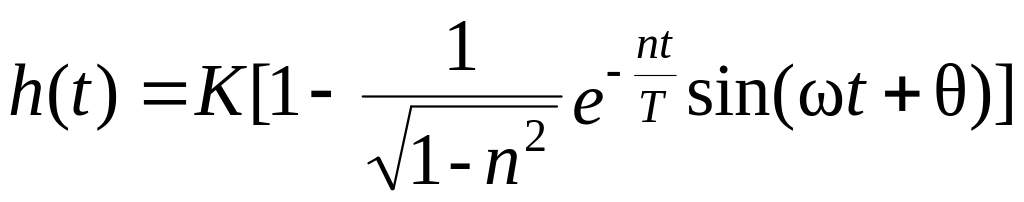. (10)

Здесь - начальная фаза гармонической функции.

Графики переходной функции колебательного звена для коэффициентов относительного затухания: n=0,2; 0,5; 1 показаны на рис.3 .

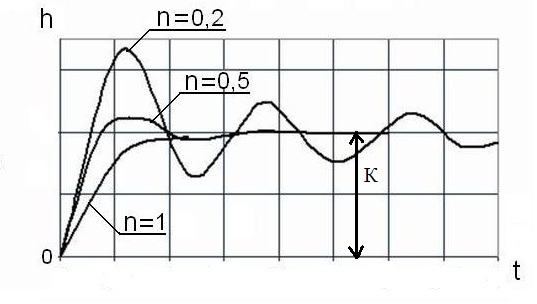
Рис.3

Из рисунка видно, что колебательность переходной функции зависит от коэффициента затухания. При n=0,5 колебательный характер переходной функции близок к апериодическому, а при n=1 переходная функция становится монотонной.

Уравнение колебательного звена 2-го порядка в операторной форме получено из дифференциального уравнения (2) звена:

.

Отсюда операторная передаточная функция колебательного звена 2-го порядка имеет следующий вид:

. (11)

Свойствами колебательного звена 2-го порядка обладает электрическая цепь составленная из конденсатора емкостью С, катушки с индуктивностью L и резистора с сопротивлением R (рис.4).

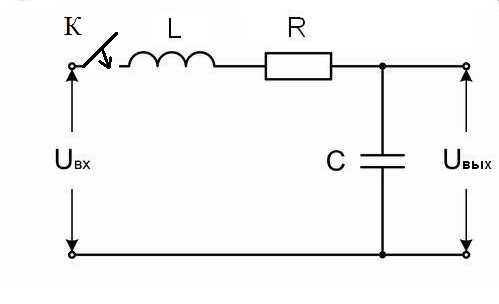
Рис.4. Схема колебательного звена 2-го порядка

Уравнение равновесия напряжений для этой цепи имеетследующий вид:

.

Ток, протекающий по конденсатору, связан с напряжением конденсатора соотношением: . После подстановки этого выражения в уравнение цепи получено уравнение, идентичное каноническому уравнению (2) колебательного звена 2-го порядка.

. (12)

Из сопоставления уравнений (2) и (12) параметры колебательного звена определяется следующими формулами:

постоянная времени - , (13)

частота свободных колебаний - , (14)

коэффициент относительного затухания - , (15)

коэффициент усиления - К=1.