Пример. .

Этот интеграл берется следующим образом:

.

2. Оба показателя степени – целые положительные четные числа (один может быть равен нулю) .

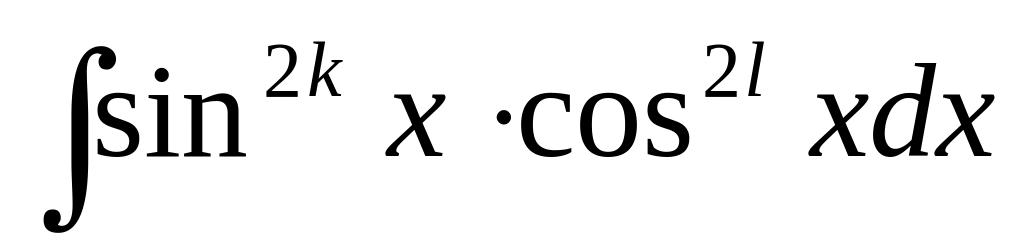Вычислить эти интегралы помогают формулы тригонометрии:

.

Определенный интеграл Задача, приводящая к понятию определенного интеграла

Пусть функция f(x) непрерывна на интервале [a, в] и f(x)  0.

Найти площадь криволинейной трапеции, образованной кривой

y = f(x), осью ОХ и прямыми х = а , х = в.

У

y = f(x)

X

0

a=x₀

_i

₁

x_n=в

x_i+1

x_i

x₁

. . .

. . .

Для решения поставленной задачи разобьем основание криволинейной трапеции - интервал [a, в] произвольным образом на n частей. Обозначим абсциссы точек деления x₀, x₁, x₂ , ... , x_n . Построим в этих точках ординаты.

Обозначим длины полученных частичных интервалов, на которые разбили интервал [a, в], следующим образом:

х₁, х₂, ... , х_n, где х₁ = х₁ - х₀; х₂ = х₂ - х₁ и т.д.

В каждом частичном интервале произвольным образом выберем точки

₁, ₂,... , _n. Вычислим в этих точках значения функции f(₁), f(₂), ... ,f(_n). Заменим каждую i-ю криволинейную трапецию прямоугольником, основание которого есть частный интервал х_i, высота  значение функции в соответствующей точке _i. Площадь элементарной прямоугольной трапеции приближенно равна площади соответствующего прямоугольника.

Найдем площадь ступенчатой фигуры, состоящей из n прямоугольников:

.

Площадь данной криволинейной трапеции приближенно равна площади ступенчатой фигуры. Заставим n возрастать так, чтобы каждый из частичных интервалов х_i уменьшался (наибольший интервал max х_i  0). Предел, к которому стремится площадь ступенчатой фигуры, (если этот предел существует) будет площадью криволинейной трапеции

.

Понятие определенного интеграла

Пусть дана непрерывная функция у = f(x), определенная в интервале [a, в], где а  в. Разделим интервал [a, в] произвольным образом на n частей. Обозначим длины частичных интервалов х₁, х₂, ... , х_n. Такое разбиение интервалов обозначим R. В каждом частичном интервале произвольным образом выберем точки ₁, ₂, ... , _n. Вычислим в них значения функции f(₁) , f(₂) , ... , f(_n) .

Составим сумму парных произведений: . Назовем ее интегральной суммой и обозначим через _R(f): .

Предел, если он существует и не зависит от способа разбиения R и способа выбора точек _i ,к которому стремится интегральная сумма _R(f), когда max x_i  0, называется определенным интегралом от функции f(х) на интервале [a, в] и обозначается следующим образом: ,

где а  нижний предел интегрирования, в - верхний предел интегрирования,

f(х)dx - подынтегральное выражение.

С геометрической точки зрения определенный интеграл равен криволинейной трапеции, ограниченной кривой у = f(х), двумя прямыми х = а, х = в и осью ОХ. При этом считалось, что f(x)  0.

У

Х

в

а

0

у = f(x)

Если f(х)  0 на интервале [а, в], то площадь S такой криволинейной трапеции будет равна .