МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»

Утверждено на заседании кафедры ИСС 28 сентября 2011 г.

Методические указания

по

высшей математике

Часть 2 Неопределенный и определенный интегралы

для бакалавров дневной формы обучения

I курс, 2 семестр

Ростов-на-Дону

2012

УДК 512.8 (08)

Методические указания по высшей математике. Часть 2. Неопределенный и определенный интегралы для бакалавров дневной формы обучения I курс, 2-й семестр:  Ростов н/Д: Рост. гос. строит. ун-т, 2012. 28 c.

Изложен теоретический материал по неопределенным и определенным интегралам.

Предназначены для бакалавров дневной формы обучения специальностей факультета ПГС.

УДК 512.8 (08)

Составители:

канд. физ.-мат. наук, доц. А.Е.Богданов

канд. тех. наук, доц. Г.Я.Корабельников

Рецензент:

д-р физ.-мат. наук, проф. А.А. Ляпин

Редактор Р.Е. Гладких

Темплан 2012 г., поз. 41

Подписано в печать 30.12.2011 Формат 60х84/16

Бумага белая. Ризограф. Уч. - изд. л. 1,2. Тираж 100 экз. Заказ

Редакционно-издательский центр

Ростовского государственного строительного университета

344022, Ростов - на - Дону, ул. Социалистическая, 162

© Ростовский государственный

строительный университет, 2012

Неопределенный интеграл первообразная функция

Определение. Функция F(x) называется первообразной для функции f(x) на интервале (а, в), если F(х) дифференцируема на (а, в) и , для всех

х  (а, в).

Пример. F(x) = Sin2x первообразная для функции f(x) = 2Cos2x для всех х.

Теорема 1. Если F(x) первообразная для f(x) на (а, в), то F(x) + C также первообразная для f(х), где С - произвольная постоянная .

Теорема 2. Если F₁(x) и F₂(x) - две первообразные для функции f(x) на интервале (а, в), то F₁(x) - F₂(x) = С, для всех х  (а, в).

Определение. Множество первообразных для функции f(x) называется неопределенным интегралом от функции f(x) и обозначается .

Если F(x) первообразная для f(x), то . Функция f(x) называется подынтегральной функцией, f(x)dx - подынтегральным выражением, х - переменная интегрирования, С - произвольная постоянная.

Из определения интеграла следует:

1. , т.е. производная от интеграла равна подынтегральной функции. Действие интегрирования проверяется дифференцированием. Продифференцировав результат интегрирования, мы должны получить подынтегральную функцию.

2. .

3. 

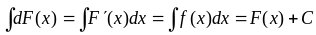
Пример. .

Основная таблица интегралов

1.	2.
	4.
	6.
	8.
9.	10.

Свойства неопределенных интегралов:

Свойство 1. Интеграл от суммы конечного числа функций равен сумме интегралов от слагаемых функций, т.е.

,

где U, V, W - функции от .

Свойство 2. Постоянный множитель подынтегральной функции можно вынести за знак интеграла:

.