Задачи на определение вероятности нахождения вс в пределах вт

1. При использовании БРЛС радиальная СКП определения МВС на масштабе 50 км составляет σ_R = 2 км. Систематическая ошибка m_X = 0.

Определить вероятность нахождения ВС в пределах ВТ при ширина L = 10 км при использовании БРЛС для целей контроля выдерживания ЛЗП.

Формула расчета имеет вид:

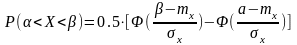. (1)

Подставляя значения получим:

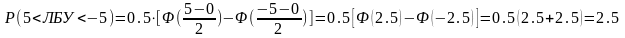
По таблице значений интеграла вероятности находим: Р = 0.9876.

2. При использовании БРЛС радиальная СКП определения МВС на масштабе 125 км составляет σ_R = 5 км. Систематическая ошибка m_X = 0.

Определить вероятность нахождения ВС в пределах ВТ при ширина L = 20 км при использовании БРЛС для целей контроля выдерживания ЛЗП.

Формула расчета имеет вид:

,

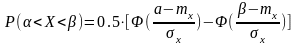Подставляя значения получим:

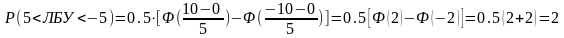
По таблице значений интеграла вероятности находим: Р = 0.9545.

3. Определить значение СКП определения МВС при нахождении ВС с вероятностью 0.95 в пределах трассы шириной L = 10 км.

По таблице значений интеграла вероятности для Р = 0.95 находим значение

Х = 1.96.

Используя формулу (1) получим:

.

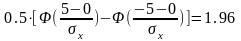Решая это выражение относительно σ_х , получим:

,

.

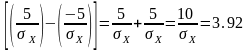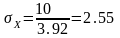км

4. Определить значение СКП определения МВС при нахождении ВС с вероятностью 0.95 в пределах трассы шириной L = 20 км.

По таблице значений интеграла вероятности для Р = 0.95 находим значение

Х = 1.96.

Используя формулу (1) получим:

.

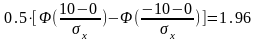Решая это выражение относительно σ_х , получим:

,

.

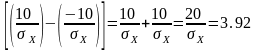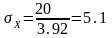км.

Задача на точность наведения

Определить с какой вероятностью ВС будет находиться на участке трассы А369 при использовании VOR/DME KGP и VOR/DME BLH.

Ширина участка трассы А369 – 10 км.

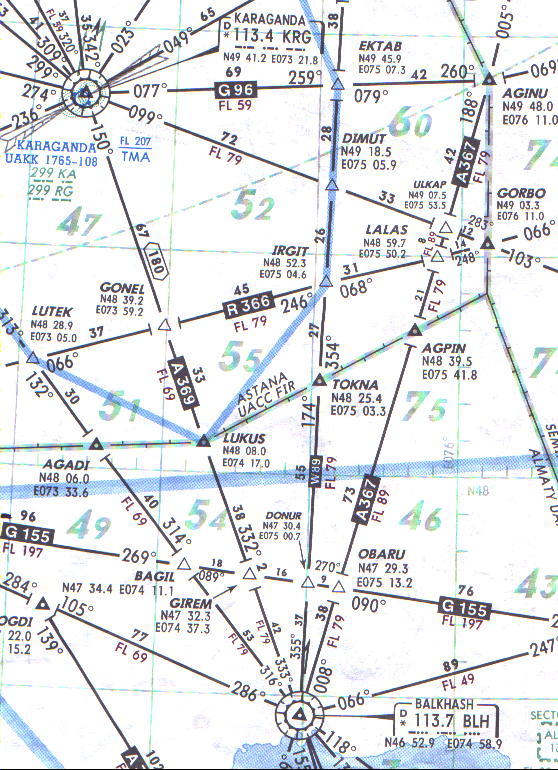1. Наиболее критическая вероятность нахождения ВС будет на середине участка, т.е. на удалении 90 м. миль (166.7 км).

2. При СКП определения радиала по VOR (5.2°)·0.5 линейная погрешность наведения составит:

σ_Л = 0.5·5.2·0.0174·166.7 = 7.54 км.

3. Вероятность нахождения ВС в пределах трассы определиться формулой:

,

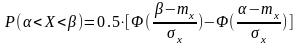где: β – правая граница трассы, равная 5 км;

α – левая граница трассы, равная -5 км;

σ_Х – СКП точности наведения по ЛЗП при использовании VOR;

m_X – математическое ожидание, т.е. систематическая погрешность.

Для VOR систематическая погрешность появляется при изменении магнитного склонения в течение времени. Данная ошибка имеет название Station Declination. При решении задачи примем m_X = 0.

Подставляя значения, получим:

.

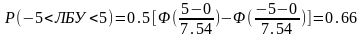По таблице значений интеграла вероятности для х = 0.66 найдем Ф(х) = 0.4937.

Вывод. Вероятность нахождения ВС на середине участка конкретной трассы при контролировании по VOR порядка 0.5, т.е. 50%.

Задача

До какого удаления от VOR при контролировании наведения по VOR вероятность нахождения в пределах трассы будет 95%.

Для вероятности 95% (Ф(х) = 0.95) х = 1.96.

.

.

.

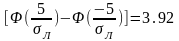Σ_Л = 10 : 3.92 = 2.55 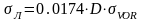км.

.

км.

Вывод.

Контроль пути по направлению с использованием VOR для трассы шириной 10 км на расстояниях более 60 км не гарантирует нахождение ВС в пределах трассы.

Задача на точность определения времени пролета пункта маршрута

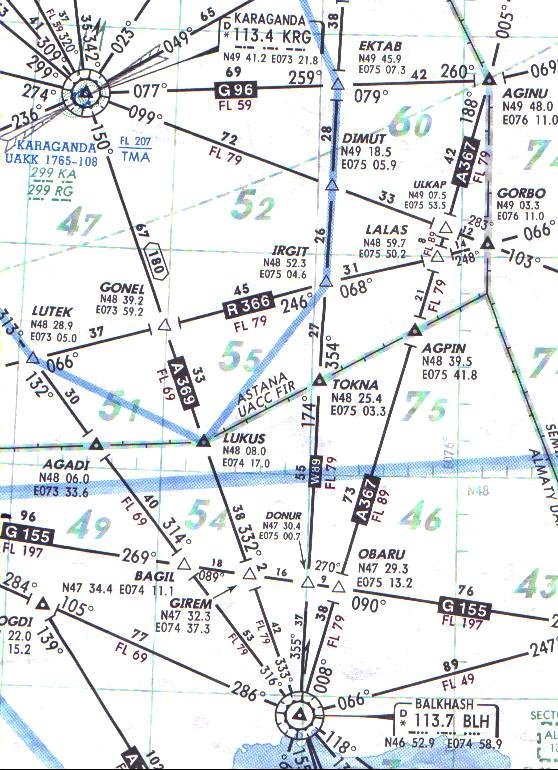
Для определения W скорости можно использовать разность расстояний измеряемых по DME.

Какова вероятность определения пролета пункта Балхаш с точностью 1 мин при сообщении диспетчеру ОВД Балхаш в точке LUKUS?

Изменчивостью ветра на участке LUKUS – BLH пренебречь.

Формулы для расчета:

.

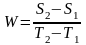Для упрощения формулы (1) длительность измерения W примем: Т₂ – T₁ = t.

(1)

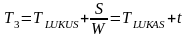, (2)

где: S₁ – первое расстояние от DME KGR;

S₂ – второе расстояние от DME KGR;

Т₁ – время пуска секундомера на расстоянии S₁;

Т₂ – время остановки секундомера на расстоянии S₂;

Т₃ – расчетное время пролета пункта BLH;

T_LUKUS – время пролета пункта LUKUS;

S – расстояние от LUKUS до BLH равное 80 м. миль или 148.2 км.

1. Определение погрешности W.

Продифференцируем формулу (1) по переменным S₁, S₂, t и перейдя от к конечных приращений к СКП получим:

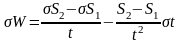. (3)

2. Определить:

σS₁ = 0,46 +0.0125S₁,

σS₂ = 0,46 +0.0125S₂,

σS₂ - σS₁ = (0,46 +0.0125S₂ ) – (0,46 +0.0125S₁) = 0.0125(S₂ - S₁) (4)

Обозначим S₂ - S₁ = Δ.

3. Подставим (4) в (3):

.

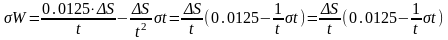Точность отсчета по секундомеру можно принять σt = 1 сек.

При t – 180 сек получим .

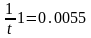С четом длительности определения W 180 с :

.

Для повышения точности определения σW значение t должно быть не менее 3 мин.

Величина 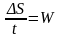. С учетом этого: σW = 0.007W.

При W = 800 км/ч σW = 0.007·800 = 5.6 км/ч.

4. Момент пролета пункта LUKUS определить по DME BLH.

Точность определения момента пролета будет зависеть от погрешности определения расстояния 80 м. миль (148.2 км). Эта погрешность равна:

σS_LUKUS = ±(0,46 +0.0125S_LUКUS ) = ±(0.46 + 0.0125·148.2) = 2.3 км. (5)

5. В связи с тем, что момент пролета пункта LUKUS определяется по расстоянию DME BLH, то из выражения (2) можно записать:

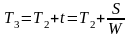. (6)

6. Дифференцируя формулу (6) по переменным S, W и перейдя от конечных приращений к СКП получим:

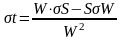. (7)

В формуле (7) примем:

- W = 800 км/ч = 222.2 м/с;

- σS = σS_LUKUS = 2.3 км = 2300 м;

- σW = 5.6 км/ч = 1.5 м/с;

- S = 148.2 км = 148200 м.

Подставив эти значения в (6) получим:

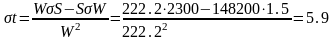с.

Для вероятности 95% 2σt = 2 ·5.9 с = 11.8 ≈ 12 с.

Выводы

При определении W по DME точность расчетного времени пролета пункта маршрута (при условии отсутствия изменения ветра на оставшейся части пути) высокая.