3.2. Основная теорема кинематики

Основная теорема кинематики: При любом движении твердого тела проекции скоростей точек на прямую, соединяющую эти точки, равны.

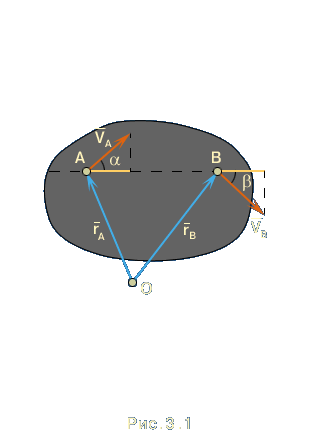
    Для доказательства теоремы используем зависимость радиусов-векторов точек A и B (рис. 3.1 ) .      .     Возведем обе части уравнения в скалярный квадрат. Имеем      , но l = const для твердого тела. Дифференцируя по времени это выражение, получим:      .     Заменив в этом выражении      , получим, имея ввиду, что :      , или .     Раскрывая скалярное произведение векторов, имеем:      , или .

    Очевидно, все точки тела, расположенные на прямой AB , имеют одинаковые проекции скоростей на эту прямую.

    Имеется два простейших вида движения твердого тела, комбинированием которых можно получать другие, более сложные движения. Такими движениями, твердого тела являются поступательное движение и вращение вокруг неподвижной оси.

3.3 Поступательное движение твердого тела

Поступательным движением твердого тела называют такое его движение, при котором любая прямая, жестко скреплена с телом, остается параллельной своему первоначальному положению в каждый момент времени.

    Траектории точек у поступательного движущегося твердого тела могут быть не только прямыми, но и любыми кривыми, в том числе и окружностями.

Теорема о скоростях, ускорениях твердого тела при поступательном движении.     При поступательном движении твердого тела, траектории, скорости и ускорения всех точек тела одинаковы.

    

Выберем две точки A и B твердого тела, радиусы-векторы этих точек удовлетворяют условию (рис. 3.2) :      , где .     Продифференцируем это уравнение      .     В этом соотношении , таким образом      .     Продифференцируем по времени это уравнение, получим      , т.е. .     Поступательное движение твердого тела характеризуется плоскостью движения одной точки. Для задания этого движения достаточно знать координаты какой-либо точки тела, как функцию времени:

, , .

(3.1)

    Эти уравнения являются уравнениями поступательного движения твердого тела.

    Замечание. Понятия скорости и ускорения тела имеют смысл только при поступательном движении. Во всех других случаях речь идет об одной избранной точке тела, например, центре тяжести.

3.4 Вращательное движение твердого тела вокруг неподвижной оси

3.4.1 Угол поворота, угловая скорость, угловое ускорение

Вращением твердого тела вокруг неподвижной оси называется такое его движение, при котором две точки тела остаются неподвижными в течении всего времени движения.

    При этом также неподвижны остаются все точки тела, расположенные на прямой, проходящей через его неподвижные точки. Эта прямая называется осью вращения.

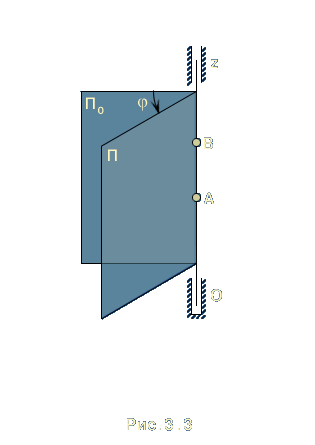
    Через ось вращения проведем неподвижную плоскость и подвижную , скрепленную с вращающимся телом (рис. 3.3) . Тогда в момент времени t положение подвижной плоскости и, следовательно твердого тела определяется углом между плоскостями - . Угол называется углом поворота тела.

    Положение тела относительно выбранной системы отсчета полностью определяется в любой момент времени, если задано уравнение

,

(3.2)

где – любая дважды дифференцируемая функция. Это уравнение называют уравнением вращения твердого тела вокруг неподвижной оси.     Угол считается положительным, если он откладывается против часовой стрелки, если смотреть с положительного направления оси Oz . Траектории точек тела при его вращении вокруг неподвижной оси являются окружностями, расположенными в плоскостях, перпендикулярных оси вращения.

    Введем понятие алгебраической угловой скорости и углового ускорения.

Алгебраической угловой скоростью тела в какой-либо момент времени называют первую производную по времени от угла в этот момент, т.е. .

Она является величиной положительной при вращении тела против часовой стрелки, так как угол поворота возрастает с течением времени, и отрицательной – при вращении тела по часовой стрелке, потому что угол поворота при этом убывает.     Модуль угловой скорости обозначают . Тогда

(3.3)

    Размерность угловой скорости [ ] = угол/время = рад/с = с^-1. В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За 1 мин. тело повернется на угол , если – число оборотов в минуту. Разделим этот угол на число секунд в минуту, получим      .

Алгебраическим угловым ускорением тела называют первую производную по времени от алгебраической угловой скорости, т.е. вторую производную от угла поворота .

    Модуль углового ускорения обозначим , тогда

(3.4)

    Размерность углового ускорения [ ] = рад/с² = с^-2.     Если , - тело вращается ускоренно в положительную сторону (против часовой стрелки). При , тело вращается ускоренно в отрицательную сторону. При , - замедленное вращение совершается в отрицательную сторону.     Угловую скорость и угловое ускорение на рисунках изображают дуговыми стрелками вокруг оси вращения тела.