1.9 Ускорение точки
Движущая
точка M
в момент времени
имеет
скорость
(рис. 1.7)
. В момент времени
эта
точка занимает положение
,
имея скорость
.
Чтобы изобразить приращение скорости
за
время
,
перенесем вектор скорости параллельно
самому себе в точку M.
Средним
ускорением
точки
за
время
называется
отношение
,
т.е.
|
(1.3) |
Ускорением точки в момент времени называют предел, к которому стремиться среднее ускорение при , стремящемуся к нулю, т.е.
|
(1.4) |
Приращение скорости , и, следовательно, направлено внутрь вогнутости траектории.
Скорость - это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета. |
Ускорение - это векторная величина, которая характеризует быстроту изменения модуля и направления скорости точки. |
2.1 Векторный способ задания движения точки
2.2 Координатный способ задания движения точки
2.3 Естественный способ задания движения точки
2.3.1 Определения
2.3.2 Оси естественного трехгранника
2.3.3 Дифференцирование единичного вектора
2.3.4 Скорость и ускорение при естественном способе задания движения
2.4 Движение точки в полярных координатах
2.1 Векторный способ задания движения точки
Движение
точки относительно рассматриваемой
системы отсчета при векторном способе
изучения движения задается радиусом-вектором
этой
точки. Движение точки считается заданным,
если известен радиус-вектор движущейся
точки как функция времени, т.е.
Задание векторного уравнения движения полностью определяет движение точки. |
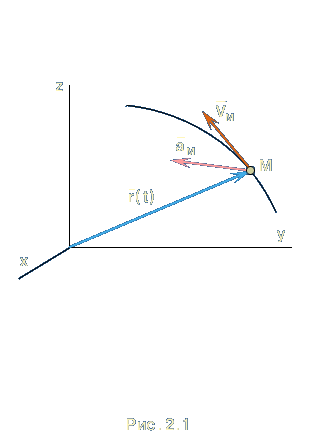
Траекторией точки является годограф радиуса-вектора. Скорость точки направлена по касательной к траектории (рис. 2.1 ) и вычисляется, согласно (1.2), по формуле
|
(2.1) |
для ускорения точки имеем:
|
(2.2) |
Пример 1. Движение точки задано уравнением
Решение. Построить траекторию движения точки, значит построить годограф радиус-вектора. Для изображения годографа составим таблицу точек годографа для отдельных значений t: Таблица
Для
любой точки годографа имеем:
Точка
Для
нахождения скорости, найдем производную
радиус-вектора:
|
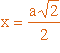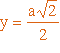Построить
траекторию движения точки и определить
ее скорость при
.
,
,
,
поэтому при любом t
выполняется равенство
,
т.е. все точки годографа лежат на
цилиндре, направляющей которого
является окружность
в
плоскости переменных x,
y,
а образующая параллельна оси z.
Искомый годограф имеет вид, изображенный
на (рис. 2.2
а)
, и он называется винтовой линией.
при
имеет
координаты:
,
,
.
При
(рис. 2.2
б)
Скорость
лежит на касательной к точке. Уравнение
касательной к винтовой линии имеет
вид
