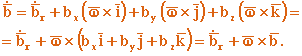5.2. Сложение скоростей

    Определим скорость абсолютного движения точки, если известны скорости относительного и переносного движений этой точки.

Теорема. Абсолютная скорость материальной точки равна геометрической сумме ее переносной и относительной скоростей    (5.1)

    Рассмотрим два близких положения подвижной системы в момент времени и .

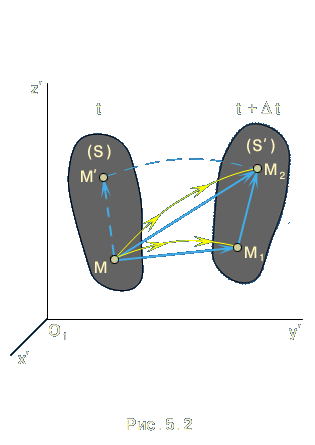
    В момент времени точка занимает положение M . В момент времени вследствие относительного движения точка окажется в положении , а за счет переносного движения за это время точка переместится в положение (рис. 5.2) . Перемещение точки в абсолютном, относительном и переносном движениях представляются соответственно векторами , , . Вектор равен геометрической сумме векторов и :      .     Средняя абсолютная скорость точки M за время , по определению, равна отношению вектора перемещения ко времени , т.е.      .     Вектор определяет среднюю относительную скорость точки в подвижной системе координат S , вектор представляет среднюю скорость переносного движения, поэтому равенство можно переписать в виде

     .

    В пределе при векторы , и дают значения мгновенных скоростей в абсолютном, переносном и относительном движениях, т.е.      .     Полученная теорема имеет важное значение в механике.

5.3. Абсолютная и относительная производная от вектора. Формула Бура

    Установим зависимость между полной и относительной производными по времени вектора и величинами, характеризующими движение подвижной системы отсчета относительно неподвижной (рис. 5.3) . Для этого разложим вектор на составляющие, параллельные осям подвижной системы координат.

Имеем

(5.2)

    Изменение вектора относительно неподвижной системы координат , , , в зависимости от времени состоит из изменения его проекций , , на подвижные оси координат и изменения единичных векторов , , подвижных осей, вследствие движения подвижной системы координат относительно неподвижной. Вычислим полную производную по времени от вектора , используя формулу (5.2). Получим:      .     Первые три слагаемых учитывают изменение вектора при неизменных , , и поэтому составляют относительную производную, которую обозначают .      .     Производные по времени единичных векторов определим по формулам Эйлера (лекция 3, формула 3.11)      , тогда, полная производная

(5.3)

    Полученная формула называется формулой Бура.

5.4. Сложение скоростей точки в общем случае переносного движения

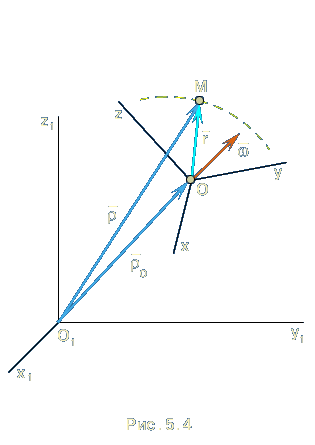
    Движение подвижной системы координат относительно неподвижной можно охарактеризовать скоростью ее поступательного движения , например вместе с точкой O и вектором угловой скорости ее вращения вокруг O . Пусть точка M движется относительно подвижной системы координат. Получим теорему сложения скоростей. Проведем векторы , характеризующие положение точки M относительно неподвижной и подвижной систем осей координат, и вектор точки O (рис. 5.4) .

Тогда, для любого момента времени      .     Продифференцируем по времени это векторное тождество      .     По определению - является абсолютной скоростью точки M , - абсолютная скорость точки O . Для величины применим формулу Бура (5.3). Имеем 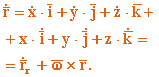     .     Относительная производная является относительной скоростью точки M по отношению к подвижной системе отсчета, - угловая скорость вращения подвижной системы отсчета и, следовательно, радиуса-вектора , если бы он в рассматриваемый момент времени был скреплен с подвижной системой осей координат. Таким образом, получаем

(5.4)

    Сравнивая полученное выражение с (5.1), получаем, что скорость является скоростью точки свободного твердого тела, скрепленного с подвижной системой координат, с которой в данный момент совпадает точка M в движении тела относительно неподвижной системы осей координат. Это и есть переносная скорость точки M , тогда:

(5.5)

т.е. скорость абсолютного движения точки равна векторной сумме переносной и относительной скоростей.

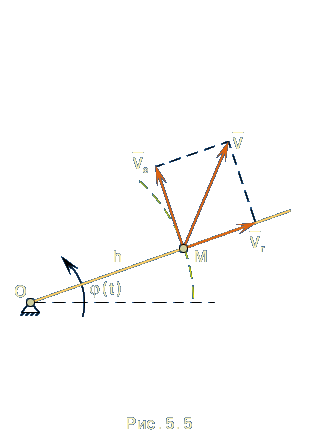
Пример. Стержень вращается в плоскости вокруг своего неподвижного конца О с угловой скоростью . Точка M скользит вдоль стержня со скоростью V . Определить абсолютную скорость точки (рис. 5.5) .      Решение     Точка участвует в двух движениях. Она перемещается вместе со стержнем, и, кроме того, движется вдоль стержня. Относительно стержня точка совершает прямолинейное движение со скоростью V , поэтому, приняв за подвижную систему стержень, значение относительной скорости совпадает со скоростью , .     Для определения переносной скорости точки рассмотрим движение той точки стержня, которая в данный момент совпадает с движущейся точкой M . В переносном движении точка описывает окружность вокруг точки O со скоростью , поэтому переносная скорость точки будет равна      .     Так как векторы и ортогональны, имеем      .