 Автор лекций И.В.Богомаз

 Компьютерная графика, программирование и дизайн С.В.Кухтецкий Л.П.Михайленко

 Красноярская государственная  архитектурно-строительная  академия, 1999

г. Красноярск, КрГАСА

2005

Лекция 1. Основные понятия, задачи кинематики

    1.1. Пространство и время

     1.2. Материальная точка, механическая система, абсолютно твердое тело

    1.3. Задачи кинематики

    1.4. Важнейшие системы координат

    1.5. Векторы

    1.6. Радиус – вектор

    1.7. Траектория точки

    1.8. Скорость точки

    1.9. Ускорение точки

Лекция 2. Способы задания движения точки

    2.1. Векторный способ задания движения точки

    2.2. Координатный способ задания движения точки

    2.3. Естественный способ задания движения точки

        2.3.2. Оси естественного трехгранника

        2.3.3. Дифференцирование единичного вектора

        2.3.4. Скорость и ускорение при естественном способе задания движения

    2.4. Движение точки в полярных координатах

Лекция 3. Простейшие движения твердого тела

    3.1. Понятие о степенях свободы

    3.2. Основная теорема кинематики

    3.3. Поступательное движение твердого тела

    3.4. Вращательное движение твердого тела вокруг неподвижной оси

        3.4.1. Угол поворота, угловая скорость, угловое ускорение

        3.4.2. Частные случаи вращения твердого тела

        3.4.3. Скорости и ускорения точек твердого тела

    3.5. Преобразование простейших движений

    3.6. Векторы угловой скорости и углового ускорения

Лекция 4. Плоское движение твердого тела

    4.1. Уравнения плоско-параллельного движения твердого тела

    4.2. Скорости точек твердого тела при плоскопараллельном движении

    4.3. Мгновенный центр скоростей (МСЦ)

        4.3.1. Теорема о скоростях

        4.3.2. Частные случаи

    4.4. Ускорение при плоскопараллельном движении твердого тела

    4.5. Основные способы вычисления углового ускорения при плоском движении

Лекция 5. Сложное движение точки

    5.1. Основные понятия

    5.2. Сложение скоростей

    5.3. Абсолютная и относительная производная от вектора. Формула Бура

    5.4. Сложение скоростей точки в общем случае переносного движения

    5.5. Сложение ускорений точки в общем случае переносного движения

    5.6. Ускорение Кориолиса

1.1 Пространство и время

1.2 Материальная точка, механическая система, абсолютно твердое тело

1.3 Задачи кинематики

1.4 Важнейшие системы координат

1.5 Векторы

1.6 Радиус – вектор

1.7 Траектория точки

1.8 Скорость точки

1.9 Ускорение точки

Теоретическая механика изучает механические явления на основе законов природы (аксиом). Кинематика, раздел теоретической механики, изучает движение материальных тел не интересуясь причинами, вызывающих или изменяющих это движение. Для нее важны лишь физическая обоснованность и математическая строгость в рамках принятых моделей.

1.1 Пространство и время

    Механическое движение происходит в пространстве и времени. В теоретической механике в качестве моделей пространства и времени принимаются их простейшие модели – абсолютное пространство и абсолютное время, существование которых постулируется. Абсолютное пространство и время считаются независимыми одно от другого, в этом состоит основное отличие классической модели пространства и времени от их моделей в теории относительности, где пространство и время взаимосвязаны.

    Предполагается, что

абсолютное пространство представляет собой трехмерное, однородное и изотропное неподвижное евклидово пространство.

    Для небольших по размерам областей реального физического пространства евклидова геометрия справедлива.

Абсолютное время в теоретической механике считается непрерывно изменяющейся величиной, оно течет от прошлого к будущему. Время однородно, одинаково во всех точках пространства и не зависит от движения материи.

    Движение в его геометрическом представлении имеет относительный характер – одно тело движется относительно другого, если расстояния между всеми или некоторыми точками этих тел изменяются. Для удобства выбирается определенное твердое тело, которое считается неподвижным. Тогда , любое другое движение по отношению к этому телу будем считать абсолютным движением. В качестве неподвижного тела отсчета выбирают систему трех не лежащих в одной плоскости осей (часто взаимно ортогональных), называемую системой отсчета, которая по определению считается неподвижной (абсолютной) системой координат. В кинематике этот выбор произвольный. В динамике такой произвол недопустим.

    В результате почти столетнего обсуждения научная и техническая общественность всех стран мира пришла к заключению, что наиболее целесообразной является Международная система единиц (СИ). В качестве основных в СИ взяты для кинематики единицы длины (метр) и времени (секунда).

Метр равен расстоянию, проходимому в вакууме плоской волной за 1/299792458 долей секунды.

Секунда равна продолжительности 9,192631770∙109 колебаний излучения, соответствующему квантовому переходу между уровнями F = 4, = 0 и F = 3, = 0 сверхтонкой структуры основного состояния атома .

1.2 Материальная точка, механическая система, абсолютно твердое тело

    Объектами изучения в кинематике являются

• материальная точка;

• механическая система;

• абсолютно твердое тело.

Материальная точка – тело конечной массы, положение и движение которого в пространстве можно определять как для объекта, не имеющего размеров, т.е. геометрической точкой.

    Это условие выполнено, если при изучении движения можно пренебречь размерами частицы и ее вращением. Можно или нельзя принять материальный объект за материальную точку, зависит от конкретной задачи.

Механическая система (или просто система) – выделенная каким -либо образом совокупность материальных точек.

Абсолютно твердое тело (или прости тело) – механическая система, расстояние между точками которой не меняются при взаимодействиях.

    Абсолютно твердое тело является моделью материального тела.

1.3 Задачи кинематики

    Задать движение материальной точки (системы)- это значит дать способ определения положения точки (всех точек, образующих систему) в любой момент времени.     Задачи кинематики состоят в разработке способов задания движения точки (системы) и методов определения скорости, ускорения точки и других кинематических величин точек, составляющих механическую систему.

1.4 Важнейшие системы координат

    Пространство, в котором мы живем, является трехмерным. Это означает, что положение точек в нем характеризуется тремя числами. Положение точек в двумерном пространстве характеризуется двумя числами. Какими именно числами - зависит от системы координат, с помощью которой описывается положение точек пространства и плоскости. Рассмотрим наиболее важные из них.

    На плоскости:

• прямоугольная декартова система координат;

• полярная система координат.

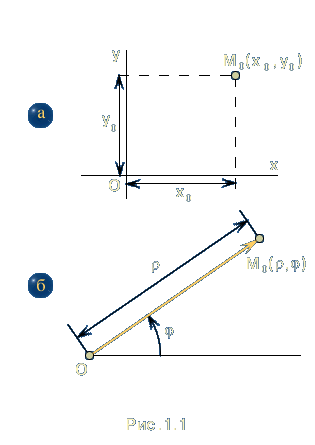
В прямоугольной декартовой системе координат (рис. 1.1 a) двумя числами, характеризующими положение точки , являются длины и .

В полярной системе координат (рис. 1.1 б) двумя числами, характеризующими положение точки , являются длина и угол .

    Следует отметить, что возможны две прямоугольные декартовы системы координат, которые никакими движениями в пространстве не могут быть совмещены друг с другом. Одна из них называется правой, другая - левой. Они различаются взаимной ориентацией осей. На (рис. 1.2 a) изображена правая система. В левой системе оси X и Y меняются местами. Практически в подавляющем большинстве случаев применяется правая система , как стандартная. Необходимо иметь в виду, что при переходе от правой системы к левой изменяются знаки в некоторых формулах.

    В пространстве наиболее важными системами координат являются:

• прямоугольная декартова;

• цилиндрическая;

• сферическая.

В прямоугольной декартовой системе координат тремя числами, характеризующими положение точки, являются длины , и (рис. 1.2 a) .

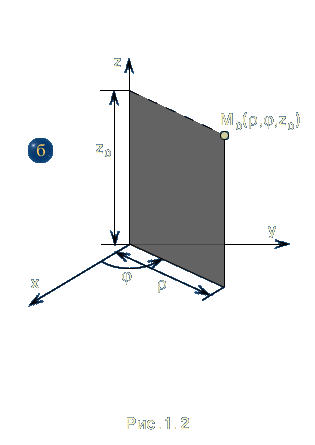
В цилиндрической системе координат тремя числами, характеризующими положение точки , являются длина , угол и длина z (рис. 1.2 б) .

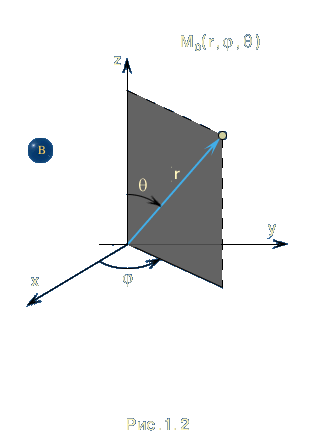
В сферической системе координат тремя числами, характеризующими положение точки , являются длина , углы и (рис. 1.2 в) .

Числа, определяющие положение точки в некоторой системе координат, называются координатами точки.

Формулы, связывающие координаты точки в одной системе с ее координатами в другой, называют преобразованием координат.

    Приведем формулы преобразования между цилиндрическими, сферическими и декартовыми координатами.     Преобразование от цилиндрических к декартовым прямоугольным          Преобразование от сферических к декартовым