§3. Фокусы, фокусные расстояния и фокальные плоскости оптической системы

Практическая полезность формулы (2.3а) для параксиальных лучей состоит, в частности, в том, что она позволяет вычислить положение изображения А’ при известном положении предмета А и, наоборот. При этом важным является случай, когда a = - , т. е. точка А действительного предмета находится достаточно далеко от сферической границы. В этом случае точка, сопряженная с точкой А обозначается F’ и называется задним фокусом оптической системы, отрезок а^' = Н'Р’ обозначается f’ и называется задним фокусным расстоянием оптической системы (рис. 3а). Вертикальная плоскость (нормальная к оптической оси), содержащая точку F', называется задней фокальной плоскостью. Таким образом, точка F’ сопряжена с точкой А бесконечно удаленного действительного предмета, лежащей на оптической оси. Соответственно, задняя фокальная плоскость сопряжена с бесконечно удаленной действительной плоскостью. Из формулы (2.3а) получим, что при a = - 

(3.1)

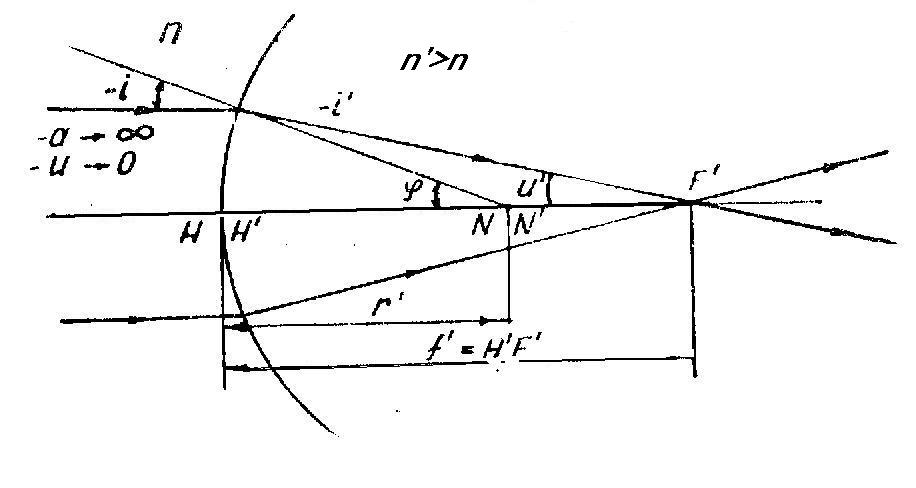В случае одной преломляющей сферической границы с учетом формулы (2.4) имеем: (3.1а)

Рис.3а

Аналогично (рис.36), полагая a‘ = , введем понятия переднего фокуса F, переднего фокусного расстояния f и передней фокальной плоскости:

(3.2)

В случае одной преломляющей сферической поверхности

(3.2а)

Р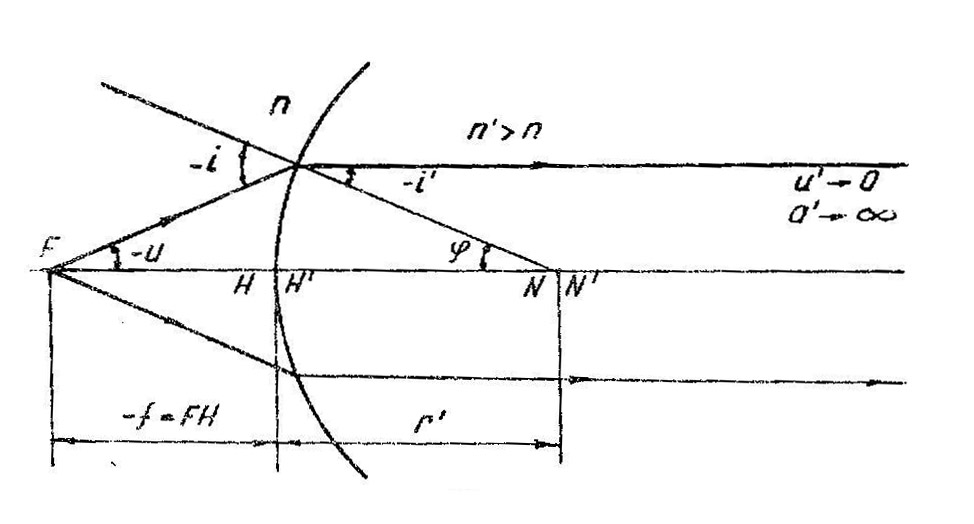 ис.3б

Таким образом, передний фокус F сопряжен с точкой А^’, находящейся на оптической оси в пространстве изображений и бесконечно удаленной от точки Н’. Как следует из (3.1) и (3.2) абсолютные величины фокусных расстояний f и f’, вообще говоря, не равны друг другу:

(3.3)

Лишь в частном случае, когда оптическая система находите в однородной среде (n’=n),  f = f’. Это имеет место, например, для лупы, окуляра микроскопа, телескопа и других оптических систем, находящихся в воздухе. Формулы (3.1 – 3.3) верны для любой оптической системы. Формулы (3.1а) и (3.2а) справедливы только для одной преломляющей сферической границы. Заметим, что в последнем случае если r>о и n’>n ,то f’>r всегда, в то время как f может быть и больше и меньше r. Введение фокусных расстояний f и f’ позволяет несколько иначе записать формулу (2.3). Если разделить все члены формулы (2.3а) на Ф, то с учетом (3.1) и (3.2) получим:

(3.4)

В случае оптической системы, находящейся в однородной среде, f = - f’ и

(3.5)

Для экспериментального определения фокусного расстояния оптической системы (толстой линзы, объектива и т.п.) удобно использовать формулу Ньютона (3.7), в которой положение предмета АВ и его изображения A’B’ (рис. 4) определяются отрезками –x и x’, отсчитываемыми от фокусов F и F’. Из рис.4 имеем:

(3.6) или

x x’ = f f’ (3.7)

При n’ = n (например, линза в воздухе)

x x’ = - f ² = -f’ ² (3.7а)

Рис.4

Рис. 4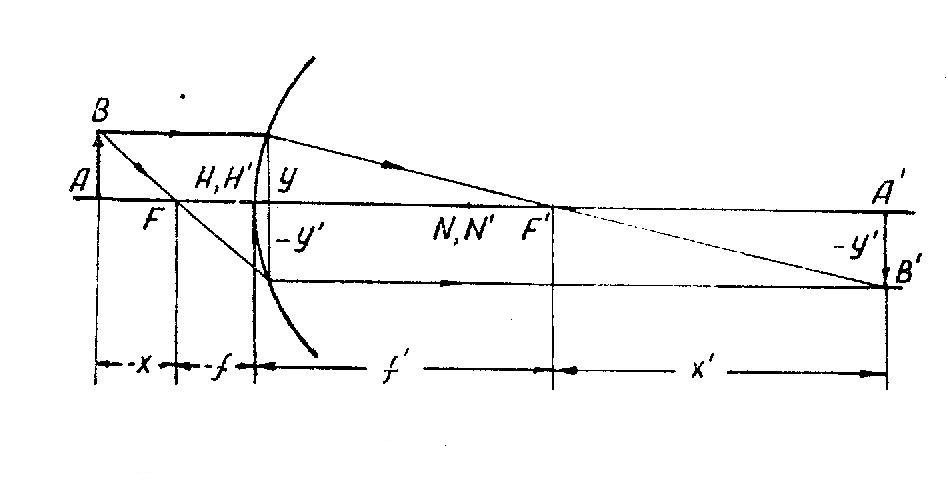

§4. Увеличение оптической системы

Н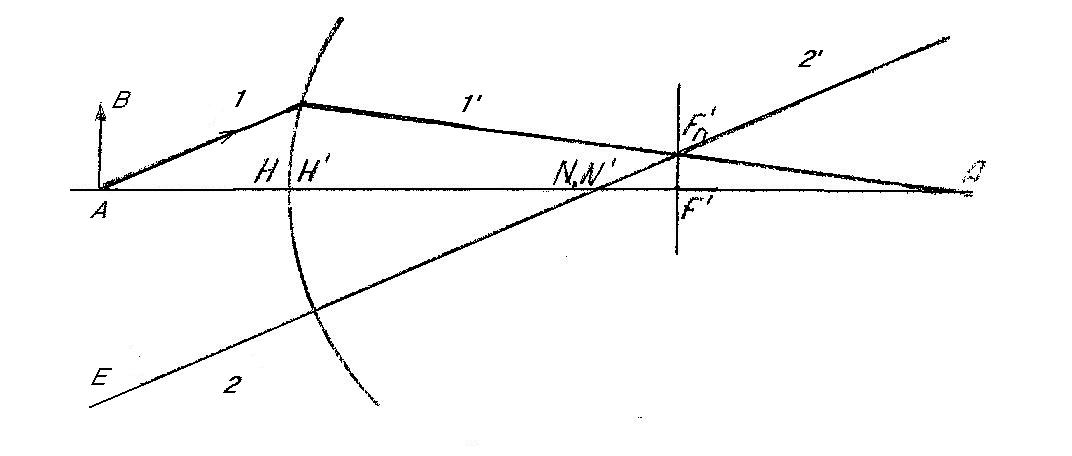 а рис. 5а показан прием построения изображения А’ действительной точки А, находящейся на оптической оси. На рис.5б, показаны 4 приема построения изображения В^’ действительной точки В, не лежащей на оптической оси. На рис. 5в и 5г показаны аналогичные приемы построения

Рис. 5а

Рис. 5б

Рис. 5б

Рис. 5б

Рис. 5в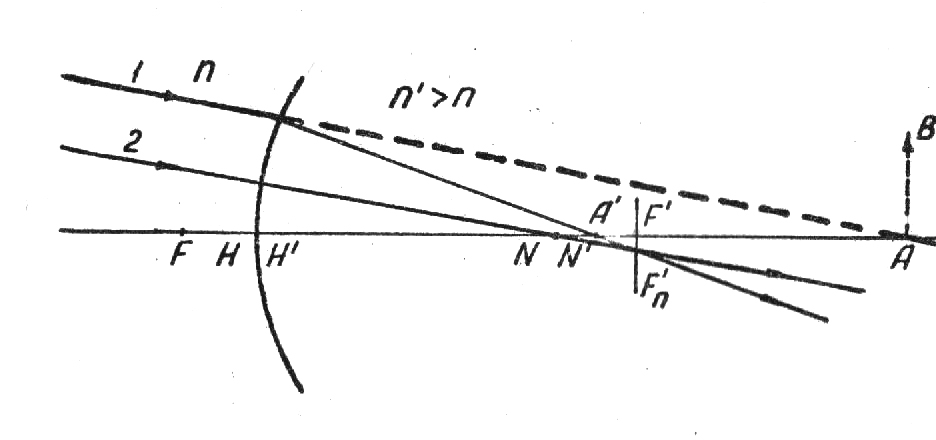

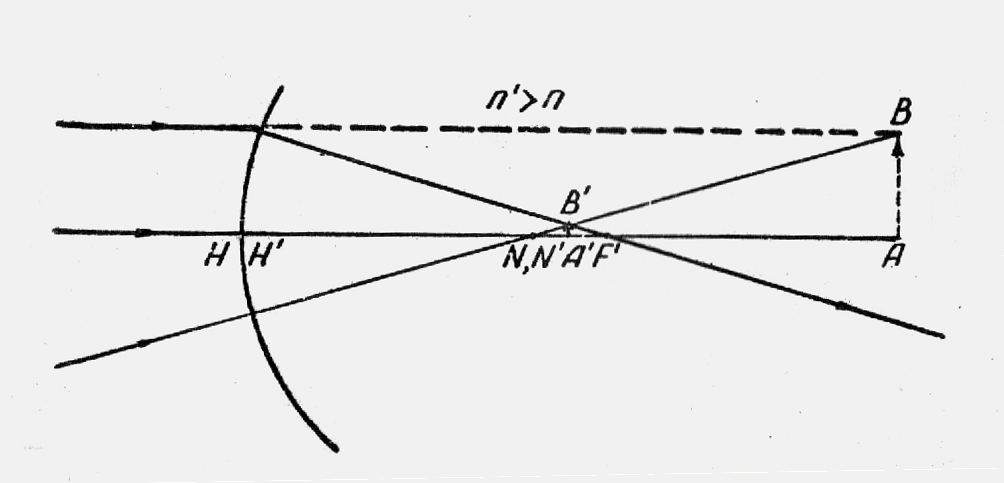
Рис. 5г

изображения точек мнимого предмета АВ.

Отношение поперечных размеров изображения к сопряженным с ними размерам предмета называется линейным поперечным увеличением  :

, (4.1)

где y’ = A’B’ , y = AB. Из рис.5б имеем:

откуда

Выражая r через а и a‘ из формулы для сферической границы (2.3), окончательно получим, что (4.2)

Из соотношения (З.6) также имеем, что (4.2а).

Несложно показать, что рассеивающая линза в воздухе всегда дает только мнимое (a’0 ), прямое (>0), уменьшенное ( ) изображение действительного (а<0) предмета. Собирающая линза дает прямое и уменьшенное изображение только для мнимого (a>0) предмета, при этом само изображение оказывается действительным (рис. 5г). Поперечное увеличение изображения действительного предмета, даваемое собирающей линзой, может принимать любые значения: положительные, отрицательные, больше и меньше единицы в зависимости от расположения предмета относительно линзы. В случае мнимого изображения показатель преломления пространства изображения относится к той среде, через которую проходят действительные преломленные лучи.

Две сопряженные плоскости, для которых  =1, называются главными плоскостями. Из сказанного выше следует, что равенство  =+1 возможно, если предмет мнимый (a > 0 , a’ > 0) или изображение мнимое (a < 0 , a’ < 0), причем абсолютные величины a и a’ стремятся к нулю. Следовательно, для сферической преломляющей границы главные плоскости совпадают и касательны к поверхности границы в точке Н (H’). Главные плоскости всегда перпендикулярны оптической оси и в общем случае не совпадают друг с другом. Точка пересечения H передней главной плоскости с оптической осью называется передней главной точкой, а сопряженная с ней точка Н’, лежащая на пересечении задней главной плоскости с оптической осью, называется задней главной точкой.

На рис.6 показан предмет в виде треугольника АВС и его изображение А’В’С’. Направим луч АД вдоль гипотенузы АС. Отношение

(4.3)

н азывается угловым увеличением.

Рис. 6

Из рис.6 в параксиальном приближении имеем:

(4.4)

Сравнивая выражения (4.2) и (4.4), получим, что

(4.5)

В частном случае, для оптической системы в однородной среде (n’ = n) .

Например, телескоп дает уменьшенное изображение Луны (<< 1) при очень большом угловом увеличении ( >>1). Последнее условие необходимо для разрешения близких друг к другу деталей изображения предмета, находящегося на большом расстоянии.

Сопряженные точки, для которых =1, называются узловыми точками, а плоскости, проходящие через узловые точки и нормальные к оптической оси, называются узловыми плоскостями. Для лучей, проходящих через узловые точки, u = u’, т.е. такие лучи после преломления в системе не изменяют своего первоначального направления. У сферической преломляющей границы обе узловые точки сливаются в одну и совпадают с центром кривизны поверхности N.

Фокусы, главные и узловые точки являются кардинальными точками оптической системы. У оптической системы, находящейся в однородной среде (n = n’) узловые и главные точки совпадают друг с другом ( =  =1).

Продольным увеличением  называется отношение продольных размеров изображения к сопряженным с ними продольным размерам предмета:

(4.6)

Из рис.6 имеем, что

, (4.7)

Сравнивая (4.5) и (4.7), получим, что

(4.8)

Таким образом, продольное увеличение всегда положительное. Отсюда следует важный практический вывод: при перемещении предмета вдоль оптической оси его изображение смещается в ту же сторону. Из рис.6 также видно, что треугольники АВС и A’B’C’ никогда не бывают подобными, т.е. с помощью рассматриваемых оптических систем нельзя получит неискаженное пространственное изображение. В параксиальных лучах можно получить практически неискаженное изображение предмета, расположенного в вертикальной плоскости.

Наряду с рассмотренными выше коэффициентами увеличения ,  и  для оптических систем, включающих и глаз наблюдателя, вводится понятие видимого увеличения Г. Видимым увеличением называют отношение тангенса угла, под которым глаз наблюдателя видит изображение, образованное оптической системой и расположенное на расстоянии наилучшего зрения L₀ от передней главной плоскости глаза, к тангенсу угла, под которым наблюдатель видит предмет невооруженным глазом (рис.7):

(4.9)

Рис.7

Обычно линейным увеличением характеризуют масштаб изображения проекционных объективов. Масштаб изображения зрительных труб (телескопических систем) и микроскопов характеризуют видимым увеличением.