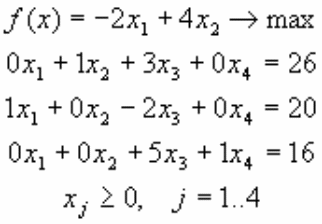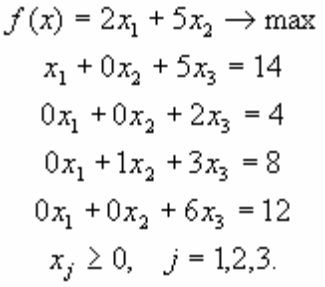Лабораторная работа № 3. Решение задач линейного программирования на основе табличного процессора ms Exсel.

Тема работы: Решение задач линейного программирования в электронной таблице Excel

Цель работы: Отработать методику решения задач ЛП в электронной таблице Excel.

Bведение

Решение задач линейного программирования с помощью инструментального средства “поиск решения ”табличного процессора MS Exсel

Задачи линейного программирования решаются в Excel с помощью инструментального средства “Поиск решения”. Процедуру поиска решения можно использовать для определения значения влияющей ячейки, которое соответствует экстремуму зависимой ячейки ѕ например, расходы на рекламу, обеспечивающие максимальную прибыль. Влияющая и целевая ячейки должны быть связаны формулой листа, иначе при изменении значения одной ячейки не будет изменяться другая.

Изменять условия и варианты поиска решения для линейных и нелинейных задач, а также загружать и сохранять оптимизируемые модели можно с использованием диалогового окна “Параметры поиска решения”.

Рассмотрим функции данного окна подробнее.

Для ограничения времени, отпускаемого на поиск решения задачи, служит одна из функций параметров - Максимальное время. В поле можно ввести время (в секундах) не превышающее 32767; значение 100, используемое по умолчанию и подходит для решения большинства простых задач.

Для управления временем решения задачи, путем ограничения числа промежуточных вычислений служит функция Итерации. В поле можно ввести время (в секундах) не превышающее 32767; значение 100, используемое по умолчанию, также подходит для решения большинства простых задач.

Для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам служит функция Точность. Поле должно содержать число из интервала от 0 (нуля) до 1. Низкая точность соответствует введенному числу, содержащему меньшее количество десятичных знаков, чем число, используемое по умолчанию ѕ, например, 0,0001. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.

Для задания допуска на отклонение от оптимального решения, если множество значений влияющей ячейки ограничено множеством целых чисел служит такой параметр как Допустимое отклонение. При указании большего допуска поиск решения заканчивается быстрее.

Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле Сходимость, поиск прекращается. Сходимость применяется только к нелинейным задачам, условием служит дробь из интервала от 0 (нуля) до 1. Лучшую сходимость характеризует большее количество десятичных знаков ѕ, например, 0,0001 ѕ – это меньшее относительное изменение, чем 0,01. Лучшая сходимость требует больше времени на поиск оптимального решения.

Для ускорения поиска решения линейной задачи оптимизации или линейной аппроксимации нелинейной задачи служат параметр Линейная модель.

Для приостановки поиска решения и для просмотра результатов отдельных итераций служит команда Показывать результаты итераций.

Для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине ѕ например, максимизация прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей служит установка Автоматического масштабирования.

Установка параметра Значения не отрицательны позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых она не была указана в поле Ограничение диалогового окна Добавить ограничение.

Для указания метода экстраполяции ѕ линейная или квадратичная ѕ используемого для получения исходных оценок значений переменных в каждом одномерном поиске служит функция Оценка, которая в свою очередь может быть:

Линейной – для использования линейной экстраполяции вдоль касательного вектора.

• Квадратичной – для использования квадратичной экстраполяции, которая дает лучшие результаты при решении нелинейных задач.

Для указания метода численного дифференцирования ѕ прямые или центральные производные ѕ, которые используются для вычисления частных производных целевых и ограничивающих функций служит параметр Производные:

Прямые – для гладких непрерывных функций.

• Центральные – для функций, имеющих разрывную производную. Не смотря на то, что данный способ требует больше вычислений, он может помочь при получении итогового сообщения о том, что процедура поиска решения не может улучшить текущий набор влияющих ячеек.

Установка параметра Метод:

Ньютона служит для реализации квазиньютоновского метода, в котором запрашивается больше памяти, но выполняется меньше итераций, чем в методе сопряженных градиентов.

• Сопряженных градиентов – для реализации метода сопряженных градиентов, в котором запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и необходимо экономить память, а также, если итерации дают слишком малое отличие в последовательных приближениях.

Параметр Загрузить модель служит для отображения на экране диалогового окна. Загрузить модель, в которой можно задать ссылку на область ячеек, содержащих загружаемую модель.

Установка параметра Сохранить модель неоходима для отображения на экране диалогового окна Сохранить модель, в котором можно задать ссылку на область ячеек, предназначенных для хранения модели оптимизации. Данный вариант предусмотрен для хранения на листе более одной модели оптимизации ѕ; первая модель сохраняется автоматически.

При поиске оптимальных решений смысл этих параметров знать не обязательно, так как их значения и состояния элементов управления, используемые по умолчанию, подходят для решения большинства задач. Все необходимые сведения о параметрах и командах, вводимых в этом диалоговом окне, можно получить, вызвав справку. Основные параметры, смысл которых очевиден, а их назначение не требует специальных знаний, приведены ниже:

максимальное время по умолчанию = 100;

• предельное число итераций = 100.

Если этих значений для нахождения решения окажется не достаточно, то на экране появится соответствующее сообщение, после чего вычисления можно повторить при тех же параметрах без их повторного назначения. В качестве относительной погрешности используется по умолчанию величина 0,000001, обеспечивающая достаточно высокую точность решения. Заметим, что снижение точности уменьшает число итераций и сокращает время поиска решения.

После успешного завершения поиска оптимальных решений на экране появится диалоговое окно “Результаты поиска решения”. С помощью него можно вызвать отчеты трех типов:

отчет по результатам (состоящий из трех таблиц: сведения о целевой функции, значение переменных, результаты оптимальных решений для ограничений и граничных условий);

• отчет по пределам (состоящий из двух таблиц: значение x в оптимальном решении, нижние пределы изменения значения x);

• отчет по устойчивости (состоящий из двух таблиц: значение для переменных (результат решения задачи, нормированный градиент, величина приводимая при выборе некоторых методов в диалоговом окне, параметров поиска решения), величина стоимости, множитель Лагранжа).

Таким образом, с помощью выше изложенных функций можно решать большинство задач математического программирования.

Задание к работе:

Ниже даны задачи линейного программирования, составленные в различной форме. Надстройка "Поиск решения" в электронной таблице Excel не является критичной к виду задачи, поэтому допускается использовать условия, приведенные в задачах без их изменения. В приведенной требуется решить по 6 задач из приведенных в задании. Условно все задание можно поделить на 2 варианта. Столбец 1, то есть, задачи 1,3,5,7,9,11 – вариант 1, столбец 2, то есть, задачи 2,4,6,8,10,12 – вариант 2.

Задача1. f(x) = x1 + 9x2 + 5x3 + 3x4 + 4x5 + 14x6  min x1 + x4 = 20 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi  0, i= 1,..,6	Задача2. f(x) = x1 - x2 - 3x3  min 2x1 – x2 + x3  1 4x1 – 2x2 + x3  -2 3x1 + x3  5 xi  0, i= 1,..,3
Задача3. f(x) = x1 - x2 +1  min xi  0, i= 1,..,3	Задача 4.
Задача 5.	Задача 6.
Задача 7.	Задача 8. f(x) = 2x1 - x3 + 3x4  max xi  0, i= 1,..,4
Задача 9. f(x) = 4x1 - 2x3 + 3x4 –9x5  max 3x1 + 8x2 +23x4  329 16x2 + 23x3 + x4  16 12x1 +13x2+14x3  980 xi  0, i= 1,..,5	Задача 10. f(x) = 270x1 + 13x2 + -19x3 –x5  min 2x1 + 6x2  500 15x3 + 6x5  214 29x2 + 37x3 + 18x4  22 210x1 +221x2+447x3  1298 xi  0, i= 1,..,5
Задача 11. f(x) = 3x2 - 170x3 + 111x4 – 26x5  min 3.6x1 + 6.6x3  28.9 11.5x4 + 2.3x5  214 32x3 + 1.8x4  160 2x1 +2x2+4x3 +7x5  94 xi  0, i= 1,..,5	Задача 12. f(x) = 492x1 – x2 + 3x3 –40x4  max 1.5x3 + 6.6x5  3.2 1.2x1 +1.3x2+3.1x3 = 26.6 3.2x3 + 21.8x4  38 6x3 +7.8x5  83 xi  0, i= 1,..,5