4.5. Лучистый теплообмен

МЕЖДУ ДВУМЯ АБСОЛЮТНО ЧЕРНЫМИ ПОВЕРХНОСТЯМИ

Между поверхностями, расположенными так, что они «видят» друг друга, происходит лучистый теплообмен, причем каждая из поверхно­стей излучает энергию на другую и поглощает энергию, излученную этой поверхностью. Для двух абсолютно черных поверхностей, нахо­дящихся при различных температурах и расположенных в непогло-щающей среде, результирующий обмен энергией выражается так:

<Э - <?!-, -0,-1 - о₀ {П-Т\)Р₁ «р,, _ <1 = о₀(П-П) Р_ж<р_Р,-._Р1 Вт, где ^>

Ч>р,—р, (аналогичное определение и для ф^-/?,) представляет собой уг­ловой коэффициент излучения поверхности 1 по отношению к поверх­ности 2. Он показывает, какая доля энергии, излучаемой поверх­ностью Р_г, попадает на поверхность Р₂. Полная энергия, излучаемая в единицу времени с поверхности 1 на поверхность 2 и наоборот, опре­деляется выражениями

<Э₁_₂ = о₀7₁Лф^,Вт (4.26)

(4.23)

84

Рав енство

<г₂-1 = *о71^Ф^-^ Вт.

(4.27) (4.28)

представляет собой соотношение взаимного лучистого обмена между поверхностями.

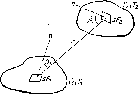
Рис. 4.4. Лучистый теплообмен между дву­мя поверхностями

Значения углового коэффициента излучения для метрических конфигураций представлены в табл. 4.3.

двух гео-

4.6. Применение алгебраического метода для определения угловых коэффициентов излучения

Выражения для угловых коэффициентов излучения систем из двух черных поверхностей, приведенные в табл. 4.3, можно с помощью алгебраического метода использо­вать для многих других геометри­ческих систем. Этот метод основан на принципе сохранения энергии и соотношений взаимного обмена для диффузных поверхностей.

Таким образом, неизвестный угловой коэффициент излучения можно определить, прибавляя или вычитая известные коэффициенты для тел сравнимых конфигураций. Один из примеров приведен на рис. 4.5. В табл. 4.4 перечислены определенные таким образом уг­ловые коэффициенты излучения для некоторых геометрических систем излучения.

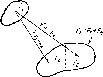
Рис. 4.5. Пример, иллюстрирующий применение алгебраического метода для определения углового коэффици­ента излучения

85

Угловые коэффициенты излучения для двух диффузно отражающих поверхностей

Таблица 4.3

Определение условии лучистого теплообмена

/. Излучение от элементарной площадки ёР_г падает на ограниченную поверхность Р_ш

Угловой коэффициент излучения у_ар

Г сов р_г сов р_а

ар_%

Поток излучения Л2 = а₀ (Т{ — Г*) аР_х уар₁_р₁ Соотношение взаимного обмена ^р1^<Рар₁^.р_г = ЛР₂Ц>₍1р₁—р₁

2. Излучение от ограниченной поверхности Р_х падает на ограниченную поверхность Р_г

Угловой коэффициент излучения

^{] I" |* соз рх соз р2}

9р

яг*

^Г1 р, р,

ОРцйР*

Поток излучения (? = ст„ (Т\— Т\) Р^ ф_/?]_^₁

Соотношение взаимного обмена Р\^р₁-.р_г — РзЧ'р^р, Р₁₍ Р_г — площадь поверхности 1 и 2 соответственно, м*; Т_±, Т₂ — абсолютная температура поверхностей 1_и 2 со­ответственно, К-

№ п. и.

Описание системы

Схематическое представление

Выражение для углового коэффициента излучения

Излучение от элементарной площадки а"Р_1г падающее на ограниченную поверхность Р_г

Площадка а"Р] параллель­на прямоугольной плоско­сти

в

с в \

УГ+С2 ^сЬ*у\ + &у

	1
2	Площадка а'Р1 и прямо­угольная плоскость распо­ложены относительно друг друга под углом Ф	Ь/ с / \Ф/ Ъ /	<РсР,-Р, = В + -^(С созф-1) с1«|- + где В-—Ь/а; С=с/а;
		С	Х = У1+С*—2Ссо8</>; У^~\/В* + 5\п*Ф
3	Сферический точечный источник ЙР| расположен относительно прямоуголь­ной плоскости под углом ф	с	1 Г Г В(С-созф) ]^ ЧлРх-г» 4п Г ё1Ув*+С*+\-2Ссс*фГ 1 В С05 ф \) где В = Ь/а; С —с/а
4	Площадка АР, парал­лельна круглому диску		1 Г 1+С2 — В* ] Ф<-/\-,р, 2 [' т/(14-В2-г-С2)2 —4В2Са ]' где В =Ь/а; С —с/а
5	Площадка а~Р\ перпенди­кулярна круглому диску	0е{?1	1 Г ^Вг+С* 1 ЧйРг-Рг 2с[У(1-г-В2+С2)2—А(?В*-\\' где В = Ъ/а^ С = с/а

Продолжение табл. 4 .3

№ п. п.	Описание системы		Схематическое представление		Выражение для углового коэффициента излучения
6	Узкая полоса с1Р\ и не­ограниченно длинный ци­линдр		щ 1 мм		аЬ
7	Площадка а~Р{ на поверх­ности цилиндра н неограни­ченная плоскость		I I ! * о-*--1--		Ф<Я»,-Р,= "|~(1+С08 6)
8	Внутренний кольцеоб­разный слой ЛРх и торец по­лого цилиндра		н—^-н		1 / С*+2 \ где С — с/а
9		Площадка а"р1 около тор­ца цилиндра, параллельная его оси		V-с--И 1 1		1 Г С , \Х*—2В *«*-*-^*уШ=Г+с[ ху х Хсх8^1/1Ы_с1е л/'Щ], У V В + 1 ё V В + 1}Г где В=Ыа; С=с/а; Х = У(1 + ВУ + С* ; У = У(1—В»)»+-С*
10		Площадка йР\ параллель­на эллиптическому диску		^^7 1 1С		аЬ
11		Линейный источник а~Р\ параллелен прямоугольной плоскости		^#7 / у у		С{еС+У1 + С*СЧу1 + С2)]' где В = Ь/а; С = с!а

Продолжение табл. 4.3

К» п. п.

Описание системы

Схематическое представление

Выражение для углового коэффициента излучения

Лииейиый источник а"Р\ и прямоугольная плоскость расположены относитель­но друг друга под углом ф

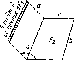
1 Г , „ , «п»Ф. Г В* + Х² ]

51П 2 ф Г Я . /С— СОЗ ф \~\

■[7-* + с*8|—Г" 11 +

2В

51П ф

КГ (С— С05ф\ /С05 ф \1

X соз'ф +

к

С соз ф—1

с1ё

X \ X

где В = 6/а; С = с/а;

Х=УС²—2 С соз ф+1; К = УВ² + з'п² ф

Площадка с?^, образует угол Ф с прямоугольной пла­стиной, к верху которой до­бавлена пластина треуголь­ной формы

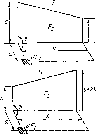
с-кЬ

. , „ С соз Ф — 1 I- Ф^-Р, = Т- с1§В +---X

X

— с(й

2 я I к

(6²4-1)В + 6(С—созф) К