3 Основные формулы и данные по теплообмену

Рис. 3.1. Коридорное распо­ложение труб

		о
о	о
о	о	о
о	о	о

Рис. 3.2. Расположение труб в шахматном порядке

О О

_{о о}

Некоторые данные по Ар для труб с различным поперечным сече­нием приведены в табл. 3.3.

Для обеспечения движения жидкости по трубе должна подво­диться внешняя энергия. При этом часть подводимой от внешнего ис­точника энергии, которая составляет АрV_т8 Вт, компенсирует поте­рю давления.

3.8. Каналы и трубы

Знание закономерностей нагрева и охлаждения при протекании жид­кости через трубы имеет большое значение для инженеров. Если для заданной геометрии системы и для определенных условий движения потока коэффициент теплоотдачи известен, то тепловой поток может быть определен из уравнения

0 = аР(*_СТ—(_ж), Вт,

(3.15)

где 1_Ж — температура смешения жидкости.

Для внешних задач в качестве температуры свободного потока может быть использована температура смешения. В каналах и трубах эту температуру можно определить только при условии, если извест­но распределение температуры. К сожалению, определение распре­деления температуры сопряжено с большими трудностями. Поэтому используют среднюю логарифмическую разность температур, которая определяется только на основании известной температуры жидкости на входе и выходе и является гораздо более удобным и подходящим параметром.

Среднелогарифмическая разность температуры определяется урав­нением

(^ст ^>к)вх—(^ст ^ж)вьи

(3.16)

1п [(/_Ст—^к)»х/('ст— ^к)вых]

Таким образом, тепловой поток можно рассчитать по формуле <Э = аРЫ_1т Вт, (3.17)

где а — среднее значение коэффициента теплоотдачи.

58

Это же уравнение дает возможность найти необходимую поверх­ность трубы прн определенном значении плотности теплового потока и при заданном температурном перепаде.

Если известно значение температуры 1_п;,х для одного из попереч­ных сечений трубопровода, то значение температуры ^_к,₂ в другом сечении, расположенном на расстоянии / от первого, можно опреде­лить из следующего уравнения:

аР1 +2и_т Ср 5

где Р и 8 — периметр и площадь поперечного сечения трубы соответ­ственно; и_т — массовая скорость; ос — среднее значение коэффициента теплоотдачи на длине /. Массовая скорость и_т может быть оценена как

ч_т = <2т/5 = ру, где V— средняя скорость потока. _

В табл. 3.4 перечислены соответствующие зависимости Ыи, по ко­торым может быть рассчитано среднее значение коэффициента теплоот­дачи ос для движущегося потока жидкости в трубах с различной гео­метрией сечения.

3.9. Теплоотдача при внешнем обтекании тел

Этот раздел посвящен теплообмену при омывании вынужденным пото­ком жидкости плоских поверхностей (т. е. плоских пластин) и труб, расположенных перпендикулярно к направлению движения потока. Плоская пластина для анализа представляет собой простейшую гео­метрическую фигуру, поэтому она тщательно изучена. Результаты та­кого анализа весьма полезны также и потому, что многие из получен­ных выводов могут быть распространены на хорошо обтекаемые тела, начальные участки труб, клинья, конические тела и на любые поверх­ности плоского типа. Используя модифицированную Кольбарном ана­логию Рейнольдса, можно получить классические результаты. Обоб­щенные результаты значительного количества экспериментальных ис­следований приведены в табл. 3.5.

Ввиду сложного характера движения жидкости при обтекании тел, имеющих сферическое или цилиндрическое сечение, получение ана­литического решения связано с очень большими трудностями. Для этого приходится прибегать к эксперименту и к методу анализа размерностей. Коэффициент теплоотдачи при обтекании сфер воздуш­ным потоком рекомендуется определять по следующей формуле [3.201:

0,37 (Ке)⁰-⁶ для 17 < Ке < 7 • 10»,

где диаметр сферы принят за характерный размер.

В табл. 3.6 и 3.7 представлены некоторые данные по конвектив­ному теплообмену при обтекании вынужденным потоком жидкости цилиндров с различным сечением и пучков труб.

3*

67

Таблица 3. 4

Теплообмен при вынужденном движении жидкости в цилиндрических трубах с различным поперечным сечением

Формула: N11 = а.в1\ = СКе^т-Рг"/С. Обозначения: _Не = ру/З/ц; Рг = ЦСр /X;

а — средний по длине трубы коэффициент теплоотдачи, Вт/ (м².° С);

К — коэффициент теплопроводности жидкости, Вт/ (м-^сС)

р — плотность жидкости, кг/м³; с_р — удельная теплоемкость жидкости, Дж/(кг-°С);

\х — динамическая вязкость жидкости, Н-с/м²; V_т — средняя скорость жидкости, м/с; <2_т — массовый расход жидкости, кг/с;

Р — площадь поверхности нагрева трубы, м³; й — гидравлический диаметр, м; Р — периметр сечения, м; 'ст — температура стенки трубы, ° С.

Значения величии р, Я,, ц берутся прн температуре сме­шения 1_т = (<_ж. _вх + 'ж. выхУ², где 'ж. вх, 'ж. вы: — темпе­ратура жидкости на входе и выходе соответственно, С. Тепловой поток можно определить из выражения <Э = аРМ_1т = ШкРЫ_1гп10 Вт, Где ^ Ост— ^ж)вх — Ост— ?ж)вых

1п [(<_ст — <ж)вх/0ст— 'ж)вых] — среднелогарифмическая разность температуры, С.

Форма поперечного сечения

Режим течения

Круглая труба

й

а

1,860

3,660

0,023 0,027

3

о

0,8 0,8

1^ 3

0

0,4 0,33

Ч \Цст / 1

1

Л. И-ст

0, 14

Ламинарный поток в короткой трубе, Ке<2000, О2>10

Ламинарный поток в длинной трубе, Ке<2000, Сг<Ю

Турбулентный поток га­зов, Ке>2000

Турбулентный поток жидкости с большой вяз­костью, 0,6<Рг<100

Прямоугольная Ь труба

ь
	а	2,98	0	0
1,4	1,17 а	3,08	0	0
2	1,33 а	3,39	0	0
3	1,5 а	3,96	0	0
4	1.6 а	4,44	0	0
8	1,78 а	5,95	0	0
со	2,0 а	7,54	0	0

1

Ламинарный поток Ке<2000

То же, Ке<2000 » » Ке<2000 » » Ке<2000 » » Ре<2000 » » Ке<2000 » > Ке<2000

3	Продольн параллельнь и- ' -Я		м разрез или 1е пластины 1 1 1	26 26		1,85 7,54		1 3 0		1 3 0		1		Ламинарный поток, Ке<2000, / 2б\ / Ке- Рг-1>70 ^Ке -Рг^у|<70
4	Равносторонний тре­угольник А				0,58 а 0,58 а		1,30 2,47		1 3 0		1 3 0		|0,58 о^/з 1		Ламинарный поток, Ке<2000, / 0,58 а\ „ Ке- Рг-—1>7 / 0,58 о\ „ Ке- Рг-— 1<7
5	пласт 6	параллельные нны [ у////////////// стина изолирована			46		4,86		0		0		1		Ламинарный поток

Литература: [3.6, 3.9, 3.20, 3.22, 3.25, 3.27].

Таблица 3.5

№ п.н.	Движение жидкости вдоль плоской поверхности	Формулы			Режим течения
1	Невозмущенный режим течения		= 0,332 Ке'/2	• Рг'/3 (локальное значение)	Ламинарный поток,
			= 0,664 Ке]/2	• Рг1/3 (среднее значение)	Ке < 5-Ю5, 0 <х < /
	'///>//////>/////////////,>;;>;//,	Ииж	= 0,029 Ке4/5 = 0,037 Ке4/5	Рг'/3 (локальное значение) Рг'/3 (среднее значение)	Турбулентный потек, Ке > Ь-105, 0 < х < 1

Формула: (2= аР 0_СТ - 1„) Вт. Обозначения:

^_х — ах/Х — локальное значение числа Нуссельта в точ­ке х;

№и_х = ах/'к —среднее значение числа Нуссельта для площа­ди поверхности нагрева, простирающейся на расстояние х от края пластины; Ке_ж = ршг/ц; Рг = цСр/А;

р — плотность жидкости, кг/м³;

Решения задач конвективного теплообмена прн омыванни плоских пластин вынужденным потоком жидкости

|х — динамическая вязкость жидкости, гЬс/м⁸; Ср — удельная теплоемкость жидкости, Дж/ (кг-°С); X — коэффициент теплопроводности жидкости, Вт/ (м- °С);

р — площадь поверхности нагрева, простирающей­ся иа расстояние х, и¹; V — скорость свободного потока, м/с; / — длина поверхности, м.

х — расстояние, измеренное от передней кромки, м.

Значения свойств взяты при средней температуре погра­ничного слоя жидкости 1_т = (<_ст + <_ж)/2.

Смешанный режим течения

Ламинарный поток

Тур5улентный поток

Стенка нагревается частично ^х ~&ст

1г

-X

Среднее значение №1_ж на длине 0 < х <1 №1*= 0,037 Рг¹/³ (Ке*^/5—С), где С = 23 500 для (Р_че)_Кр = 5-10⁵; С=14 200 для (Ке)_кр = 3-10»; С = 4300 для (Р_че)_Кр = 10»

Ламинарный поток на длине 5, где критерий Рейнольдса до­стигает критического значения (Ке)цр, и далее для доз тур­булентный поток

№1_Я = 0,332 КеУ² Рг¹/³ ное значение)

Ш_х = 0,664 КеУ² Рг¹/³ (среднее значение)

Ми_ж=0,029 [Ке*/⁵ Рг¹/³ (локальное значение)

№_ж = 0,037 Ке*/⁵ Рг¹/³ (среднее значение)

_1

³ (локаль-х

I \ »

1-Ь х

Ламинарный поток

Ке < 5-Ю⁵, 1₁<х<1₂

Турбулентный поток

Ке > 5-10«, 1_1<х<1₂

Таблица 3.6

Форма сечения		с	т	Интервал значений Ке	Характерный раамер X
-о:	й	0,437 0,565 0,800 0,795 0,583 0,148 0,0208	0,0895 0,136 0,280 0,384 0,471 0,633 0,814	10~4—4-10-3 4. Ю-3—9-Ю-2 9.10-2—1 1—35 35—5-103 5-103—5-Ю4 5.10*—5-Ю5	й (1 (1 (1 (1 (1 (1
		0,178 0,102	0,699 0,675	2,5-Ю3—8-103 5-103—105	4а я 4а л
	а
		0,290 0,246	0,624 0,588	2,5-Ю3—7,5-Ю3 5.Ю»—105	4а я 4а_ я
-о		0,160 0,039	0,638 0,782	5-Ю3—1,95-104 1.95.104—105	6а я 6а я

63

Теплоотдача при поперечном омываиии воздушным потоком цилиндров с различной формой сечения

Формулы:

_ N11 = СКе^ш — для цилиндра круглого сечения;

_ = 0,43 + С Ке^т — для цилиндров с другими формами сечения;

Ыи = 0,43 -4- СКе^шРг⁰-³¹ — при омывании жидкостью;

0. = гТй ХР {(_ст — (_Ж)/Х.

Обозначения:

Ш = а.Х1Х\ Ке = роЛУц; Рг = с_рц/Х; р — плотность жидкости, кг/м³; р. — динамическая вязкость жидкости, Н ■ с/м²; с_р — удельная теплоемкость, Дж/(кг ■ °С); а — среднее значение коэффициента теплоотдачи, Вт/(м² • °С); X — коэффициент теплопроводности, Вт/(м ■ °С); Р — площадь поверхности, м²; 'ст — температура стенки, °С; 1_т — температура смешения жидкости, °С. Предполагается, что поверхности стенок ровные. Значения свойств взяты при средней температуре пограничного слоя жидкости (_т = (?_сх + (ж)/2.

Продолжение табл. 3.6

Форма сечения					с		т		Интервал значений Ке		Характерный размер X
-Г?					0,153		0,638		5-10»—1 О5		6а Л
		н		2а		0,293		0,660		3-Ю3—2-104	6а л.
					0,248		0,612		2,5.Ю3—1,5-Ю*		У 2 (а2-^2)
-о:				Ь		0,094		0,804		3-Ю3—1,5-10*	V 2(а2+Ь2)
				/ /		0,276		0,610		3-Ю3—2-10*	1,09а
		а _1	г		0,227		0,731		4-103—1,5-10*		2а л

Литература: [1.3, 3.1, 3.18, 3.22, 3.25, 3.26, 3.30].

64

Таблица 3.7

Теплоотдача при поперечном омывании жидкостью пучков труб Формула:

гТй = СКе⁰.«Рг°.³ (|г/р_Ст)°.¹⁴. Обозначения:

N11 = а'а/х; Ке == роаУр; Рг = рс_рА;

а — среднее значение коэффициента теплоотдачи, Вт/(м² . °С); р — плотность жидкости, кг/м³; р. — динамическая вязкость жидкости, Н • с/м²; М-ст — динамическая вязкость жидкости при <_ст, Н « с/м²; ср — удельная теплоемкость при постоянном давлении, Дж/(кг » °С); Л — коэффициент теплопроводности жидкости, Вт/(м . °С); о — скорость невозмущенного потока, м/с; й — диаметр трубы, м. Значения параметра С, приведенные ниже, взяты из работы [3.91. Они при­менимы для значений 2000 < Ке < 4 • 10⁴.

Значения величин взяты при средней температуре пограничного слоя жидкости (_т = (/_ст + /_ж)/2.

Рис. 3.3. Коридорное рас­положение труб

-гО ООО

_{~~^о ООО}

Значения параметра С

v-

О О О О

_{о о о о}

и л	и/4
	1.25	2	3	4
1,25	0,888	0,890	0,880	0,835
2	0,613	0,613	0,638	0,632
3	0,427	0,427	0,500	0,504
4	0,356	0,356	0,421	0,421

Рис. 3.4. Расположение труб в шахматном по­рядке

Значения параметра С

v-

то			о
хо	о
			о
о	о
			о
о	о
			о
а
		1,25			2	3		4
1,25		0,953			0,937	0,875		0,812
2		0,686			0,669	0,638		0,611
3		0,559			0,544	0,506		0,500
4		0,489			0,488	0,466		0,442

66

3.10. ТЕПЛООТДАЧА ПРИ высоких СКОРОСТЯХ

При достаточно высоких скоростях движения потока жидкости нали­чие сил трения является причиной значительного повышения темпе­ратуры пограничного слоя. Для очень больших скоростей потока изменения температуры по сечению пограничного слоя могут быть весьма значительными. Это явление аэродинамического нагрева особенно проявляется в авиации и ракетной технике при сверхзвуко­вых скоростях движения. В этих условиях тепло от нагревающегося пограничного слоя передается непосредственно твердой поверхности. Для представления температуры пограничного слоя принято ис­пользовать характерную температуру Т_г, называемую температурой восстановления (или температурой адиабатной стенки). Достижение стенкой температуры восстановления свидетельствует о том, что отсутствует какой-либо теплообмен, обусловленный конвективной теплоотдачей. В этом случае плотность теплового потока может быть рассчитана по формуле

где — скорость невозмущенного потока.

Коэффициент восстановления температуры г является мерой эф­фективности процесса нагревания пограничного слоя и в значительной степени зависит от числа Прандтля в соответствии с тем или иным сформировавшимся режимом течения. Для плоской пластины (давление вдоль поверхности постоянно) коэффициент восстановления темпе­ратуры может быть определен из следующего выражения:

при ламинарном режиме г= Рг'/²;

при турбулентном режиме г= Рг'/³. (3.21)

Если г= 1, то температура восстановления становится равной температуре торможения. Для потока, движущегося с низкой ско­ростью (т. е. при V^₀I2с_рТо₀ < 1), Т_т практически равна температуре невозмущенного потока Г„, а при больших скоростях — температуре адиабатной стенки Г_от. В стационарных условиях температура стенки определяется из теплового баланса между теплом, поступающим к пограничному слою благодаря конвекции и падающему излучению, и теплом, рассеянным за счет поверхностной теплопроводности, излу­чения и других совместно действующих процессов охлаждения.

Известно, что свойства жидкости изменяются с температурой и давлением. При умеренно высоких скоростях потока могут быть полу­чены приближенные результаты путем отнесения * значений Этаких

Я,= а. (Т_г—Т_ст) Вт/м^а и температура восстановления — по формуле;

(3.19)

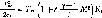
(3.20)

67

свойств, как р, р,, А, и с_р, к определяющей температуре Г*. Соответ­ствующее выражение, предложенное Эккертом [3.41], имеет вид

Т* = Гоо-4-0,5 (Г_ст - Г_то) + 0,22 (Т_г- Т«,) =

= 0,5 (Т_х + Т_сг) + 0,22 Л^±М²Г_ТОК. (3.22)

Прн этом удельную теплоемкость можно считать постоянной. Значение динамической вязкости можно определить с помощью соотношения Сазерленда:

М-о \ Го / \ 1+218/Г* )

где р,₀ — известное значение динамической вязкости при температуре

Го-Коэффициент теплоотдачи часто выражают через число Стантона, которое связано с коэффициентом поверхностного трения /_с. При омывании пластины ламинарным или турбулентным потоком это соот­ношение имеет вид

51=:-^-Рг-²/³. (3.24)

При очень высоких скоростях движения потока в пограничном слое возникает значительный перепад температуры, и предположение о по­стоянстве удельной теплоемкости неверно. Поэтому в формуле для рас­чета теплоотдачи температура не может служить определяющим параметром. Вместо температуры в таком случае используют энталь-т

пию газа, т. е. г — ^с_вс!Т. Значения свойств при этом следует опре-о

делять для температуры, отнесенной к соответствующему значению энтальпии I*. Выражение, предложенное Эккертом, имеет вид

I* = и + 0,5 (/_ст—и) +0,22 (1_т—1ео) = 0,5 (*„ + 1_Сг) +

+ 0,22г_г-1^!-М²1соДж/кг. (3.25)

При таком подходе плотность теплового потока определяется как

_Я$ = а_; (1_Г - г»,) Вт/м², (3.26)

где а_; = а (Т_г — Т_СГ)1(1_Г — 1_ст), и энтальпия восстановления 1_г

_1г = _{1м +} г_г^-Дж/кг. (3.27)

Перечень формул для расчета коэффициентов теплоотдачи через чис­ла Стантона и Нуссельта приведен в табл. 3.8.

67

Таблица 3.8

Характеристика	Для ПОСТОЯННОЙ Ср	Для переменной Ср
Плотность теплового потока, Вт/м2 Характеристическая температура, К, или	<7., = а(Гг —Гст) Г* = ГооН-0,5(Гст--7^ + 0,22 (Гг-Гм)	Яз — <Ь1 ('V — «ст)
характеристическая энтальпия, Дж/кг Температура восста­новления, К, нли энтальпия восстановле­ния, Дж/кг	7,г = 7,оо + "'»/2ср	'*='оо+0,5 (/сТ-/оо) + + 0,22 (/^-*во) /г = и + »'1»»/2

68

Формулы для расчета теплоотдачи при высокой скорости потока

Обозначения: а — коэффициент теплоотдачи, отнесенный к характеристической темпера­туре, Вт7(м² I °С);

а; — коэффициент теплоотдачи, отнесенный к характеристической энтальпии, кгЯм² • с);

(с ⁼ ^ст'О.^Р^от—коэффициент поверхностного трения (определяется анало­гично коэффициенту трения /); с_р — удельная теплоемкость при постоянном давлении, Дж/(кг . °С); М = Ооо/соо — число Маха;

х — расстояние, отмеренное от передней кромки, м; *ир ~ критическое расстояние перехода ламинарного потока в турбулентный; г — коэффициент восстановления температуры; г = (Т_г — Т_ст)/&1₀/2с_р) — выражен через температуру; г = (1_г — 1ст)1 — выражен через энтальпию;

Я — универсальная газовая постоянная [для воздуха Я — 287 Дж/(кг I К)]; р — плотность жидкости, кг/м³; н — вязкость жидкости, Н • с/м²;

А — коэффициент теплопроводности жидкости, Вт/(м-°С); Т

^{I = _[ СрйТ — удельная энтальпия, Дж/кг;}

Иоо — скорость невозмущенного потока, м/с; У^ят скорость звука в невозмущенном потоке, м/с; Т — абсолютная температура, К; у = Ср/Сц — отношение удельных теплоемкостен; 81* = а/р*с_рОоо = а_г/р*Уоо — число Стантона;

Рг* = с*р/А* — число Прандтля (значения при высоких температу­рах могут быть заимствованы из работы [3.46] или [3.47]);

Ке* = р'Ч'ооХ/и.* — число Рейнольдса; Ыи* = ах/К* — число Нуссельта. Индексы: I — энтальпия; оо — невозмущенный поток; г — восстановление; ст — стенка.

Верхний индекс (*) указывает на то, что значения свойств рассчитаны либо при характеристической температуре Г*, либо при температуре, соответствую­щей характеристической энтальпии I*.

Продолжен и е табл. 3.

Характеристика	Для постоянной ср	Для переменной ср
Коэффициент вос­становления температу­ры То же — энтальпии	г = (Рг*)1 ^—ламинар­ный поток	Г; = (Рг*)112 —ламинарный поток
	г=(Рг*)1/3—турбу­лентный поток	г; = (Рг)1/3 — турбулент­ный поток
Число Стантона /с — ^/з 51* = '-§- (Рг*)	51* = а/р*сг,У0О	51* = а(/р*Уоо

Формулы для плоской пластины

Локальное значение коэффициента поверх­ностного трения

Среднее значение ко­эффициента поверхно­стного трения

Число Нуссельта (Ш = 51-Ке-Рг)

Среднее значение а от

Л! = 0 ДО *>Хкр

/_с= 0,664 (Ре*)""¹/² (Польгаузен), ламинарный поток, Ре < 5-10⁵

/■_с = 0,0592 (Ре*)^-0-¹¹ (Блазиус), турбулентный поток, 5-10⁵ < Ре < 10⁷

/с= 0,288 (1оВюКе*)

-2.45

(Прандтль—Шлихтипг),

турбулентный поток, 5-10⁶<Ре<10⁹

1_С= 1,328 (Ре*)^-1/² (Польгаузен), ламинарный по­ток, Ре < 5-10^:>

/_с = 0,074 (Ре*)^-0,2 (Блазнус), турбулентный поток, 5-10'<Ре < 10⁷

7с= 0,455 (1обюКе*)^-2,58 (Прандтль—Шлихтинг), турбулентный поток, 5-10⁵<Ре< 10⁹

№1* = 0,332 (Ре*)^1/2 (Рг*)'/³ (Польгаузен), лами­нарный поток, Ре<5-10⁵

№1* = 0,029 (Ре*)^0,8 (Рг)¹/³ (Блазиус), турбулент­ный поток, 5-10⁵<Ре<10⁷

1Чи* = 0,144 Ре* (Рг*)^1/3/(1обю Ре*)²'⁴⁵ (Прандтль— Шлихтинг), турбулентный поток, 5-10⁵<Ре< 10^е

а = 0,036— (Рг*) х

1/3

[(р_е;)°.^з-(ре;_кр)°.ч

+ 18,5(Ре;_кр)⁰'⁵]

ламинарный поток при д: = 0 до х=х_кг>; турбулентный поток при л:>л!кр (Блазиус)