§3.6. Функция распределения для вырожденного газа бозонов

Функция распределения для вырожденного газа бозонов (Бозе-Энштейна) имеет вид:

(3.36)

Применим эту функцию для описания фотонного газа. Фотоны имеют ряд особенностей:

1. Масса покоя фотона равна нулю.

2. Все фотоны движутся с одной и той же скоростью (скоростью света с), но могут обладать различной энергией Е=ћω и импульсом р=ћω/с, зависящими от частоты ω.

3. Фотоны не сталкиваются между собой, поэтому равновесное распределение в фотонном газе может устанавливаться только в присутствии тела, способного излучать и поглощать фотоны.

4. Фотоны могут создаваться (при излучении) или уничтожаться (при поглощении) в любых количествах. Поэтому число фотонов в фотонном газе не является строго фиксированным и зависит от состояния газа.

Химический потенциал невырожденного газа всегда отрицательный и имеет довольно большое значение. Химический потенциал µ равновесного фотонного газа равен нулю, поэтому фотонный газ всегда вырожден. Полагая µ=0 формулу (3.36) можно переписать в виде (формула Планка):

(3.37)

Формула Планка выражает среднее число фотонов, обладающих энергией Е=ћω.

§3.7. Правила статистического усреднения.

Чтобы задать состояние коллектива частиц, надо указать термодинамические параметры, т.е. указать значения координат и составляющих импульса. Их выражают через усредненные характеристики отдельных частиц этого коллектива.

Рассмотрим коллектив частиц, состоящий из N одинаковых частиц, каждая из которых может принимать ряд значений энергии: E₁, E₂, , E_n. В какой-то произвольный момент времени каждая частица имеет какую-то энергию. В результате получаем набор чисел N(E_i), выражающий число частиц, имеющих энергию E_i. Чтобы определить среднюю энергию частиц, сложим энергии всех частиц и поделим полученную сумму на число частиц.

Полное число частиц N=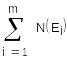 , а их суммарная энергия равна 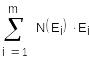, поэтому усреднение по коллективу производится по формуле (3.38).

Если энергия частиц может принимать непрерывный ряд значений, то в этом случае вместо числа частиц с данным значением энергии следует рассматривать число частиц с энергией, заключенной в интервале от E до E+dE (3.39).

Подобное усреднение можно произвести для любой физической величины М, являющейся функцией координат и импульсов частиц системы. Если М меняется непрерывно, то

(3.40)

Глава 4. Зонная теория твердых тел

§4.1. Основные положения

Для определения свойств кристалла нужно знать характер взаимодействия всех составляющих его частиц (ядер, электронов). Точное их описание практически невозможно из-за большого количества (≈10²⁸ в 1м³) и непрерывного движения.

Для описания многих свойств необходимо знать только состояния всех валентных электронов (многоэлектронная задача), что упрощает изучение свойств кристалла. Ряд дополнительных упрощений сводит многоэлектронную задачу к одноэлектронной задаче движения одного электрона в электрическом поле кристалла, что позволяет решить для этого случая уравнение Шредингера. Упрощения заключаются в следующем:

1) При описании движения электрона ядра считаются неподвижными (из-за очень большой разницы в массах и скоростях движения).

2) Медленное движение ядер рассматривается в поле среднего пространственного распределения заряда электронов (т.е. без учета поля, создаваемого мгновенным расположением электронов).

3) Взаимодействие каждого электрона с остальными рассматривается как взаимодействие его с усредненным пространственным распределением заряда электронов. Это поле создается усредненным в пространстве зарядом всех других электронов и всех ядер.

Таким образом, в рамках зонной теории многоэлектронная задача сводится к задаче о движении одного электрона во внешнем периодическом поле - усредненном и согласованном поле всех ядер и электронов.

Состояние электрона в атоме определяется пятью основными квантовыми числами:

- главное квантовое число (n=1; 2; 3…), определяющее энергию электрона в поле ядра (номер слоя);

- орбитальное квантовое число (l=0; 1; 2; 3…, соответственно s, p, d, f …), определяющее орбитальный момент количества движения электрона;

- магнитное квантовое число (m_l=0, 1; 2; 3;…l), определяющее ориентацию орбитального момента количества движения;

- спиновое квантовое число (s=1/2), определяющее собственный момент количества движения электрона;

- спиновое квантовое число (m_s=1/2), определяющее ориентацию собственного момента количества движения электрона.