§3.2. Невырожденные и вырожденные системы.

По характеру поведения в системе все микрочастицы можно разделить на две группы: фермионы и бозоны. Фермионы – это частицы с полу численным спином (электроны, протоны, нейтроны и т.д.). Бозоны – это частицы с целочисленным спином (фотоны, фононы и т.д.).

В системе фермионы обладают выраженным свойством «уединенности» - если данное квантовое состояние уже занято фермионом, то другой фермион, данного типа, не может находится в этом состоянии (принцип Паули). Бозоны, наоборот, стремятся к объединению. Они могут неограниченно заселять одно и тоже состояние, причем с тем большей вероятностью, чем больше бозонов находится в этом состоянии.

Предположим, что на N одинаковых частиц приходится G состояний, в которых может находится отдельная частица.

Условие невырожденности: N/G  1, (3.8),

т.е. число возможных состояний гораздо больше числа частиц. Такие системы называются невырожденными (например, идеальный газ).

Условие вырожденности: N/G  1 (3.9),

Такие системы называются вырожденными. Вырожденные системы могут образовываться только из квантово-механических объектов. Однако, квантово-механический объекты могут образовывать невырожденные системы, если выполняется соотношение (3.8)

Физическая статистика, изучающая невырожденные системы, называется классической статистикой – это статистика Максвелла-Больцмана.

Статистика, изучающая вырожденные системы, называется квантовой статистикой. Есть две квантовые статистики: квантовую статистику фермионов называют статистикой Ферми-Дирака; квантовую статистику бозонов называют статистикой Бозе-Эйнштейна.

Если уменьшить число частиц в системе или увеличить число возможных состояний, то вырожденная система превращается в невырожденную. В этом случае применяется статистика Максвелла-Больцмана.

Для того, чтобы задать состояние частиц, надо указать значение их координат и импульсов или энергию частиц, которая определяется координатами и импульсами. Связь между этими двумя типами величин осуществляет статистическая функция распределения, которая выражает число частиц с энергией от E до E+dE в системе, состояние которой описывается двумя термодинамическими параметрами:

N_,(E)dE (3.10)

Ее называют полной статистической функцией распределения ( и  обычно опускают). Она может быть представлена в виде произведения числа состояний g(E)dE, приходящихся на интервал энергии dE, на вероятность заполнение этих состояний частицами f(Е), т.е.

N(E)∙dE = f(E)∙g(E)∙dE (3.11).

f(E) называют просто функцией распределения (плотность). Ее можно трактовать как среднее число частиц, находящихся в данном состоянии.

Задача отыскания полной функции распределения частиц по состояниям сводится к отысканию функции g(E)∙dE, описывающей распределение состояний по энергиям, и функции f(E), определяющей вероятность заполнения этих состояний частицами.

§3.3. Число состояний для микрочастиц.

В классической механике состояние частиц определяется заданием трех координат (x, y, z) и трех составляющих импульса (p_x, p_y, p_z). Представим себе шестимерное пространство с осями координат XYZ и P_xP_yP_z. Состояние частицы в этом пространстве в каждый момент времени определяется точкой (x, y, z, p_x, p_y, p_z) такое пространство называется фазовым, а точки (x, y, z, p_x, p_y, p_z), определяющие состояние частиц, называются фазовыми точками. Величина

Г=Г_V∙Г_Р= (3.12)

называется элементом объема фазового пространства.

Г_V = - элемент объема пространства координат;

Г_Р = - элемент объема импульсного пространства

Так как у классической частицы координаты и составляющая импульса могут меняться непрерывно, то элементы Г_v и Г_p, а вместе с ними Г, могут быть сколь угодно малыми.

Для системы невзаимодействующих частиц при отсутствии внешнего поля потенциальная энергия частиц равна нулю. Такие частицы называются свободными. Для свободных частиц удобно пользоваться не шестимерным фазовым пространством, а трехмерным пространством импульсов. В этом случае Г_v равен просто объему, в котором движется частица.

Но если рассматривается квантовый объект (например, электрон), обладающий волновыми свойствами, то деление фазового пространства на элементы объема должно производиться с учетом принципа неопределенности. Т.е. два состояния (x, y, z, p_x, p_y, p_z) и (x + dx, y + dy, z + dz, p_x + dp_x, p_y + dp_y, p_z + dp_z) можно различить, если произведение dxdydzdp_xdp_ydp_z окажется не меньше чем h³. Это произведение выражает элемент объема шестимерного фазового пространства. Поэтому в квантовой статистике за элементарную ячейку шестимерного фазового пространства принимают объем равный

Г= Г_v∙ Г_p = h³ (3.13).

Для свободных микрочастиц, для которых Г_v = V, элемент трехмерного пространства импульса равен

Г_Р = (3.14)

Каждому такому элементу соответствует квантовое состояние, отличное от других состояний. Процесс деления фазового пространства на ячейки конечной величины называют квантованием фазового пространства.

Определим число состояний, которым обладает микрочастица в интервале энергий (E; E+dE), для чего проведем в пространстве импульсов две сферы с радиусами P и P+dP (рис. 3.1).

Между этими сферами находится шаровой слой, имеющий объем равный 4P²dP. Число элементарных фазовых ячеек, заключенных в этом слое

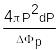= (3.15)

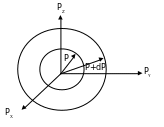
Рисунок 3.1

Так как каждой ячейке соответствует одно состояние микрочастицы, то число состояний, приходящихся на интервал dP, равно

= (3.16)

Для свободных частиц P²=2mE, dE= (P/m)∙ dP, следовательно .

Подставив P и dP в (3.16), получим

= (3.17)

Это и есть число состояний микрочастицы в интервале энергии от E до Е+dE. Поделив (3.17) на dE, получим плотность состояний g(E) , выражающую число состояний частицы, приходящихся на единичный интервал энергий:

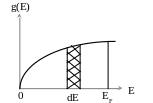
= (3.18)

Рисунок 3.2

Если микрочастицей является электрон, то каждой фазной ячейке отвечает не одно, а два состояния, отличающиеся друг от друга направлением спина. Поэтому для электронов число состояний (3.16 и 3.17) и плотность состояний (3.18) следует удвоить:

= (3.19)

= (3.20)

= (3.21)

Интегрируя (3.17) по энергиям в пределах от 0 до Е, получим число состояний микрочастицы, заключенное в интервале от 0 до Е:

Полагая E = 3/2kT, найдем что

G 

С учетом (3.8) получаем выражение для критерия невырожденности:

, (3.22)

где n=N/V – число частиц в единице объема.

Из (3.22) видно, что невырожденное состояние может быть достигнуто не только повышением температуры, но и уменьшением концентрации n. При n  10²² м ^-3 левая часть уравнения (3.22) для электронов становится  10^-3, что значительно меньше 1, а электронный газ становится невырожденным. Такая и меньшая концентрация электронного газа имеет место в полупроводниках, вследствие чего он становится в них невырожденным и соответственно описывается статистикой Максвелла-Больцмана.