Электрическая проводимость

Электрической проводимостью - называется способность вещества пропускать через себя электрический ток.

Электрическая проводимость (обычно обозначается латинскими буквами G или g) – величина, обратная электрическому сопротивлению. Чем больше сопротивление проводника, тем меньше его проводимость.

Наибольшей проводимостью обладают металлы (серебро, медь, алюминий и др.), их сплавы, растворы кислот, солей и другие проводники электрического тока. Наименьшую проводимость имеют изоляторы (фарфор, резина, слюда, стекло и т.п.) У полупроводников проводимость более высокая, чем у изоляторов, но более низкая, чем у проводников. Величина проводимости полупроводников в широких пределах изменяется под действием света, нагревания, радиоактивности, электрических и магнитных полей, а также от наличия постоянных примесей.

За единицу проводимости принята проводимость проводника с сопротивлением 1 Ом. Измеряется проводимость в СИМЕНСАХ (сим).

Зная сопротивление проводника, легко определить его проводимость, и наоборот. Например, если проводник имеет сопротивление R = 100 Ом, то его проводимость G= 1/1R =1\100= 0,01 сим.

Удельное сопротивление

Электрическое сопротивление проводника зависит от материала, из которого он изготовлен. Эта зависимость учитывается так называемым УДЕЛЬНЫМ СОПРОТИВЛЕНИЕМ ПРОВОДНИКА.- Сопротивлением проводника длиной 1 м. И сечением 1 мм ² .

Измеряется удельное сопротивление Ом мм ² /м.

В таблице 2 приведены примеры удельные сопротивления некоторых материалов.

Таблица № 2.

Материал	Удельное сопротивление Ом мм2 /м.
Серебро	0,016
Медь	0,0175
Алюминий	0,0295
Железо	0,09-0,11
Сталь	0,125-0,146

Расчет сопротивления проводника.

Если увеличивать длину проводника, то число столкновений электронов с атомами и молекулами вещества

будет возрастать, а значит, будет увеличиваться электрическое сопротивление проводника. Мы говорим, что электрическое сопротивление прямо пропорционально длине проводника.

При увеличении поперечного сечения проводника, его сопротивление уменьшается. Это и понятно: с ростом сечения свободным электронам становиться «просторней», число столкновений уменьшается. Таким, образом, электрическое сопротивление обратно пропорционально сечению проводника S.

Математически указанные выше зависимости выражаются формулой

R= * l/S (1)

Где R- сопротивление проводника, Ом.

- удельное сопротивление материала проводника, Ом мм²/м.

l- длина проводника,м;

S- площадь поперечного сечения проводника, мм²;

Напомним, что площадь поперечного сечения круглого проводника

S=πD ²/4;

Где π=3,14

D- диаметр проводника.

Полезно запомнить и следствия из формул для электрического сопротивления,

L=RS/ρ; S=Lρ/1; ρ=RS/E;

Зависимость сопротивления от температуры

С повышением температуры металлических проводников (проводников первого рода) их сопротивление возрастает в среднем на 0,4 % на 1С. С понижением температуры сопротивление на такую же величину уменьшается. Сопротивление проводников второго рода и полупроводников с ростом температуры уменьшается.

При нагревании металлического проводника, возрастает интенсивность хаотического движения атомов вещества, а значит и вероятность столкновения с ними свободных элементов, т.е. увеличивается электрическое сопротивление.

Нерегулируемые и регулируемые резисторы.

В электротехнике и радиоаппаратуре широко применяются нерегулируемые и регулируемые резисторы – детали, обладающие определенным постоянным или регулируемым сопротивлением. К ним относятся, например, реостаты, регулируемые непроволочные и непроволочные резисторы.

Технологическая карта№2.

Изучение последовательного соединения сопротивлений

Цель работы. Научиться собирать электрические цепи по за­данной схеме, подбирать электроизмерительные приборы, измерять напряжения на участках цепи и практически изучить вопрос рас­пределения напряжений в последовательной цепи.

План работы.

1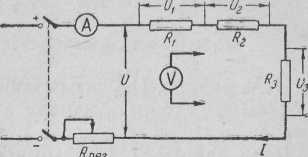 . Ознакомиться с токоприемниками и источни­ком тока на рабочем месте. Записать напряжение источника.

2. Проверить соответствие номинального тока амперметра и на­пряжения вольтметра току и напряжениям, которые будут в цепи.

3. Собрать цепь (рис. 2), сделать необходимые измерения, ре­зультаты записать в таблицу.

4. Сделать необходимые вычисления, сравнить результаты.

Пояснения к работе. Знакомясь с токоприемниками, обратить внимание на допустимые токи в них. Наименьший из них будет до­пустимым током в цепи. По нему проверить реостат и выбрать ре­жим работы цепи. Сопротивление реостата должно быть таким, чтобы допустимый ток в цепи устанавливался при введении не более четвертой части его. Номинальный ток амперметра должен быть не меньше допустимого тока цепи. В то же время амперметр дол­жен измерять и меньшие токи, при которых его показания соответствуют не менее 40% его но­минального тока. Если ампер­метр не удовлетворяет этому ус­ловию, выбрать другой, с двумя пределами измерений.

Рис. 2. Последовательное соединение сопротивлений

Вольтметр предназначен для измерения напряжения на зажи­мах цепи и на участках, поэтому его номинальное напряжение дол­жно быть не меньше, чем источника. В то же время он должен измерять напряжение на участке с наименьшим сопротивлением, при котором показания прибора соответствуют не менее 40% его номинального напряжения. Если вольтметр не удовлетворяет таким условиям, выбрать прибор с двумя пределами измерения. После проверки схемы руководителем, установив реостат на максимальное сопротивление, подключить цепь к источнику тока.

Уменьшая сопротивление реостата, установить в цепи максимально допустимый ток. Измерить напряжение на всех трех токо­приемниках и на отдельных участках. Результаты измерений записать в таблицу 3.

Таблица 3

№ п/п	Измеряются					Вычисляются
	I	U	U1	U2	U3	R1	R2	R3	R	ΣU
	а	в	в	в	в	ом	ом	ом	ом	в

Убедиться в равенстве токов на всех участках цепи.

Повторить опыт еще 1—2 раза при меньших значениях тока. Вычислить величины, указанные в таблице, и найти их среднее значение по результатам нескольких опытов.

Эквивалентное сопротивление цепи R определить по показани­ям приборов. Сделать вывод о соотношениях между напряжениями на отдельных участках. Проверить уравнения:

R = R₁ + R₂ + R₃ и U = U₁ + U₂ + U₃.

При наличии расхождений, объяснить, чем они обусловлены. Про­верить второе правило Кирхгофа. При наличии расхождений объ­яснить их причину.

Дополнительный материал к работе.

Последовательное соединение сопротивлений. Если сопротив­ления соединены между собой так, что конец первого соединен с на­чалом второго, конец второго — с началом третьего и т. д., а ток последовательно проходит через отдельные сопротивления, то та­кое соединение называют последовательным (рис. 3).

Цепь с последовательно соединенными сопротивлениями имеет следующие свойства:

1. Сила тока во всех участках последовательной цепи одна и та же. Это объясняется тем, что цепь не имеет ответвлений и в то же время ни в одном из участков не происходит накопления электро­нов.

2. Падения напряжения на отдельных участках цепи пропорцио­нальны сопротивлениям этих участков.

Действительно, согласно закону Ома, U₁=IR₁; U₂=IR₂; U₃ ==IR₃ и т. д. Следовательно:

и аналогично:

3. Напряжение на зажимах последовательной цепи равно сумме напряжений на отдельных ее участках, то есть U = U₁+U₂+U₃

Это свойство следует из определения понятия о напряжении ме­жду двумя точками электрического поля и между двумя точками электрической цепи, согласно которому напряжение на зажимах последовательной цепи измеряется работой, совершенной при пере­мещении единицы заряда по этой цепи и состоящей из суммы работ на отдельных участках.

4. Эквивалентное сопротивление последовательной цепи равно сумме сопротивлений отдельных ее участков, то есть R = R₁+R₂ +R₃

На основании закона Ома (см. вывод второго свойства) и ра­венства:

U = U₁+U₂+U₃

имеем:

IR = IR₁ + IR₂ + IR₃.

или, сокращая уравнение на I, получим:

R= R1+R₂+R₃.

Пример . Определить напряжение на концах цепи, изображенной на рисун­ке 3, и напряжения на участках, если R₁=6 ом, R₂=4 ом, R₃=2 ом и падение напряжения на третьем участке U₃₌20 в.

Решение. Согласно закону Ома, ток в третьем участка

I₃=

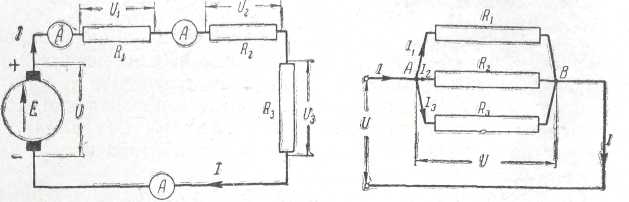
Рис. 3. Схема последовательной цепи Рис. 4. Схема параллельной цепи

Технологическая карта№3

Изучение параллельного соединения сопротивлений

Цель работы. Научиться собирать электрические цепи по задан­ной схеме, подбирать измерительные приборы и практически изу­чить распределение токов в параллельных ветвях.

План работы.

1.Ознакомиться с токоприемниками и источни­ком тока. Записать напряжение источника.

2. Проверить соответствие измерительных приборов режимам, которые будут в цепи.

3.Собрать цепь (рис.5), сделать необходимые измерения, ре­зультаты записать в таблицу 4.

4. Провести вычисления, сравнить результаты и сделать вы­воды.

Таблица 4

№ п/п	Измеряются					Вычисляются
	U	I1	I2	I3	I	R1	R2	R3	g	∑I
	в	а	а	а	а	ом	ом	ом	сим	а

Пояснения к работе. Оценив сопротивления токоприемников и зная напряжения источника тока, определить ориентировочно значение тока в каждом токоприемнике. Если он не превосходит допустимой для данного токоприемника величины, выбрать ампер­метр с таким расчетом, чтобы найденный ток составлял 80—90% номинального тока амперметра. Если же найденный ток превосхо­дит допустимый, то амперметр подбирать по току, допустимому для данного участка. Так же подобрать амперметры для других участков.

Амперметр в неразветвленном участке и реостат подобрать по сумме токов в участках. Сопротивление реостата выбрать, как и в предыдущих работах.

После сборки цепи и провер­ки ее руководителем ввести рео­стат полностью и подключить цепь к источнику тока. Сопро­тивление реостата уменьшать до тех пор, пока ток в одном из то­коприемников не достигнет мак­симально допустимой величины или реостат не окажется полностью выведенным.

.

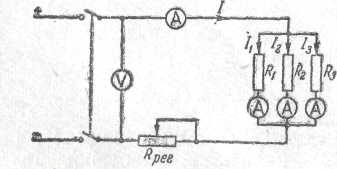
Рис. 5. Параллельное соединение сопротивлений.

Показания приборов, соответствующие этому положению движка реостата, записать в таблицу4. Эти измере­ния повторить дважды при меньших значениях тока.

По результатам измерений подсчитать сопротивления токопри­емников, проводимость всей цепи (по показаниям приборов), сум­му токов в участках и их средние значения по результатам прове­денных опытов. Сделать вывод, в каком сопротивлении течет наи­больший ток. Проверить уравнения I= I₁ + I₂ + I₃; g = , При наличии расхождений объяснить их причины.

Дополнительный материал к работе.

Параллельное соединение сопротивлений. Параллель­ным называют такое соединение, при котором начала всех сопро­тивлений соединены в одной точке, концы — в другой, а ток раз­ветвляется по отдельным сопротивлениям (рис.5). Параллельная цепь обладает следующими свойствами.

1. Напряжение на параллельно соединенных участках одно и то же, то есть U₁ = U₂ = U₃=U, так как все параллельно соединенные участки подсоединены к одним и тем же зажимам А и В, напряже­ние между которыми и является напряжением на отдельных участках.

2. Сумма токов отдельных ветвей равна току до разветвления, то есть I = I₁ + I₂ + I₃- Это свойство объясняется тем, что электроны в узловой точке накапливаться не могут.

3. Токи в параллельных ветвях обратно пропорциональны, вели­чинам сопротивлений этих ветвей.

На основании закона Ома, для первого участка:

I₁ =

Аналогично для второго и третьего участков:

I₂ = и I₃ =

Отсюда, разделив первое уравнение на второе, а второе на третье, получим:

после сокращения правых частей уравнений на U

4. Эквивалентная проводимость параллельной цепи равна сумме проводимостей отдельных параллельных ветвей.

Действительно, согласно закону Ома для участка цепи и на ос­новании второго свойства,

После сокращения обеих частей уравнения на U

или

g = g₁ + g_{2 +} g₃,

где g—эквивалентная проводимость параллельной цепи;

R — эквивалентное сопротивление параллельной цепи.

Если параллельно соединены два сопротивления, то

Откуда

R=

Таким образом, эквивалентное сопротивление параллельной це­пи подсчитывают через проводимость, и лишь в случае параллель­ного соединения двух сопротивлений можно воспользоваться пос­ледней формулой.

Смешанное соединение соп­ротивлений. Смешанным называется такое соединение, при котором часть сопротив­лений, входящих в цепь, сое­динена последовательно, а часть — параллельно.

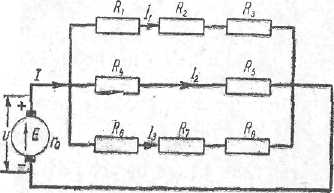
Рис. 6. Схема цепи со смешанным соединением сопротивлений.

Видов смешанных соединений мо­жет быть очень много. На рисунке 6 изображена сме­шанная цепь, которая представляет собой три последовательных участка, соединенных парал­лельно.

Конкретного способа решения смешанных цепей указать нельзя из-за их большого разнообразия, но в общем случае сначала е следует решить последовательно соединенные участки, а потом — па­раллельные или наоборот.

Напряжение на зажимах внешнего участка U=IR=4·4=16в

Ток в верхней ветви

I₁=

Ток в средней ветви

I₂=

Ток в нижней ветви

I₃=

Падение напряжения внутри генератора U₀=E—U=24—16=8 В.

Технологическая карта№4

Измерение работы и мощности в цепи постоянного тока.

Цель работы – ознакомиться с методами измерения работы и мощности в цепи постоянного тока и научиться для этой цели правильно включать в цепь электроизмерительные приборы.

Пояснение. Если ламповый реостат с сопротивлением R находиться под напряжением U, и по нему проходит ток, то за время t в нем выделяется энергия, которую можно подсчитать по формуле:

W=IUt=U² t\ R=I² R t

Мощность – это работа (энергия ) совершенная в единицу времени

P = W / t.= I * U

Измеряют мощность ваттметром. Для измерения мощности постоянного тока достаточно вольтметра и амперметра. Для измерения работы электрического тока применяют счетчик электрической энергии. Счетчики измеряют работу в киловатт – часах.

Работу электрического тока можно определить, измеряя мощность вольтметром и амперметром, а время секундомером.

Оборудование и аппаратура.

амперметр постоянного тока на 3А	1шт.
Вольтметр постоянного тока на 150 В.	1 шт.
Патроны с лампочками накаливания 110 В, 100Вт.	3 шт.
Провода соединительные площадью сечения 1,5 мм2 длиной 1,5 м	9шт.
Рубильник двухполюсный на 25 А, 250В	1шт.
Источник постоянного тока напряжением 115 В.

Порядок выполнения работы.

1.Ознакомиться со схемой измерения и приборами.

2.Собрать схему (рис 7 а), подключить ее к сети, и записать показания приборов в таблицу.

3. Вычислить мощность и энергию ( работу )

4. Собрать схему ( рис 7 б ), включить ее в сеть и записать показания в

таблицу .

5. Вычислить мощность и энергию.

6.Составить отчет.

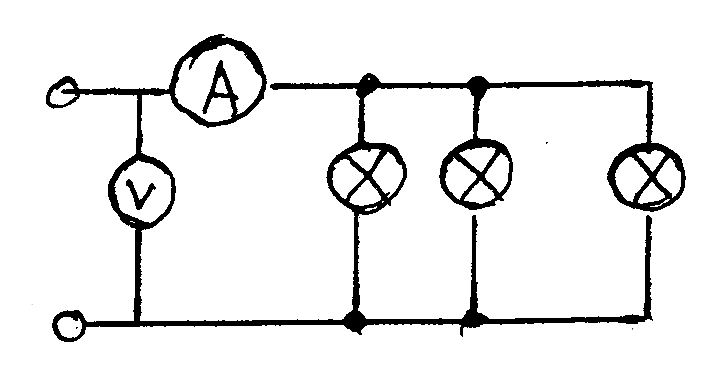
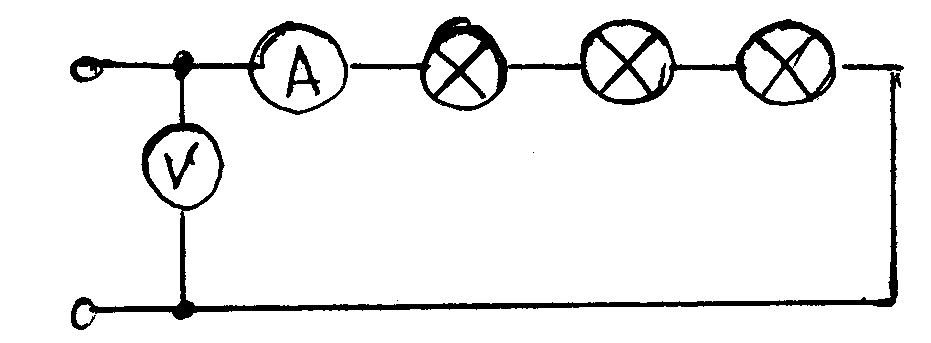
а б

Рис7. Измерение мощности в цепи постоянного тока при включении потребителей:

а – последовательно б - параллельно

соединенение	измерено		вычислено
	I. А.	U. В.	R. Ом	P. Вт.	t. с	W. дж.
Последователь- ное
Параллельное

Содержание отчета.

1. Наименование отчета.

2. параметры электроизмерительных приборов.

3. Электрические схемы измерения работы и мощности.

4. Таблица с измеренными и вычисленными величинами.

5. Формула для вычисления работы и мощности в цепи постоянного тока.

Контрольные вопросы.

1. Что такое работа и мощность в электрической цепи, и в каких единицах их измеряют?

2. Какими приборами измеряют мощность постоянного тока?

3. Какими приборами, и в каких единицах измеряют электрическую энергию?

Дополнительный материал к работе.

Энергия и мощность электрического тока.

Проходя по цепи, электрический ток совершает работу. Способность электрического тока совершать работу называется энергией электрического тока.

Энергия расходуется электрическим током в цепи, численно равна количеству электричества, проходящему по цепи, умноженному на подведенное к цепи напряжение. Энергия обозначается буквой W.

Зная, что количество электричества Q=It, можно написать выражение для энергии.

W=Р*U = U*I*t

Таким образом, энергия электрического тока численно равна произведению напряжения на величину тока и на время, в течении которого он проходит.

За единицу электрической энергии принято Ватт- секунда (Вт*сек). Энергия, которая сообщается электрической цепи током 1А при напряжении 1В в течение 1 сек, равна одной Ватт – секунде.

1 гектоватт* час (квт-ч)=100 вт*ч=360 000 вт. Сек.

1 киловатт* час (квт-ч)=1000вт*ч

Приборы для измерения электрической энергии называется счетчиками

В электротехнике, кроме того, введено понятие о мощности электрического тока. Это необходимо для того, чтобы характеризовать способность источника электрической энергии отдавать в цепь то или иное количество энергии в единицу времени.

Поэтому МОЩНОСТЬЮ электрического тока называют энергию тока, отнесенного к единице времени.

Обозначается она латинской буквой Р:

Р= W / t

Подставляя вместо энергии W ее значение из предыдущей формулы, получим:

Р=U I t / t

Или: Р=U I

Мощность электрического тока численно равна произведению величины тока на величину напряжения. За единицу мощности принят Ватт.

Ватт – это мощность электрического тока величиной 1А при напряжении 1В.

1КВТ=1000 Вт

встречается и еще более крупная единица мощности – мега ватт.

1 МВТ= 1 000 000 Вт.

Из основной формулы для определения мощности тока P=UI легко получить ее разновидности. Так как U=I R, то P=I R*I или P= I² R;

Т.е. мощность электрического тока равна произведению квадрата величины тока на сопротивление.

Заменив в основной формуле мощности I=U / R, получим Р = U² / R, т.е. мощность электрического тока равна квадрату напряжения, деленному на сопротивление.

Для измерения мощности электрического тока применяется прибор, называемый Ваттметром.

Контрольное задание.

Для предыдущих задач определить мощность электрического тока и энергию за 10 часов.

Технологическая карта№5.

Последовательное, параллельное и смешанное соединение аккумуляторов.

Цель работы – ознакомиться с различными типами аккумуляторов; научиться составлять батареи аккумуляторов.

Оборудование и аппаратура

Амперметр постоянного тока на 10 А. ………………….. 1 шт.

Амперметр постоянного тока на 3 А ……………………. 3 шт.

Вольтметр постоянного тока на 15 В. ………………….. 2 шт.

Аккумуляторы …………………………………………… 15 шт.

Реостат проволочный на 10 А, 2,5 Ом …………………. 1 шт.

Провода соединительные площадью сечения

2,5 мм², длиной 1,5 м. …………………………………… 15 шт.

Рубильник однополюсный на 25 А. ……………………. 1 шт.

Порядок выполнения работы

1. Ознакомиться со схемой измерения.

2. Собрать схему (см. рис. 8, а) и записать показания приборов в таблицу при включенной нагрузке.

соединение

измерено

вычислено

С нагрузочным сопротивлением

Без нагрузочного сопротивления

U1, В

U2, В

U3,В

Uн,, В

I1, А

I2, А

I3, А

Iн, А

Е1, В

Е2, В

Е3, В

I1, А

I2, А

I3, А

r1, Ом

r0, Ом

паралельное

последовательное

смешанное

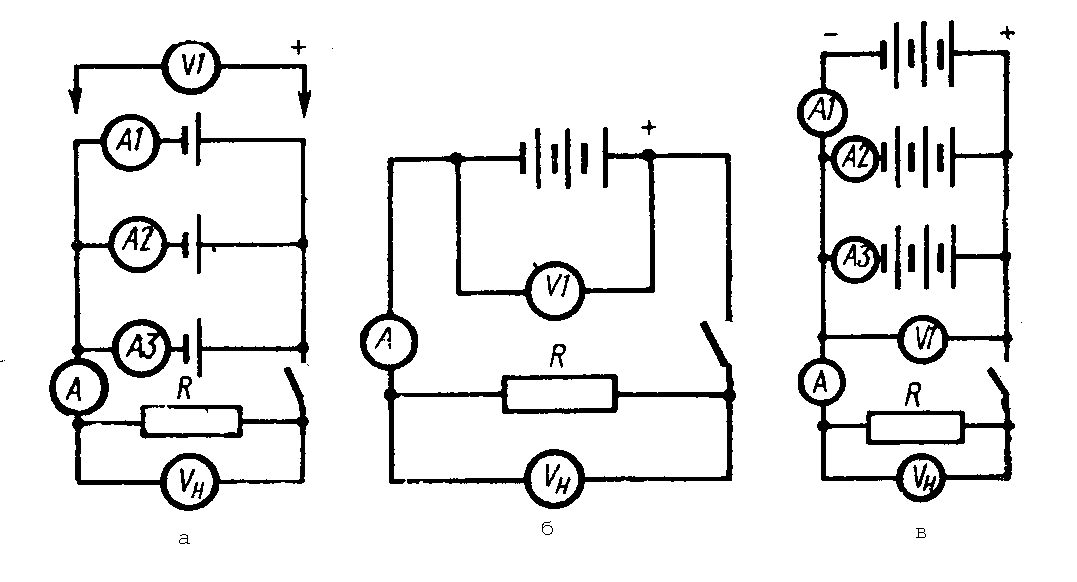
Рис.8 . Соединение аккумуляторов

а – параллельное, б – последовательное, в – смешанное; V₁ – вольтметр для измерения э.д.с. и напряжения на аккумуляторе. V_{н – вольтметр для измерения напряжения на сопротивлении нагрузки.}

3. Отключить нагрузочный реостат и записать значение э. д. с. батареи и силу тока каждого аккумулятора.

4. Подсчитать по формуле внутреннее сопротивление аккумуляторной батареи r и каждого аккумулятора ro при параллельном соединении

;

5. Собрать схему (рис 8, б) и записать показания приборов в таблицу при включённой нагрузке.

6. Отключить нагрузочный реостат и записать значение э.д.с. батареи и каждого аккумулятора.

7. Подсчитать внутреннее сопротивление батареи и каждого аккумулятора при последовательном соединении

; .

8. Собрать схему и записать показания приборов при включённой нагрузке.

9. Отключить нагрузочный реостат и записать показания приборов.

10. Подсчитать внутреннее сопротивление всей батареи при смешанном соединении аккумуляторов.

11. Составить отчёт.

Примечание: При отсутствии аккумуляторов, можно использовать гальванические элементы. В этом случае нужно подобрать приборы, соответствующие напряжению ёмкости гальванических элементов, а вместо проволочного реостата подобрать переменный резистор.

Содержание отчёта:

1. Наименование отчёта.

2. Параметры электроизмерительных приборов и оборудования.

3. Электрические схемы включения аккумуляторов.

4. Таблица с измеренными и вычисленными величинами.

5. Формулы для расчёта э. д. с. батареи аккумуляторов при последовательном, параллельном и смешанном соединениях.

6. Формулы для расчёта внутреннего сопротивления аккумулятора.

7. Формулы для расчёта внутреннего сопротивления батареи аккумуляторов при последовательном, параллельном и смешанном соединениях.

Контрольные вопросы:

1. Что такое аккумулятор, и какие типы аккумуляторов вы знаете?

2. Чему равна э.д.с. аккумулятора?

3. Как определить ёмкость аккумулятора, и в каких единицах её измеряют?

4. На какую величину отличается напряжение на аккумуляторе от его э.д.с.

Дополнительный материал к работе.

Пояснения. Аккумулятор является химическим источником тока и для того, чтобы он отдавал ток, его необходимо предварительно зарядить. Вследствие электрохимического процесса в аккумуляторе возникает электродвижущая сила (э. д. с.). Если к аккумулятору присоединить нагрузочный реостат, в цепи возникает сила тока, равная по закону Ома для электрической цепи с э. д. с.

Где R – сопротивление реостата нагрузки, Ом; ro – внутреннее сопротивление одного аккумулятора, Ом; Е – э. д. с. Аккумулятора, В.

Рис.8 . Соединение аккумуляторов

а – параллельное, б – последовательное, в – смешанное; V₁ – вольтметр для измерения э.д.с. и напряжения на аккумуляторе. V_{н – вольтметр для измерения напряжения на сопротивлении нагрузки.}

Напряжение на сопротивлении реостата нагрузки

U=IR

меньше э. д. с. Аккумулятора на величину Iro, называемую внутренним падением напряжения в аккумуляторе. Таким образом, напряжение на зажимах аккумулятора

U = E - Ir₀

Ёмкость аккумулятора Q равна произведению разрядного тока на время разряда и определяется в ампер-часах.

Если в цепи нагрузки хотят получить большую силу тока (большую, чем разрядный ток одного аккумулятора), аккумуляторы соединяют параллельно (рис. 8, а), а если нужно получить большее напряжение (большее, чем напряжение одного аккумулятора), их соединяют последовательно (рис. 8, б). Когда необходимо увеличить и силу тока и напряжение, используют смешанное соединение (рис.8, в).

При параллельном соединении аккумуляторов с одинаковыми э. д. с., э. д. с. всей батареи равна э. д. с. одного аккумулятора

Е = Е₁ = Е₂ = Е₃ = … Е_n

Внутреннее сопротивление батареи аккумуляторов, состоящей из m одинаковых аккумуляторных блоков, соединённых параллельно.

При последовательном соединении n одинаковых аккумуляторов э. д. с. батареи равна сумме э.д.с. всех аккумуляторов

Е = Е₁ + Е₂ + Е₃ + …. + Е_n = nЕ₁

а внутреннее сопротивление такой батареи из n одинаковых элементов равно сумме внутренних сопротивлений этих аккумуляторов r = r₀₁ + r₀₂ + … +r_0n = nr₀

При смешанном соединении одинаковых аккумуляторов э. д. с. всей

батареи E = nE₁,

а внутреннее сопротивление батареи .

Технологическая карта№6

Исследование неразветвленной цепи переменного тока

Цель работы. Научиться измерять ток и напряжение в цепях переменного тока. Практически изучить явления, наблюдающиеся в последовательных цепях переменного тока.

Внимание: Во избежание поражения электрическим током и повреждения приборов рекомендуется схему включать через понижающий трансформатор

План работы.

1. Ознакомиться с работой и оборудованием на рабочем месте.

2. Выбрать амперметр по режиму резонанса напряжений.

3. Собрать цепь (рис. 9) и после проверки ее мастером подключить к источнику тока.

4. Измерить токи и напряжения при различных положениях рубильников P₁ и Р₂. Результаты измерений записать в таблицу.

5. Сделать необходимые вычисления и сравнить результаты.

6. Изменяя величину индуктивности или емкости, добиться ре­зонанса напряжений.

7. Измерить ток в цепи и напряжение на участке в режиме ре­зонанса напряжений.

8. Сравнить результаты и сделать выводы.

Пояснение к работе. Приступая к работе, обратить внимание на соотношения между напряжением сети и напряжениями на от­дельных участках цепи в режиме резонанса, на конструкцию и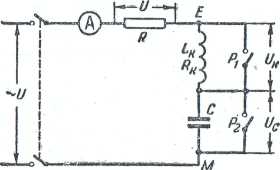 н­дуктивности и емкости и

Рис. 9. к практической работе 6.

выяснить, каким путем можно изменять их величину. Так как в режиме резонанса напряжений ток достига­ет наибольшей величины, то амперметр нужно выбирать исходя из этого режима; Оценив величину активного сопротивления, подсчи­тать приближенно значение тока в режиме резонанса напряжений.

При выполнении работы прове­сти три цикла измерений:

1) цепь содержит одно актив­ное сопротивление;

2) цепь содержит активное соп­ротивление и индуктивность;

3) в цепь включены все три сопротивления.

С помощью моста для измерения сопротивлений или иным способом определить активное сопротивление R_K индуктивности. Замкнув рубильники Р₁ и Р₂ получить цепь с активным сопротив­лением. Измерив ток и напряжение, вычислить величину этого со­противления .

Разомкнув рубильник Р₁, получить цепь с активным сопротив­лением и индуктивностью. Измерив, ток и напряжение всей цепи, подсчитать полное сопротивление катушки, причем под активным сопротивлением цепи следует подразумевать сумму активного сопротивления R и активного со­противления катушки R_K. Кроме того, вычислить активную мощ­ность Р₂ и коэффициент мощности cos φ₂. Результаты измерений и вычислений записать в таблицу .

№ измерения	Измеряются		Вычисляются
	I2	U2	z2	ХL	соs φ2	Р2
	а	в	ом	ом	-	вт

Разомкнув и второй рубильник, получить последовательную цепь с активным сопротивлением, индуктивностью и емкостью.

Обратить внимание на ток в цепи. Как он изменился после вве­дения в цепь еще одного сопротивления? Записав новые значения тока и напряжения, определить полное сопротивление цепи в этом случае z₃, результирующее реактивное сопротивление, величину емкостного сопротивления, cos φ_з и величину активной мощности Р₃. Результаты измерений и вычислений записать в таблицу .

№ измерения

Измеряются

Вычисляются

Iрез

I3

U3

Uк

UС

UЕМ

z3

Х

ХС

соsφ3

Р3

ХL

а

а

в

в

в

в

ом

ом

ом

-

вт

ом

Подсчитанное значение Х_с окажется либо больше, либо мень­ше X_L. В зависимости от этого решить вопрос, что нужно сделать для получения в цепи режима резонанса напряжений? Добиться его.

Записать значение тока цепи в этом случае, напряжение U_EM, напряжения на индуктивном и емкостном сопротивлениях. Вычис­лить величины, указанные в таблице 11, и занести их туда. Срав­нить ток I₂ с током I₃. Почему I₂<I₃, хотя в последнем случае в цепь добавлено еще одно сопротивление? Чем объяснить, что cos φ₃ >cos _φ2? Почему Р₃>Р_2. Почему в режиме резонанса напря­жение U_EM≈0, a X_L≈X_C?

Чем объяснить, что в режиме резонанса напряжений ток I_рез больше токов в иных режимах, a cos φ_рез≈1?

Можно ли компенсировать сдвиг фаз, созданный индуктивной нагрузкой, включением последовательно с ней емкости соответст­вующей величины?

Дополнительный материал к работе.

Последовательная цепь с активным, индуктивным и емкостным сопротивлениями

Векторная диаграмма и сдвиг фаз. Для того чтобы выяснить явления, происходящие в такой цепи (рис, 10,а), необходимо по­строить ее векторную диаграмму.

Допустим, что X_L>X_C. Задавшись масштабом тока и отложив вектор последнего, построим вектор общего напряжения U путем геометрического сложения напряжений на отдельных участках це­пи (рис. 10,6). Напряжение на активном сопротивлении всегда совпадает по фазе с током, текущим через него, поэтому, задав­шись масштабом напряжений, откладываем вектор U_a в направле­нии вектора тока. Напряжение на индуктивном сопротивлении опережает ток в нем па 90°, поэтому вектор U_L пристраиваем к концу вектора активного напряжения, направив его вверх перпендикулярно вектору тока. Вектор напряжения U_c пристраиваем к концу вектора U_L, направив его вниз перпендикулярно вектору тока, так как напряжение на зажимах емкости отстает от тока в ней на 90°. Замыкающая, проведенная из начала первого вектора до конца по­следнего (ОВ), представляет собой сумму этих трех векторов, то есть напряжение на зажимах цепи.

Из векторной диаграммы видно, что напряжение опережает ток на угол φ, причем угол φ получился меньше того, который был бы в цепи при отсутствии в ней емкости (пунктир ОА).

Т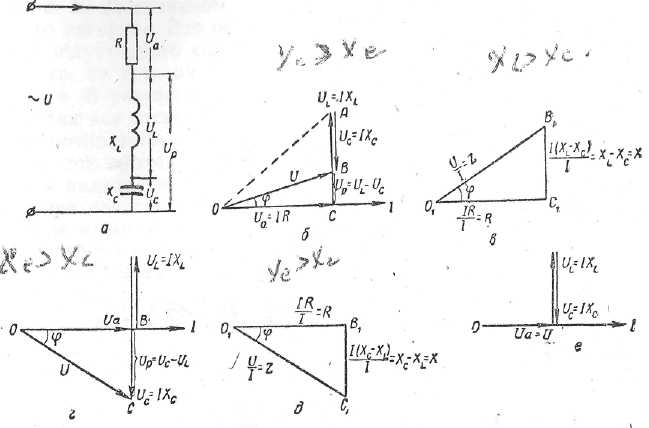 реугольник ОВС - является треугольником напряжений этой цепи. При рассмотрении его видно, что напряжения находятся в таких же соотношениях, как и в предыдущих случаях, но реактив­ная составляющая U_р, в свою очередь, состоит из двух составляю­щих U_L и U_С.

Рис. 10. Общий случай последовательной цепи:

а — схема цепи: б, г и е — векторные диаграммы; в и д—треугольники сопротивлений.

Из векторной диаграммы U_P=U_L- U_C = IX_L—IX_С = I(X_L—Х_С).

Разделив все стороны треугольника напряжений на величину силы тока, получим треугольник сопротивлений О₁ В₁ С₁ (рис. 10, в).

Из треугольника сопротивлений следует, что результирующее реактивное сопротивление цепи X равно разности индуктивного и емкостного сопротивлений. Емкостное сопротивление как бы ча­стично уничтожает индуктивное, а полное сопротивление цепи z =

Математическое выражение закона Ома для этого случая остается таким же, как и для предыдущего случая,

I =

Таким образом, анализируя векторную диаграмму и отдельно треугольники напряжений и сопротивлений, мы можем заключить, что когда в последовательной цепи преобладает индуктивное со­противление, то есть X_L>X_C, то она ведет себя в целом, как цепь индуктивная. Например, если активное сопротивление цепи 20 ом, индуктивное 80 ом и емкостное 30 ом, то цепь можно считать состоящей из активного сопротивления 20 ом и индуктивного 50 ом.

Вычисления активной, реактивной и полной мощностей, актив­ного и реактивного токов, активной и реактивной проводимостей можно проводить так же, как для любой индуктивной цепи,

Если в цепи преобладает емкостное сопротивление (X_C>X_L_), то на векторной диаграмме вектор U_C больше вектора U_L; а ре­зультирующее реактивное напряжение U_p равно разности емкост­ного и индуктивного напряжений (рис.10,г). В этом случае ток опережает напряжение на некоторый угол φ, и цепь ведет себя как цепь емкостная.

Треугольник сопротивлений можно получить как обычно, раз­делив все стороны треугольника напряжений на величину силы то­ка I (рис. 10. д).

Пример. Последовательно с катушкой, обладающей активным сопротивлением 24 ом и индуктивностью 0,07 гн, включен конденсатор емкостью 79,6 мкф. Определить характер нагрузки, напряжение на ее зажимах, активную мощность и сдвиг фаз, создаваемый этой нагрузкой, если сила тока в катушке 7 а.

Решение. X_L=2πfL=2 · 3,14 · 50,0 · 0,07=22 ом;

Хс=

Так как X_C>X_L, то нагрузка имеет емкостный характер и ток в ней опережает напряжение на некоторый угол φ.

z =

Напряжение на зажимах цепи U =Iz= 7 · 30 =210в

Коэффициент мощности

cos φ = ; <φ = 36⁰45

Активная мощность цепи

Р = UI cos φ = 210·7·0,8= 1176 вт.

Резонанс напряжений. Особый интерес представляют явления, которые наблюдаются в последовательной цепи при равенстве ин­дуктивного и емкостного сопротивлений (рис.10,е). Из векторной диаграммы видно, что при равенстве индуктивного сопротивлений напряжение на зажимах всей цепи (U) равно на­пряжению на ее активном сопротивлении (U_а) и цепь ведет себя как чисто активная. Это объясняется тем, что при Х_L = Х_С влияние на цепь индуктивного сопротивления скомпенсировано влиянием емкостного, то есть они как бы полностью взаимно уничтожают друг друга. В результате этого ток в цепи становится максималь­ным, но так как отсутствует лишь влияние индуктивного и емкост­ного сопротивлений, а сами они в цепи имеются, то этот макси­мальный ток проходит и через них, вызывая как в одном, так и в другом падение напряжения (U_L и U_С).

Явление совпадения по величине падения напряжений на ин­дуктивном и емкостном сопротивлениях в последовательной цепи переменного тока называется резонансом напряжений. В режиме резонанса напряжений

z =

Ток в цепи максимален, так как знаменатель в этом случае минимален. При этом < φ = 0, а соs φ=1.

Таким образом, в режиме резонанса напряжений явления в це­пи протекают так, как будто в ней осталось лишь одно активное сопротивление.

То обстоятельство, что при последовательном подключении ем­кости угол сдвига фаз, созданный индуктивностью, уменьшается (пунктир ОА на рисунке 10,6),, а при X_C = X_L становится равным нулю, не удается использовать в потребительских установках для уменьшения сдвига фаз, созданного индуктивными токоприемника­ми, так как подключение конденсатора последовательно с токопри­емником сопровождается увеличением тока. Если считать, что до подключения конденсатора ток был номинальным, то после под­ключения он станет больше номинального, что для токоприемника недопустимо, хотя он и будет работать с большим cos φ. Более то­го, в силовых цепях резонанс напряжений — явление опасное. Так при малом активном сопротивлении цепи ток может достигнуть очень большой величины, на которую установка не рассчитана и кроме того, если индуктивное и емкостное сопротивления велики, этот ток вызовет на их зажимах очень большие напряжения (пере­напряжения), в десятки и сотни раз превышающие нормальное ра­бочее, что может привести к пробою диэлектрика емкости и изоля­ции индуктивности.

Пример. В цепь последовательно включены катушка с активным сопротив­лением 10 ом и индуктивностью 300 мгн и конденсатор емкостью 33,8 мкф. Оп­ределить ток в цепи и напряжение на каждом сопротивлении (рис. 10, а). Решение. Индуктивное сопротивление катушки

Х_L=2πfL=314·0,3=94,2 ом

Емкостное сопротивление конденсатора Х_С = ом

Х_L = Х_С , следовательно, в цепи имеется резонанс напряжений и

z = ом

Ток в цепи I =

Напряжение на реактивных сопротивлениях

U_L =U_С= IX_L = 22·94,2=2070в; U_а= IR = 22·10=220в

Напряжение на реактивных сопротивлениях больше напряжения сети почти в 10 раз.

Ток до подключения емкости I=

Следовательно, после подключения емкости он возрос почти в 14 раз.

В радиотехнике это явление используется весьма широко, по­зволяя вследствие образования на зажимах индуктивности и ем­кости значительных напряжений получить усиление очень слабых радиосигналов.

Для того чтобы специально создать равенство индуктивного и емкостного сопротивлений, необходимо либо Х_С подогнать под X_L (подобрав конденсатор соответствующей емкости), либо Х_L по­догнать под Х_С (подобрав катушку соответствующей индуктивно­сти).

Так как индуктивное сопротивление катушки и емкостное со­противление конденсатора зависят от частоты, причем при измене­нии последней они изменяются взаимообратно (если с увеличением частоты Х_L увеличивается, то Х_С — уменьшается, и наоборот), то даже при любой катушке и любом конденсаторе в цепи можно до­биться резонанса напряжений, подобрав частоту, при которой X_L этой катушки окажется равным Х_С конденсатора.

Эту частоту обычно называют резонансной и обозначают fрез. Ее можно определить, имея в виду, что при этой частоте X_L = X_C или 2πf_peзL = , откуда 4π²f²_резLС=1, или f²_рез =

Окончательно f_рез =

В этой формуле L измеряется в генри, С – в фарадах, f_рез – в герцах.

Пример Определить резонансную частоту для цепи, изображенной на ри­сунке 10а, если индуктивность катушки 4 гн, а емкость конденсатора 1 мкф. Решение.

f_рез =

Это значит, что, если к цепи подвести переменное напряжение с частотой 79,6 гц, емкостное сопротивление конденсатора окажется равным индуктивному сопротивлению катушки.

Технологическая карта№7

Исследование разветвленной цепи переменного тока

Цель работы. Научиться измерять ток, напряжение и мощ­ность в цепях переменного тока. Практически изучить явления в параллельной цепи, содержащей индуктивность и емкость.

План работы.

1. Ознакомиться с работой и оборудованием на рабочем месте, записать или измерить величину активного сопро­тивления катушки.

2. Собрать цепь (рис. 11) и после проверки руководителем под­ключить ее к источнику тока.

3. Измерить ток, напряжение и мощность при разомкнутом и замкнутом рубильнике Р.

4. Выполнить необходимые вычисления, сравнить результаты и сделать выводы.

5. Меняя величину индуктивности или емкости, добиться резо­нанса токов.

6. Измерить токи и напряже­ния в режиме резонанса токов.

7. Сравнить результаты изме­рений и сделать выводы.

Пояснения к работе. При вы­полнении этой работы проделать три цикла измерений:

1) при отключенной емко­сти С;

2) при подключенной емкости;

3) в режиме резонанса токов.

Р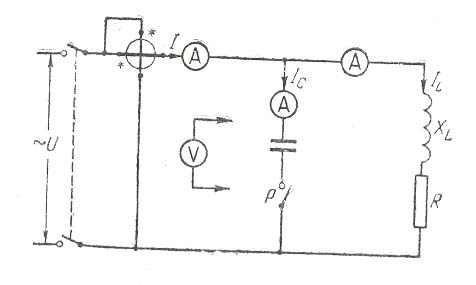 ис. 11. К практической работе 7

При разомкнутом рубильнике Р цепь содержит индуктивное и активное сопротивления (на рисунке 11 активное сопротивление катушки изображено вынесенным из нее). Измерив, напряжение на зажимах цепи, ток в ней и ее активную мощность, подсчитать пол­ную мощность цепи S, ее полное сопротивление z, соs φ, активную и реактивную составляющие тока, используя соотношения из тре­угольников сопротивлений, тока и мощностей. Результаты измере­ний и вычислений записать в таблицу.

№ изме­рения	Измеряются					Вычисляются
	U	I	IC	IL	Р	S	cos φ	z	Iа	Iр
	в	а	а	а	вт	ва	-	ом	а	а

В этой таблице I_с — ток в емкостной ветви; I_L — ток в индуктивной ветви.

При замкнутом рубильнике Р получается параллельная цепь с индуктивностью и емкостью. В этой цепи, кроме величин, измеря­емых в предыдущем случае, определить токи в емкостной и индук­тивной ветвях. Результаты измерений и вычислений записать в ту же таблицу.

Чтобы получить в цепи резонанс, изменяя величину емкости или индуктивности, добиться минимального показания амперметра, включенного до разветвления, так как при резонансе токов общий ток цепи состоит только из активной составляющей.

Показания всех приборов, отмеченные при резонансе, записать в ту же таблицу.

Сравнить между собой токи в неразветвленном участке цепи I до подключения и после подключения емкости. Чем объяснить, что после подключения емкости ток в неразветвленном участке цепи уменьшился, а ток индуктивной ветви I_L остался прежним?

Подсчитать разность между реактивными токами цепи в пер­вом и во втором опыте и сравнить ее с током емкостной ветви I_с. Чем объяснить, что они приблизительно равны?

Почему после подключения емкости показания ваттметра не изменились?

Дополнительный материал к работе.

Резонанс токов.

Сущность явления и векторные диаграммы. Если параллельно индуктивному токоприемнику (он может представлять собой эк­вивалент ряда индуктивных токоприемников) подключить конден­сатор (рис. 12, а), то угол сдвига фаз между током цепи и прило­женным напряжением можно определить через его тангенс. Из треугольника проводимостей (рис. 12 , г).

tg φ =

В данном примере в = в_L—в_с,

где в_L — реактивная проводимость индуктивной ветви;

в_с — реактивная проводимость емкостной ветви.

Следовательно, в данном примере tgφ =

Если в цепи в_L>в_c, то tgφ получится положительным, следова­тельно, и угол φ будет положительным. Это означает, что цепь но­сит индуктивный характер (рис. 78,6). На диаграмме вектор тока I_Р2 короче вектора I_р1 , так как в_L>в_с. Поэтому ток I отстает от напряжения на угол φ.

Если в цепи в_c>в_L, то tgφ отрицательный, то есть цепь носит емкостный характер (рис. 12, в). На диаграмме вектор тока I_р2 длинней, чем I_р1 , так как в_с>в_L. Поэтому ток I опережает напря­жение на угол φ.

Как видно из этих диаграмм, величина и знак угла φ зависят от соотношения между реактивными проводимостями ветвей в_L и в_с-

Если в_L = в_с то tgφ =

Следовательно, <φ = 0, значит цепь ведет себя, как активная (Рис. 12, г).

При этом реактивная составляющая тока Iр=Uв=U0 = 0. Пол­ный ток в цепи I= По величине он минимален, так как в нем полностью отсутствует реактивная составляющая и он равен своей активной составляю­щей. Несмотря на то, что от ге­нератора течет ток, не содержа­щий реактивной составляющей, реактивные токи в ветвях есть (I_Р1=U_ВL И I_Р2 = Uвс).

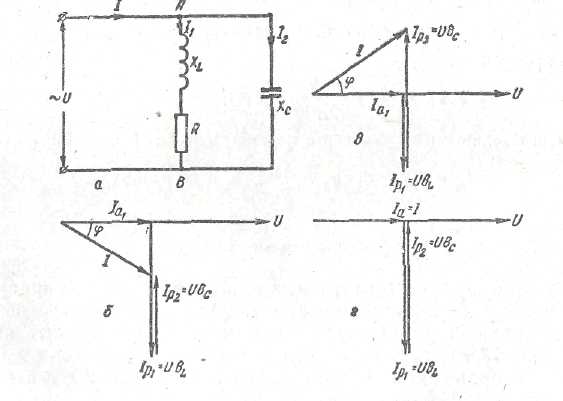
Рис. 12. Резонанс токов:

а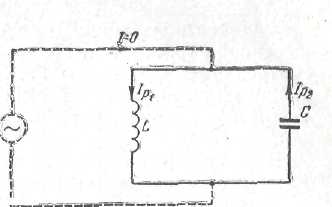 — схема цепи; б, в и г — векторные диаграммы.

Рис. 13. Колебательный контур в це­пи с переменной э. д. с.

Это обстоятельство объясня­ется тем, что реактивные токи в индуктивности и емкости по фазе не совпадают друг с другом на 180°, они всегда противоположны друг другу, и если в индуктив­ности в некоторый момент времени реактивный ток направлен от зажима А к зажиму В (рис 12, а), то в это время ток в емкости обязательно направлен от зажима В к зажиму А.

Этот ток емкости, подойдя к точке А, оказывается тем источни­ком зарядов, которые нужны для образования реактивного тока индуктивности, а реактивный ток индуктивности, подходящий к точке В, является источником зарядов, образующих ток емкости. Так как эти токи равны по величине, то они полностью обеспечи­вают друг друга и, генератору не требуется снабжать реактивным током ни индуктивные, ни емкостные ветви схемы. Другими слова­ми, реактивные токи индуктивности и емкости текут за счет друг друга, в результате чего общий реактивный ток от генератора ра­вен нулю.

Явление совпадения по величине реактивных токов индуктив­ных и емкостных ветвей в параллельной цепи переменного тока называется резонансом токов. В режиме резонанса токов реактивные токи в ветвях могут оказаться очень большими и быть значительно больше тока всей цепи, текущего к ней от генератора. Такие соотношения могут быть, если активная проводимость цепи мала, а реактивные проводимости ветвей велики.

Колебательный контур в цепи с переменной э. д. с. Если в ре­жиме резонанса токов активная проводимость цепи уменьшится до нуля (при R₁ = 0), то и активный ток ее окажется равным нулю, это значит, что в этом случае от генератора вообще никакой ток не течет, так как в режиме резонанса токов он состоит из одной ак­тивной составляющей (I_р = 0).

Таким образом, переменные токи в ветвях (I_Р1 и I_Р2 ) существу­ют независимо от генератора, и его вообще можно отключить (рис. 13). Такую систему, состоящую из индуктивности и емкости, в которой может происходить колебательный процесс, назвали колебательным контуром, а колебания, происходящие в нем без помощи генератора,— свободными .

Существование в контуре переменных токов I_Р1 и I_Р2 без помо­щи генератора — это и есть свободный колебательный процесс, но начавшийся под влиянием переменной э. д. с, а не порции энергии, внесенной заряженным конденсатором. Это также процесс обмена энергией между индуктивностью и емкостью. Не затухает он из-за отсутст­вия потерь энергии, поскольку в ветвях нет активных сопротивле­ний.

В реальном колебательном контуре эти переменные токи без помощи генератора длительно существовать не могут.

Частота свободных колебаний в контуре называется собст­венной частотой колебательного контура.

Таким образом, колебательный контур представляет собой электрическую колебательную систему и в этом отношении подо­бен механической колебательной системе (маятнику), в которой тоже может совершаться свободный колебательный процесс, если ей сообщить некоторый запас энергии (толкнуть).

Условием возникновения в цепи резонанса токов является ра­венство реактивных проводимостей индуктивной и емкостной вет­вей, поэтому для получения его необходимо, изменяя емкость или индуктивность, добиться равенства в_L и в_с.

Так как при изменении частоты индуктивная и емкостная про­водимости изменяются взаимообратно, то даже при произвольных значениях индуктивности L и емкости С в цепи можно добиться - резонанса токов, подобрав частоту, при которой индуктивная про­водимость в_L окажется равной емкостной в_с. Эту частоту назы­вают резонансной и обозначают f_рез.

В идеальном колебательном контуре ее можно определить, имея в виду, что при этой частоте в_L = в_с. или

Из этого условия

, или 1=ωLC

Следовательно,

4π²f²_резLС=1, или f²_рез =

Окончательно f_рез =

где L — индуктивность контура (гн);

С— емкость контура (ф);

f_рез—резонансная частота (гц).

В реальном колебательном контуре значение резонансной ча­стоты несколько зависит и от величины активного сопротивления в нем.

Резонансная частота обязательно равна собственной частоте колебательного контура. Если при произвольных индуктивности и емкости мы добьемся резонанса токов, подобрав частоту тока пи­тающего генератора (например, f_рез = 400 гц), то колебания в контуре будут совершаться с частотой 400 гц (в контуре будут течь переменные токи I_p1 и I_p2 с частотой 400 гц). Уменьшив активное сопротивление контура до нуля и отключив его от генератора, мы добьемся того, что колебания станут самостоятельными (свобод­ными), но при этом частота их останется прежней (в контуре бу­дут совершаться свободные колебания с частотой 400 гц), это зна­чит, что собственная частота контура равна 400 гц.

Если цепь питается от генератора, создающего ток с частотой 50 гц, а резонанса мы добиваемся, изменяя в_L или в_с, то тем са­мым мы подбираем такую индуктивность или такую емкость, при которых собственная частота контура оказывается равной 50 гц (в_L = в_с при частоте 50 гц). На основании этих рассуждений, фор­мула резонансной частоты позволяет подсчитывать собствен­ную частоту колебательного контура. Из нее следует, что собствен­ная частота контура зависит от величины индуктивности и емкости и чем они больше, тем собственная частота меньше.

Из уравнения 2πf_рез = = , но так как к 2πf_рез =ω₀, то ω₀ =

Таким образом, резонанс токов — это явление, возникающее в параллельных цепях переменного тока при совпадении частоты то­ка питающего генератора с собственной частотой колебательного контура, а добиваются его двумя путями: либо собственную часто­ту контура подгоняя под частоту питающего тока (изменяя пара­метры контура), либо частоту питающего тока подгоняя под соб­ственную частоту контура.

Компенсация сдвига фаз

Так как всякая реактивная мощность создается реактивным то­ком, то емкость, являясь источником реактивного тока для индук­тивности, оказывается для нее и источником реактивной мощности. Поэтому после подключения емкости к цепи обмен энергией проис­ходит не между индуктивностью и генератором, а между индуктив­ностью и емкостью.

Если емкость недостаточно большая, то ток ее меньше реактив­ного тока индуктивности, и генератор освобожден от него не пол­ностью (цепь ведет себя как индуктивная). Если емкость слишком большая, то ее ток больше реактивного тока индуктивности и гене­ратор загружен, емкостным реактивным током (цепь, потребляя емкостный ток, ведет себя как цепь емкостная). Эти обстоятельст­ва можно использовать для компенсации сдвига фаз, создаваемого индуктивной нагрузкой (электродвигателями), то есть для увели­чения cos φ.

Для компенсации сдвига фаз достаточно параллельно индук­тивной нагрузке подсоединить емкость с таким расчетом, чтобы ток емкости был равен реактивному току нагрузки и генератор оказал­ся полностью освобожденным от реактивного тока и реактивной мощности.

Пример. Электрический двигатель мощностью 1,0 квт работает с коэффи­циентом полезного действия η = 0,83 и cos φ = 0,5. Подсчитать емкость конденса­тора, который нужно подключить к сети параллельно двигателю для того, что­бы полностью скомпенсировать сдвиг фаз, создаваемый двигателем. Напряжение сети 380 в.

Решение. Мощность, потребляемая двигателем из сети,

Р=

Реактивный ток двигателя I_р=Isin φ = 6,3 · 0,865=5,45 а. Следовательно, для полной компенсации сдвига фаз и обеспечения двигателя реактивным током ём­костной ток I с должен быть равен 5,45 а.

Емкостное сопротивление конденсатора Хс = = 69,7 ом.

Емкость конденсатора

C= 0.0000456 ф, или С= 45,6мкф

При частичной компенсации емкость разгружает генератор от реактивного тока не полностью. Величину необходимой при этом емкости определяют в зависимости от величины тока, который дол­жна обеспечить емкость. Для этого определяют реактивный ток I_р1 нагрузки до компенсации, реактивный ток I_р2 от источника тока по­сле компенсации и реактивный ток I_р, который должна обеспечить емкость. Очевидно I_P = I_P1 – I_P2.

По величине тока I_р определяют емкость конденсатора так же, как и при полной компенсации.

Пример. Определить емкость конденсатора, который необходим для увеличения cos φ до значения 0,9 в условиях, приведенных в предыдущем примере.

Решение. Реактивный ток двигателя до компенсации I_p1=5,45 а. Полный ток двигателя после компенсации

I₂ = , sinφ₂ = = 0.435

Реактивный ток двигателя после компенсации

I_Р2 =I₂ sin φ₂ = 3, 5·0,435 = 1,53а

Реактивный ток, который должен поступать в двигатель от конденсатора,

I_P=I_P1 – I_P2 =5.45a – 1.53a = 3.92a

Емкостное сопротивление конденсатора

Xc =

Емкость конденсатора

C = , или С = 32,8 мкф

Сравнив результаты этого и предыдущего примеров, мы видим, что для увеличения соs φ всего на 0,1 (с 0,9 до 1,0) емкость необхо­димо увеличить почти в полтора раза, поэтому практически полной компенсации добиваться нецелесообразно (емкость увеличивается сильно, а эффект от этого небольшой). Обычно cos φ увеличивают до значения 0,85—0,9. Кроме того, для различных категорий на­грузок устанавливается так называемый штрафной cos φ. Если на предприятии cos φ ниже штрафного, то к предприятию применяют меры экономического воздействия (штрафы, увеличение стоимости энергии и другие).

При использовании конденсаторов, специально предназначен­ных для компенсации сдвига фаз, расчет целесообразно вести по реактивной мощности, которую конденсаторы могут отдать индук­тивной нагрузке при рабочем напряжении, на которое они рассчи­таны. Рабочее напряжение и реактивная мощность, которую может отдать конденсатор, записаны на самом конденсаторе.

Технологическая карта№8

Измерение работы и мощности в цепи однофазного переменного тока.

Цель работы – ознакомиться с приборами (счетчиком и ваттметром), применяемыми для учета электроэнергии и измерения мощности, потребляемой в цепи однофазного переменного тока, а так же со схемами их включения.

Оборудование и аппаратура

Амперметр переменного тока на 5 А 1 шт

Вольтметр переменного тока на 150 В 1 шт

Однофазный фазометр на 127 В, 5 А 1 шт

Однофазный ваттметр на 127 В, 5 А 1 шт

Счетчик активной энергии однофазный СО на 127 В, 5 А 1 шт

Потенциометр на 250 Ом, 0,5 А 1 шт

Реостат регулировочный на 20 Ом, 4 А 1 шт

Панель с четырьмя потолочными патронами 1 шт

Лампы накаливания на 127 В, 150 Вт 4 шт

Рубильник двухполюсный на 127 В, 60 А 1 шт

Катушка индуктивности на 3 А 1 шт

Провода соединительные многожильные площадью

сечения 2,5 мм², длинной 1,5 м 14 шт

Источник переменного тока на 127 В, 50 Гц

Порядок выполнения работы

1. Ознакомиться с устройством счетчика и ваттметра и схемами их включения.

2. В ключить измерительные приборы в соответствии со схемой, показанной на рис. 14.

Рис 14. Схема соединений приборов для измерения мощности и энергии в однофазной цепи переменного тока и для поверки электрических счётчиков.

3. Измерить мощность, силу тока и напряжение. (Показания счетчика записывают в начале опыта и по истечении 10 мин. Нагрузка – чисто активная – лампа накаливания). Результаты записать в таблицу. Измерения выполнить при различном количестве ламп.

4. Повторить испытания при нагрузке, состоящей из индуктивной катушки и активного сопротивления. Результаты испытаний записать в таблицу. Измерения выполнять при различных силах тока.

5. Собрать схему, показанную на рис. 16, нате же нагрузки и проверить потребляемую мощность с помощью трех приборов.

6. Составить отчет.

Содержание отчета

1. Наименование отчета.

2. Параметры измерительных приборов и оборудования.

3. Схемы включения счетчика, ваттметра, амперметра и вольтметра для измерения мощности и электрической энергии.

4. Таблица с результатами измерения активной мощности и электрической энергии в цепи однофазного переменного тока.

5. Схема включения трех электроизмерительных приборов ( амперметра, вольтметра и фазометра) для измерения мощности.

6. Выводы.

Дополнительный материал к работе.

Электрической энергией называется работа, выполняемая электрическим током в течение какого-либо отрезка времени. Электрическую энергию измеряют электрическим счетчиком и определяют как произведение активной электрической мощности Р на время t:

W = Pt

За единицу энергии принят один джоуль (Дж): 1 Дж = 1 Вт х 1 с. Джоуль очень маленькая единица, поэтому в практике пользуются единицей в 3 600 000 раз большей – 1 кВт.ч. В этом случае активную электрическую мощность Р измеряют в киловаттах, а время t – в часах. 1 кВт/ч энергии равен 367 200 кгс.м, или 860 ккал.

Электрическая мощность определяется как работа, совершенная электрическим током в единицу времени, и за единицу ее принят 1 Вт = 1 Дж/ 1с. при переменном однофазном токе полную электрическую мощность измеряют в вольт-амперах

( В ^.А) и определяют по формуле

S = UI,

где U – действующее напряжение, В; I - действующая сила тока, А.

активную электрическую мощность однофазного переменного синусоидального тока измеряют в ваттах ( Вт ) и определяют по формуле

P = IU cos φ = I²r

Если приемники электрической энергии создают магнитное или электрическое поле, как, например, электродвигатели, сварочные трансформаторы и другие подобные установки, то кроме активной мощности в этом случае к потребителю электрического тока подводится реактивная мощность, которую обозначают Q, измеряют в вольт-амперах реактивных ( ВАр ) и определяют по формуле

Q = IU sin φ = I²x

Если известны активная и реактивная мощности, подводимые к потребителям электрической энергии, можно определить полную мощность электрической цепи, представляющую собой их геометрическую сумму

Полную электрическую мощность можно измерить при помощи вольтметра и амперметра. Измерять активную мощность в цепи однофазного переменного тока можно двумя методами: включением в цепь специального электроизмерительного прибора – ваттметра (рис. 15) или трех электроизмерительных приборов – вольтметра, амперметра и фазометра ( рис. 16). Во втором случае мощность подсчитывают перемножением показаний всех трех приборов.

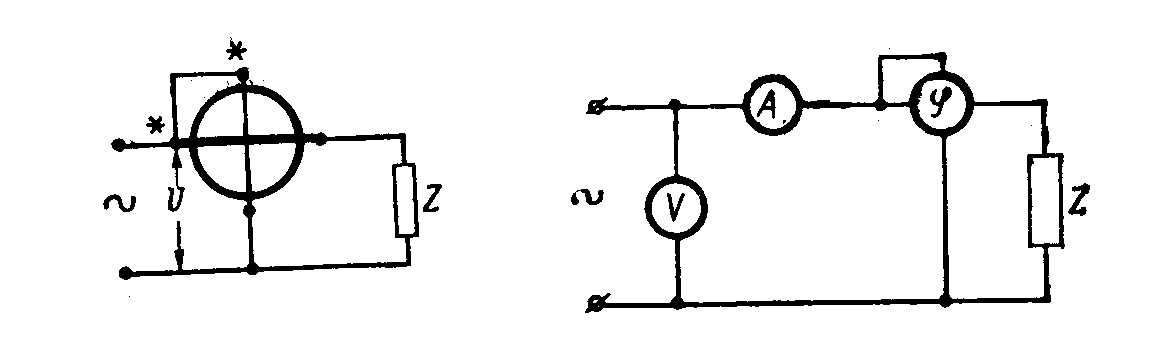
Рис 15Схема включения Рис 16Схема включения приборов

однофазного ваттметра. для измерения мощности в цепи

однофазного переменного тока.

Ваттметр снабжен двумя катушками: токовой, включаемой последовательно с потребителями, по которой проходит весь измеряемый ток (точно так же, как по катушке амперметра), и напряжения с добавочным сопротивлением, которая включена так же, как вольтметр, т.е. показания ваттметра – это произведение трех величин: напряжения U, силы тока I и коэффициента мощности cos φ. При подключении зажимов ваттметра к измеряемой цепи необходимо соединить начала и концы его обмоток в соответствии с направлением электрической энергии от генерирующей станции к потребителю. Начала ( генераторные зажимы) ваттметров обозначают звездочкой. Если нарушить этот порядок, стрелка ваттметра

будет отклоняться в противоположную сторону.

Технологическая карта№9

Исследование трехфазной системы при соединении осветительной

нагрузки звездой.

Цель работы. Научиться измерять токи, напряжения и мощности в трехфазных цепях. Практически ознакомиться с соотношениями между фазными и линейными величинами.

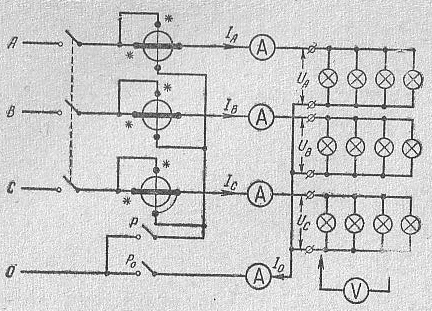
План работы. 1. Ознакомиться с силовым щитком и расположением зажимов на нём, выяснить номинальное линейное напряжение сети и мощность нагрузки.

2. Собрать цепь и после проверки руководителем подключить ее к сети.

3. Измерить токи, напряжение и мощности при различных положениях рубильников Р и Р₀ и при симметричной и несимметричной нагрузках.

4. Проделать необходимые вычисления, сравнить результаты и сделать выводы.

Пояснения к работе. В процессе подготовки к настоящей работе обратить внимание на соотношение между фазными и линейными величинами и способы измерения мощности в трёхфазных цепях.

Собрать цепь и замкнуть рубильники Р и Р₀. получится четырехпроводная трехфазная система с симметричной нагрузкой, соединенной звездой. Включив ее в сеть, измерить токи в каждой фазе, линейные и фазные напряжения и записать показания каждого ваттметра. После измерений подсчитать активную мощность нагрузки по показаниям амперметра и вольтметра и по показаниям ваттметров, а также отношения линейных напряжений к фазным. Активную мощность нагрузки по показаниям амперметров и вольтметра подсчитать как сумму мощностей в каждой фазе.

Мощность одной фазы подсчитать по уравнению:

P_ф = U_ф I_ф

так как cos φ = 1, активная мощность нагрузки по показаниям ваттметров равна сумме показаний ваттметров, то есть:

Р_изм = ∑ Р_w

где Р_w – показание одного ваттметра.

Результаты измерений и вычислений записать в таблицу.

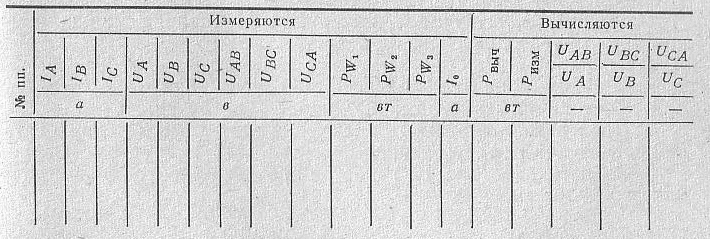
В этой таблице:

I₀ – ток в нулевом проводе;

Р_выч – активная мощность, вычисленная по показаниям амперметров и вольтметра;

Р_изм – активная мощность по показаниям ваттметров.

Размыкая рубильники Р и Р₀, пронаблюдать за изменением показаний приборов и накалом ламп соответственно.

Замкнуть рубильники Р и Р₀ и создать асимметрию нагрузки, выключив из одной фазы две лампы, а из другой три. Проделав те же измерения и вычисления, что и в предыдущем случае, результаты записать в ту же таблицу. Размыкая рубильник Р, проследить за изменением показаний ваттметров. При разомкнутом рубильнике Р₀ обратить внимание на изменения в накале ламп. Измерив и вычислив те же величины, что и в предыдущем случае, записать результаты в таблицу. При сравнении фазных напряжений оказывается, что:

U_A ≠ U_B ≠ U_c

Почему при симметричной нагрузке ток в нулевом проводе I₀ равен нулю? Почему при размыкании рубильников Р и Р₀ показания приборов и накал ламп не изменились?

Сравнить линейные токи при несимметричной нагрузке. Почему они не равны друг другу? Чем объяснить, что в этом случае ток в нулевом проводе I₀ не равен нулю? Подсчитать сумму показаний ваттметров при несимметричной нагрузке и разомкнутом рубильнике Р, сравнить её с Р_выч. Отличаются ли они друг от друга? Сделать вывод о применимости этого способа в трёхпроводной системе.

Почему при размыкании рубильника Р₀ изменяется накал ламп, если нагрузка несимметрична?

Сравнить между собой фазные напряжения в этом случае и сделать вывод о роли нулевого провода при несимметричной нагрузке.

Технологическая карта№10

Исследование трехфазной системы при соединении осветительной нагрузки треугольником.

Цель работы. Научиться измерять токи, напряжения и мощности в трехпроводных цепях.

План работы. 1. Ознакомиться с силовым щитком и расположением зажимов на нем, выяснить линейное напряжение сети, номинальное напряжение ламп и мощность нагрузки.

2. Проверить возможность включения этих ламп в данную сеть при соединении их треугольником.

3. Собрать цепь и после проверки руководителем подключить ее к сети.

4. Измерить токи, напряжения и мощности при симметричной и несимметричной нагрузках.

5. Проделать необходимые вычисления, сравнить результаты и сделать выводы.

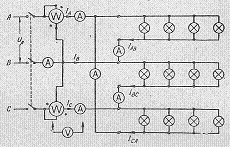
Пояснения к работе. В процессе подготовки к работе обратить внимание на соотношение между фазными и линейными величинами для соединения треугольником и на способ измерения мощности двумя однофазными ваттметрами. Измерив фазные и линейные токи, линейные напряжения и записав показания ваттметров, подсчитать активную мощность по показаниям амперметров и вольтметров ( Р_выч ) и по показаниям ваттметров ( Р_изм ). Результаты измерений и вычислений записать в таблицу.

Выключив в одной фазе две лампы, а в другой три, создать асимметрию в нагрузке, сделать измерения и вычисления. Результаты записать в таблицу.

Сравнить Р_выч и Р_изм. При наличии расхождений объяснить, чем это обусловлено. Сравнить накал ламп, включенных в разные фазы. Изменяется ли он при появлении асимметрии в нагрузке? Сравните соотношения между линией и фазными токами при симметричной и несимметричной нагрузке. Есть ли расхождения между ними? Если есть, то чем это объяснить?

Дополнительный материал к работам 9 и10.

Трехфазный ток

Основные понятия о трехфазном токе

Несколько электрических цепей, в которых действуют синусоидальные э. д. с. одинаковой частоты, сдвинутые относительно друг друга по фазе и создаваемые в одном источнике электрической энергии, в совокупности образуют многофазную систему.

В зависимости от количества цепей, составляющих многофазную систему, они могут быть двух - , трех - , четырех - , пяти - , и вообще сколько угодно фазными. Наибольший технико – экономический эффект получается при использовании трехфазной системы, поэтому в настоящее время во всем мире электрическая энергия используется почти исключительно только с помощью трехфазных систем.

Систему трех переменных токов одинаковой частоты и сдвинутых по фазе относительно друг друга, которые текут в трехфазной системе, называют трехфазным током.

Говоря о трехфазном токе, мы имеем в виду три обычных переменных тока, которые называются однофазными. Нагрузка, использующая трехфазный ток, потребляет одновременно три однофазных тока. Чтобы в цепи появился трехфазный ток, в ней должна действовать трехфазная э. д. с., понятие о которой аналогично понятию о трехфазном токе.

Чаще всего сдвиг по фазе между векторами э. д. с. или токов составляет 120^О.

Трехфазный ток обладает рядом преимуществ перед током однофазным.

1. Расход цветных металлов при электрификации какого – либо объекта трехфазным током значительно меньше, чем при электрификации его током однофазным (идет меньше металла на провода, обмотки и детали машин, пускорегулирующую аппаратуру и т. п.)

2. Трехфазные машины по устройству проще однофазных, а, следовательно, легче их, дешевле, более надежны в работе, могут эксплуатироваться менее квалифицированным персоналом.

3. Трехфазные системы экономически более выгодны и с технической стороны более целесообразны, чем однофазные.

Создателем трехфазных систем является русский инженер – электротехник М. О. Доливо – Добровольский, который разработал систему трехфазного тока (1888 г.), создал трехфазный двигатель (1889 г.), трехфазный трансформатор и впервые осуществил передачу энергии трехфазным током (1891 г.).

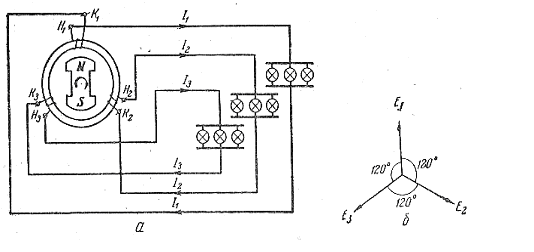
Для получения трехфазной э. д. с. достаточно на статоре генератора разместить три одинаковые катушки, расположив их под углом 120^О друг к другу, а в качестве ротора использовать постоянный магнит или электромагнит, питаемый постоянным током.

Магнитный поток вращающегося ротора, пересекая последовательно катушки статора, будет индуктировать в них три э. д. с. сдвинутые относительно друг друга по времени на ¹/₃ периода, а значит, и по фазе на 120^О. Векторная диаграмма э. д. с. изображена на рисунке.

Если к концам каждой катушки подсоединить нагрузку, то в цепях потекут токи, сдвинутые по фазе тоже на 120^О.

Такая несвязанная шестипроводная трехфазная система, то сравнению с однофазной, преимуществ не дает.

На рисунке видно, что если три обратных провода, по которым токи I₁, I₂ и I₃ возвращаются к генератору, заменить одним, система из шестипроводной превращается в четырехпроводную, которая называется связанной четырехпроводной трехфазной системой.

Генератор, питающий трехфазную систему, называется трехфазным. Токоприемники, присоединенные к трехфазному генератору, в совокупности образуют нагрузку, которую называют трехфазной.

Провода, соединяющие трехфазную нагрузку с трехфазным генератором, называют трехфазной линией.

Если в трехфазной системе действуют три одинаковые э. д. с., сдвинутые по фазе относительно друг друга на 120^О, и одинаковы комплексы сопротивлений отдельных частей трехфазной нагрузки, то такая система называется полностью симметричной. В такой системе токи так же одинаковы и сдвинута по фазе относительно друг друга на 120^О. Другими словами, в полностью симметричной системе действует симметричная система э. д. с. и получается симметричная трехфазная система токов.

Если система э. д. с. симметрична, а комплексы сопротивлений трехфазной нагрузки неодинаковы, то трехфазная система токов окажется несимметричной (токи друг другу не равны и сдвинуты на углы, отличающиеся от 120^О). Такая трехфазная система называется частично несимметричной.

Трехфазная нагрузка с неодинаковыми комплексами сопротивлений отдельных ее частей называется несимметричной. При рассмотрении явлений в трехфазных цепях мы будем предполагать, что система э. д. с., действующих в ней, симметрична.

Волновая диаграмма токов симметричной нагрузки приведена на рисунке она состоит из трех одинаковых синусоид сдвинутых по фазе относительно друг друга на 120⁰.

В четырехпроводной системе по четвертому обратному проводу течет ток, равный геометрической сумме токов I₁, I₂, I₃ или алгебраической сумме мгновенных значений (i_1, i_2, i₃ ). Если нагрузка симметрична, то в любой момент времени эта сумма равна нулю. Это хорошо видно на волновой диаграмме.

На ней в начальный момент времени i₁ = 0; i₂ = - 0,87 I_m; i₃ = 0,87 I_m;

∑ i = 0 – 0,87 I_m + 0,87 I_m = 0. В момент времени t₁ i₁ =0,5 I_m; i₂ = - I_m; i₃ = 0,5 I_m; ∑ i = 0,5 I_m + 0,5 I_m – I_m = 0.

Такие же результаты получатся и в моменты времени t₂ , t₃ и в любой другой момент времени. Это означает, что при симметричной нагрузке ток в четвертом обратном проводе отсутствует, надобность в нем отпадает и система становится трехпроводной.

На первый взгляд, кажется, что система стала разомкнутой, так как три тока текут на нагрузку, а обратного пути нет. Но нельзя забывать, что токи I₁, I₂, I₃ – переменные и не совпадают по фазе на 120⁰, поэтому если один ток в какой-либо момент времени направлен к нагрузке, то второй в это время может течь от нее. Распределение токов можно проследить с помощью волновой диаграммы. В начальный момент i₁ = 0; i₂ = - 0,87 I_m; i₃ = 0,87 I_m. Значит ток i₃ течет на нагрузку (положительный), доходит до точки О′, а дальше он составляет ток i₂ и возвращается к генератору. В момент t₁ i₁ =0,5 I_m; i₂ = - I_m; i₃ = 0,5 I_m. Два тока по 0,5 I_m сходятся в точке О′, образуют ток i₂ ив качестве этого тока возвращаются к генератору.

Таким образом, в трехпроводной системе происходит непрерывное согласованное распределение токов, и провода по очереди друг для друга являются обратными.

Если нагрузка несимметрична, то согласованности величин токов не будет, и поэтому необходим четвертый провод, то есть при несимметричной нагрузке и таком способе включения токоприемников система должна быть четырехпроводной.

Допустим, что в момент t₁ i₁ = 5 а ; i₃ =5 а, а i₂ не – 10 а, что бывает при симметричной нагрузке, а – 13 а. тогда токи i₁ и i₃, сойдясь в точке О′, образуют ток i₂, но он будет 10 а, а должен быть 13 а, поэтому и нужен четвертый провод, по которому пройдут недостающие в это время 3 а. этот ток как бы устраняет несимметрию между токами I₁, I₂, I₃, поэтому и называется уравнительным.