§ 6. Скорость движения точки

Важной характеристикой движения точки является ее скорость. Понятие скорости точки в равномерном прямолинейном движении относится к числу элементарных понятий.

Движение точки называется равномерным, если приращения радиуса-вектора точки за одинаковые промежутки времени равны между собой. Если при этом траекторией точки является прямая, то движение точки называется прямолинейным.

Для равномерно-прямолинейного движения

Δ r = υΔ t,

где v – постоянный вектор.

Вектор v называется скоростью прямолинейного и равномерного движения полностью его определяет.

Из соотношения (11.10) видно, что скорость прямолинейного и равномерного движения является физической величиной, определяющей перемещение точки за единицу времени. Из (11.10) имеем

υ=

Направление вектора V указано на рис. 37. Перейдем к рассмотрению неравномерного криволинейного дви­жения точки.

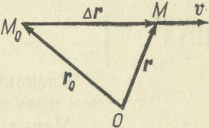
Пусть точка М произвольно движется по некоторой кривой. Пусть в момент t точка занимает положение М, а через весьма малый промежуток времени Δt она занимает положение М₁. Положение точки М определяется радиусом-вектором г, а положение точки М₁ — ради­усом-вектором г+Δг, равномерное прямолинейное движение точки из М в М^ можно охарактеризовать скоростью, равной отношению Δг к Δt, называемой средней скоростью:

υ_CP= .

Вектор υ_CP совпадает с направлением вектора Δг.

Переходя к пределу в (11.12), получим скорость в данной точке или в данный момент времени

υ= ,

или

υ=r

Здесь и далее производные по времени обозначаются по Ньюто­ну, например, г и т. д.

Следовательно, скорость в данной точке равна первой производ­ной по времени от радиуса-вектора точки.

Так как секущая в пределе переходит в касательную, то ско­рость в данной точке направлена по касательной к траектории в сторону возрастания дуг.

§ 7. Скорость точки в прямоугольной декартовой системе координат

Если движение точки задано координатным способом: х = х (t), у = у (t), z=z (t), то скорость точки определяется по ее проекциям на оси координат. Действительно, разложим вектор скорости и радиус-вектор г по ортам координатных осей (рис. 38). Получим

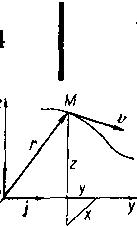
г = iх + jу + kz,

υ=iυ_X+jυ_Y+kυ_Z ,

где х, y, z — координаты движущейся точки, υ _х, υ _y, υ_z — проекции скорости на оси координат. По определению скорости имеем

υ=r

Подставляя в эту формулу значения υ и г из (11.14), получим

iυ_X+jυ_Y+kυ_Z= iх + jу + kz,

откуда

υ_X=x, υ_Y=y, υ_Z=z

Следовательно, проекции скорости на оси координат равны первым производным по времени от соответствующих координат точки. Модуль скорости определяется по формуле

υ= ,

или

υ= .

Направление скорости определяется по направляющим косинусам:

cos(υ^i)= , cos(υ^j)= , cos(υ^k)=

§ 9. Скорость точки в полярных координатах

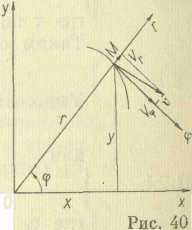
Если движение точки в плоскости Оху задано в поляр­ных координатах: г = г (t); φ = φ (t), то, выражая де­картовы координаты через полярные (рис. 40), получим х = r cos φ, y= r sinφ. Проекции скорости υ на оси де­картовых координат будут

υ = x = r cos φ – r sin φ = υ cos φ- υ φ sin φ,

υ = y= r sin φ + rφ cos φ= υ sinφ + υ cos φ,

_{где υ = г — проекция скорости на радиальное направление r, υ = rφ — проекция скорости на трансверсальное направление φ. Модуль скорости}

_{υ= r}²_{+ r}²_φ²