Момент силы относительно точки и оси. Главный вектор и главный момент. Пара сил. Момент силы относительно точки

Моментом силы относительно точки называется векторное произведение радиус-вектора точки приложения силы на силу. Итак, по определению (рис. 12),

Обозначая длину перпендикуляра, опущенного из центра момента на линию действия силы, через h (величину h в дальнейшем будем называть плечом), можно модуль вектора Мо (F) представить в виде произведения Fh, т. е.

|М₀(F)| =М₀(F) = Fh.

Таким образом, момент силы относительно точки — это вектор, направленный перпендикулярно к плоскости, содержащей силу и точку, в ту часть пространства,.

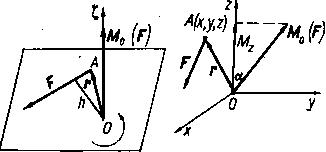
Для аналитического определения момента силы относительно точки выберем произвольную систему координат О_xyz с началом в точке О (рис. 13) и обозначим проекции радиуса-вектора г и силы F на координатные оси О_x, О_Y, О_z, соответственно через х, у, z и X, У, Z. Заметим, что проекции х, у, z радиуса-вектора г точки прило­жения силы одновременно означают координаты этой точки. Тогда, спроектировав обе части векторного равенства (1.15) на оси координат, получим выражение момента силы относительно точки в анали­тической форме в виде трех его проекций на координатные оси:

,

.

Теорема о моменте равнодействующей системы

сходящихся сил (теорема Вариньона)

Момент силы относительно оси

Моментом силы относительно оси называется проекция на ату ось момента силы относительно произвольной точки на оси. Момент силы F относительно оси Оz обозначается через М_z (F). Таким обра­зом,

М

Момент силы относительно оси, как будет показано в динамике, является физической величиной, характеризующей вращательное движение твердого тела.

Согласно определению, моменты силы относительно координат­ных осей выражаются величинами (1.18), т. е. соответственно равны проекциям

М М_У(F) = zХ -хZ; М

Укажем практический способ определения момента силы относи­тельно оси.

Главный вектор и главный момент системы сил

Главным вектором R системы сил F₁,F₂ … , F_n называется векторная сумма этих сил, т. е.

R=

Таким образом, главный вектор системы сил можно определить геометрически с помощью многоугольника сил.

Аналитически главный вектор определяется тремя своими проекциями на координатные оси;

R

R

R

Главным моментом Мо системы сил F_1: F₂, ..., F_n относительно точки называется векторная сумма моментов этих сил относительно этой точки, т. е

M

Таким образом, главный момент системы сил относительно точки можно определить геометрически с помощью многоугольника момен­тов этих сил относительно данной точки.

Аналитически главный момент относительно точки определяется тремя своими проекциями на координатные оси:

M

M

M

или

; ;

Заметим, что понятия главного вектора и равнодействующей системы сил не тождественны. Как мы увидим в следующей главе, не всякая система сил имеет равнодействующую. Если же система сил и приводится к равнодействующей, то последняя, хотя геометрически и равна главному вектору, но имеет вполне определенную линию действия, в то время как главный вектор (также и главный момент) является свободным вектором.