§ 2. Уравнение Мещерского

При выводе уравнения Мещерского будем исходить из следующих соображений. Пусть точка, масса которой изменяется с течением вре­мени, в момент t имела массу m (t) и абсолютную скорость υ. Тогда количество движения этой точки в момент t равно

k = m(t) υ.

Пусть далее к данной точке за время dt присоединилась другая точка с массой dm (t), обладающая в момент присоединения конечной абсолютной скоростью u.

Тогда в момент t+dt образуется одна точка с массой m (t)+ dm (t), имеющая скорость υ +dυ и количество движения

Поскольку в момент t количество движения указанной системы равнялось m (t) υ + udm, то приращение количества движения будет равно

С другой стороны, dk = dS, где dS — элементарный импульс равнодействующей силы F. Следовательно,

откуда

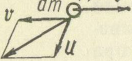
где u — υ = υ_r — относительная скорость присоединенной к точке массы (рис. 138). Тогда

где

называется реактивной силой.

Следовательно,

Это дифференциальное уравнение движения точки переменной мас­сы называется уравнением Мещерского. Оно было выведено в его ма­гистерской диссертации, опубликованной в 1897 г.

Основной закон движения точки переменной массы, выражаемый уравнением (111.273). может быть сформулирован следующим обра­зом: при движении точки переменной массы в любой момент времени произведение массы этой точки на ее ускорение равно геометрической сумме действующих на точку сил F и реактивной силы Ф.

Если относительная скорость υ_r= u —υ отделяющихся (или присоединяющихся) частиц будет равна нулю, т. е. тело переменной массы не отбрасывает отделяющиеся от него частицы, а просто распа­дается, то реактивная сила в этом случае будет равна нулю и из урав­нения Мещерского (111.310) видно, что движение такой точки пере­менной массы выражается уравнением

mυ=F,

которое имеет вид уравнения движения материальной точки постоян­ной массы, в котором масса m точки будет переменной величиной, заданной функцией времени.

Проектируя обе части уравнения (111.310) на оси неподвижной системы координат Охуz, получим три скалярных уравнения:

Для подавляющего числа случаев современной ракетодинамики можно принять гипотезу Циолковского, заключающуюся в том, что вектор относительной скорости υ_r отбрасываемых частиц постоянен по величине, лежит на касательной к траектории движения точки переменной массы и направлен в сторону, противоположную вектору скорости v движения излучаемой точки переменной массы, т. е.

υ_r=- υ_rτ_r

где

υ_r= =const,

τ— единичный вектор касательной к траектории движения точки переменной массы.

В этом случае уравнение движения (111.310) примет вид

mυ=F- υ_rm(t) τ.

В современной ракетодинамике большой интерес представляет случай прямолинейного восходящего движения ракеты, когда в урав­нении (111.310) равнодействующая внешних сил F представляет собой векторную сумму двух сил F₁+ F₂. Сила F₁ = mа пропорциональна переменной массе движущейся точки; сила F₂ — сила сопротивления, зависит от скорости движения точки. Эта задача впервые была по­ставлена и частично изучена И. В. Мещерским для двух случаев: когда сила сопротивления F₂ является линейной функцией скорости точки и когда F₂ пропорциональна квадрату скорости ее движения. Уравнение (111.311) при F = F₁ + F₂, F₁ = mа примет вид

mυ=mа — υ_rmτ + F₂.

Если пренебречь силами сопротивления F₂ и представить массу тела в виде m = m₀ ƒ (t), где m₀ — масса точки вначале, т. е. при t = 0; ƒ (0) = 1, то это уравнение примет вид

где a — известная функция, зависящая как от времени t, так и от расстояния.

В настоящее время функцию ƒ (t) в большинстве случаев принимают при линейном законе изменения массы в виде

ƒ (t)= 1 — αt,

а при показательном законе изменения массы в виде

ƒ (t)=e^-αt.

Таким образом, массу движущейся точки выражают в двух видах:

m(t)= m₀(1 — αt),

m(t)= m₀ e^-αt.

В этом случае реактивная сила Ф = υ_rm будет равна

Ф⁽¹⁾= - α m₀υ_r

либо

Ф⁽²⁾= - α m₀ e^-αt υ_r.

Так как по гипотезе К. Э. Циолковского υ_r = соnst, то величина реактивной силы Ф⁽¹⁾ будет постоянной, а силы Ф⁽²⁾ — переменной, уменьшающейся по тому же закону, что и масса движущейся точки.

Таким образом, ускорение вызванное

силой Ф⁽¹⁾, действующей на точку, переменной массы, будет стечением

времени численно возрастать, а ускорение бу­дет оставаться постоянным.

Если F = 0, то υ = υ₀. Отсюда получаем закон инерции для точки переменной массы.

Когда отсутствуют внешние силы, точка переменной массы будет двигаться прямолинейно и равномерно со скоростью υ₀ (при υ₀≠ 0) или находиться в покое (при υ₀= 0), если относительная скорость отделения ее частиц равна нулю, т. ё. υ_r = 0.

Если F = 0 и абсолютная скорость отделяющихся частиц и так­же равна нулю, т. е. при υ_r = — υ получим

mυ= - υm, или (mυ)=0.

Интегрируя и обозначая постоянную интегрирования С = m₀ υ₀,

получим mυ = m₀ υ₀, откуда

где m₀ и υ₀ — масса точки и скорость ее в момент t = 0, принятый за начальный.

Видим, что при отсутствии внешних сил и абсолютной скорости отделения частиц, равной нулю, скорость υ излучающей точки переменной массы увеличивается обратно пропорционально умень­шению массы излучаемой точки.