§ 5. Не вполне упругий удар двух шаров

Рассмотрим не вполне упругий удар двух шаров. Не вполне упру­гим ударом называется такой удар, которому соответствует коэффи­циент восстановления k< 1.

Решая совместно систему уравнений (111.298) и (111.299), най­дем скорости шаров в конце рассматриваемого удара:

следовательно,

§ 6. Косой удар двух шаров

Удар называется косым, если скорости соударяющихся шаров не направлены по прямой, соединяющей их центры тяжести. Пусть два шара движутся со скоростями υ₂ и υ₂ (рис. 135).

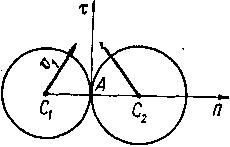
Проведем общую касательную τ в точке А и нормаль n. Для изу­чения косого удара данных тел воспользуемся уравнением (111.298) в проекциях на указанные направления касатель­ной и нормали

По определению коэффициентов восстановления

На основании (111.293)

Из указанных уравнений найдем искомые скорости u_1τ, u_1n, u_2τ, u_2n тел после удара.

§ 7. Неупругий удар двух шаров

Неупругому (пластическому) удару соответствует коэффициент вос­становления k = 0. Неупругий прямой удар двух тел характери­зуется тем, что после удара тела движутся вместе как единое целое с одинаковой скоростью u₁ = u₂ = u.

Полагая в (111.298) u₂ = u₁ = u, найдем скорость тел в конце удара

и, следовательно,

ДИНАМИКА ТОЧКИ ПЕРЕМЕННОЙ МАССЫ

§ 1. Общие замечания

Под точкой переменной массы подразумевается геометрическая точка, в которой сосредоточена конечная масса т (I), изменяющаяся во время движения по определенному закону.

Так, при движении масса ракеты изменяется за счет выбрасывае­мых из нее продуктов сгорания. Поступательное движение этой ра­кеты может быть легко сведено к изучению движения какой-либо ее характерной точки. Дифференциальные уравнения движения этой точки будут представлять собой дифференциальные уравнения дви­жения точки переменной массы m (t).

Другим примером тела переменной массы может служить рулон газетной бумаги, так как при разматывании его на валу печатной машины масса его уменьшается.

Классическим примером динамической задачи, где необходимо учитывать изменения масс движущихся тел, является шахтный подъ­емник.

При опускании груза в шахту длина подъемного каната, а следо­вательно, и его масса увеличиваются за счет уменьшения массы кана­та, навитого на барабане. При подъеме груза наблюдается обратное явление.

Можно привести еще ряд примеров, когда масса тел при движении увеличивается. Так, при падении на Землю метеоритов масса Земли увеличивается. Масса Солнца в результате лучеиспускания умень­шается, а при присоединении космической пыли возрастает.

Основоположник механики тел переменной массы И. В. Мещерский (1859—1935) в основу своих исследований положил гипотезу близкодействия отбрасываемых частиц. При этом допускалось, что при отделении от тела частицы происходит удар, при котором за весьма малый промежуток времени отбрасываемая частица получает отно­сительную скорость, и тогда дальнейшее взаимодействие отбрасы­ваемой частицы с данным телом прекращается.

Пользуясь этой гипотезой, И. В. Мещерский вывел основное урав­нение движения точки переменной массы.

Существенно подчеркнуть, что здесь речь идет о движении тел переменной массы в пределах классической механики. При этом масса тел определяется обычным путем и изменяется по заранее задан ному закону. Поэтому переменная масса, которая рассматривается в данной главе, не имеет ничего общего с переменной массой, фигурирующей в теории относительности.