Модуль 1

«Электростатика. Магнитостатика. Электрический постоянный ток.»

Домашнее задание №1: выдача – 1 неделя, сдача – 07- 08 неделя

Варианты тематических задач, общих для всех студентов группы, с указанием литературного источника из раздела "1. ЛИТЕРАТУРА"

[6] №2.05

1. Два небольших одинаково заряженных шарика m массы подвешены в вакууме к одной точке на непроводящих электрический ток, одинаковой длины нитях. Найти dq/dt скорость утечки заряда с каждого шарика в момент времени, когда эти нити образуют между собой малый α угол, если модуль v вектора v скорости сближения шариков известен и постоянен. Ответ: dq/dt = - 1,5v(2πε₀ mgα)^1/2, где ε₀ - электрическая постоянная; g - стандартное ускорение свободного падения.

[6] №2.33

2. Внутри шара, заряженного равномерно с ρ объёмной плотностью, на известном a расстоянии от O центра этой заряженной сферы, равного модулю a вектора, имеется незаряженная

сферическая полость. Пренебрегая влиянием вещества заряженного шара, найти модуль E и направление вектора E напряжённости электростатического поля внутри полости. Ответ: E = ρa/3ε₀ ; E = ρa/3ε₀, где ε₀ - электрическая постоянная.

[6] №2.53

3. Электрический диполь с известным и постоянным p модулем вектора p дипольного электрического момента

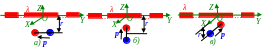
находится на r расстоянии от длинной прямой нити, заряженной равномерно с λ линейной плотностью. Найти вектор F силы, действующий на этот электрический диполь, если вектор

p дипольного электрического момента ориентирован: а) вдоль нити и параллельно OY оси;

б) перпендикулярно нити и параллельно OZ оси; в) перпендикулярно нити и параллельно

OX оси. Ответ: а) F = 0; б) F = - λp/2πε₀r²; в) F = λp/2πε₀r², где ε₀ - электрическая постоянная;

p - вектор дипольного электрического момента, ориентированный в каждом варианте а), б) и в) согласно схеме в условии задачи.

[6] №2.58

4. Потенциал φ электростатического поля внутри заряженного шара зависит только от r расстояния рассматриваемой точки до O центра шара и не зависит от направления r радиуса - вектора этой рассматриваемой точки. Зависимость потенциала электростатического поля внутри заряженного шара имеет вид: φ = ar² + b, где a, В/м² и b, В - известные постоянные. Пренебрегая влиянием вещества, найти распределение ρ(r) объёмной плотности свободного заряда внутри шара.

Ответ: ρ = - 6aε₀, где ε₀ - электрическая постоянная.

[6] №2.84

5. Точечный сторонний q заряд находится в O центре шара R радиуса, имеющего ε₁ диэлектрическую проницаемость. Этот шар окружен безграничным диэлектриком с ε₂ диэлектрической проницаемостью. Определить поверхностную σ_p плотность связанных зарядов на сферической поверхности границы раздела двух диэлектриков.

Ответ:

[6] №2.105

6. Пластинка h толщиной из однородного статически поляризованного диэлектрика находится в вакууме внутри плоского конденсатора, обкладки которого находятся на d расстоянии друг от друга и соединены между собой проводником. Вектор

P поляризованности диэлектрика перпендикулярен плоскости поверхности пластинки. Найти векторы E₁, E₂ и D₁, D₂ соответственно напряжённости электростатического поля и электрического смещения внутри и вне этой диэлектрической пластины между обкладками плоского конденсатора.

Ответ:

; ;

[6] №2.138

7. Плоский воздушный конденсатор с S площадью и d расстоянием между пластинами поместили во внешнее однородное электростатическое поле с вектором E напряжённости этого электростатического поля перпендикулярного поверхностям пластин. Затем пластины замкнули проводником, после чего проводник убрали и

конденсатор перевернули на 180⁰ вокруг OO′ оси, которая перпендикулярна вектору

E напряжённости внешнего однородного электростатического поля. Найти A′ работу внешних сил, совершённую против сил электростатического поля, при этом повороте конденсатора, а также найти q количество электричества, которое протекло через проводник при повторном замыкании им пластин, совершённое после поворота конденсатора.

Ответ: A′ = 2E²ε₀Sd; q =2Eε₀S, где ε₀ - электрическая постоянная.

[6] №2.150

8. Плоский воздушный конденсатор C емкостью, между обкладками которого находится в 1 - ом случае металлическая, а во 2 - ом случае стеклянная пластина ζd толщиной в обоих случаях, где d - расстояние между обкладками конденсатора, подключили к внешнему постоянному U напряжению. Затем этот

воздушный конденсатор, между обкладками которого находится пластина, отключили от внешнего напряжения, после чего медленно извлекли пластину из зазора конденсатора. Найти A₁′, A₂′ работу внешних сил, совершённую против сил электростатического поля в 1 - ом и во 2 - ом случаях, при извлечении пластины, а также найти, во сколько k₁ , k₂ раз увеличивается U₁, U₂ напряжение между обкладками конденсатора после извлечения пластины по сравнению с внешним постоянным U напряжением.

;

;

Ответ:

;

[6] №2.153 9. В цилиндрический конденсатор, подключённый к внешнему постоянному U напряжению, с R₁, R₂ радиусами обкладок вводят длинный трубчатый диэлектрик с ε диэлектрической

проницаемостью, заполняющий практически весь зазор между этими обкладками. Найти F модуль и направление вектора F силы электростатического поля, который действует на трубчатый диэлектрик.

Ответ: F = πU²ε₀(ε - 1)/ln(R₂ /R₁); вектор F силы электростатического поля, который действует на трубчатый диэлектрик, направлен противоположно OY оси.

[6] №2.158

10. При каком значении R_x сопротивления оконечного резистора входное R_AB сопротивление не зависит от n количества ячеек, где каждая i - ая ячейка состоит из 2 - ух резисторов R и 2R сопротивлением.

[6] №2.166

11. Два длинных прямых параллельных провода с l расстоянием между осями этих проводов, намного большем а радиуса каждого провода, находятся в однородной слабо проводящей среде с ρ удельным сопротивлением. Найти модуль j и направление вектора j удельной плотности тока в точке пространства между проводами, равноудалённой на r расстояние от осей проводов, если напряжение

м

Ответ:

;

ежду этими проводами равно U, а также найти R₀ сопротивление среды между проводами на их единицу длины.

[6] №2.174

12. Зазор между обкладками плоского конденсатора, к которому подключено постоянное U напряжение, заполнен двумя диэлектрическими слоями толщиной d₁, d₂, относительными ε₁, ε₂ диэлектрическими проницаемостями и удельными

ρ₁, ρ₂ сопротивлениями. Определить поверхностную σ плотность свободных зарядов на границе раздела диэлектрических слоёв и условие, при котором σ = 0.

σ = 0, когда ε₂ρ₂ = ε₁ρ₁.

;

Ответ:

[6] №2.177

13. Конденсатор C ёмкостью в начальный момент t₀ = 0 времени имел начальное U_н напряжение. Вывести выражение зависимости U напряжения на конденсаторе от t времени при подключении через резистор R сопротивлением с помощью Кл ключа источника с ЭДС, равной ε.

Сопротивление подводящих проводников и внутреннее сопротивление источника ЭДС считать равными нулю.

Ответ: U = ε - (ε - U_н)e^-t/τ, где τ = RC - постоянная времени зарядки конденсатор C ёмкостью через резистор R сопротивлением.

[6] №2.185

14. Разрядный промежуток дугового разряда представляет собой нелинейное R_д сопротивление с зависимостью U_д напряжения от тока I_д силой, указанной на рисунке. Найти максимальную величину R_max сопротивления резистора, соединенного последовательно с дугой, при котором дуга ещё будет гореть, если эту систему подключить к постоянному внешнему U₀ = 85 В напряжению.

Ответ: дуга будет гореть до тех пор, пока нагрузочная характеристика цепи U_д = U₀ - RI_д не станет касательной к графической зависимости U_д напряжения от тока I_д силой дугового разряда, что происходит при R_max ≈ 11 Ом. При постоянном внешнем U₀ напряжении, равном 85 В, и величине R сопротивления резистора, соединенного последовательно с дугой, равном R_max ≈ 11 Ом, напряжение U_д дугового разряда равно ≈ 67 В при токе I_д силой этой дуги, равном ≈ 3 А.

[6] №2.217

15. С К катода, представляющего собой большую пластину, поток е электронов в вакууме с пренебрежимо малой начальной скоростью направляется к А аноду, представляющему собой тоже большую пластину, вследствие того, что φ потенциал зависит от

z расстояния от К катода согласно следующему уравнению:

φ = az^4/3, где a , В/м^4/3 - известная положительная постоянная. Определить: а) распределение ρ(z) объёмной плотности

пространственного заряда е электронов в z расстояния от К катода; б) модуль j вектора

j плотности тока между К катодом и А анодом.

Ответ: , где знак "-" учитывает наличие между А анодом и К катодом отрицательного пространственного заряда е электронов; .

[6] №2.234

16. Ток I силой течёт по длинному прямому проводнику, сечение которого имеет форму тонкого полукольца R радиуса и расположенному в вакууме. Найти модуль B и направление вектора B индукции магнитного поля на

OO′ оси этого проводника.

Ответ: B = μ₀I/π²R; вектор B индукции магнитного поля на OO′ оси проводника направлен по OY оси.

[6] №2.250

17. Длинный соленоид в вакууме имеет R радиус сечения и n витков на единицу длины. По нему течёт постоянный ток I силой. Найти B', B модули векторов индукции магнитного поля на оси в функции h расстояния от торца соответственно B' вне и B внутри этого соленоида. Изобразить примерный график зависимости B' модуля вектора B' индукции магнитного поля на оси длинного соленоида в функции h' расстояния от торца вне соленоида, отнесённого к R радиусу этого соленоида, т.е. в зависимости от h' /R, а также изобразить примерный график зависимости B модуля вектора B индукции магнитного поля в функции h расстояния от торца вне соленоида, отнесённого к R радиусу этого соленоида, т.е. в зависимости от h /R.

Ответ:

, где B'_M' - модуль вектора B'_M' индукции магнитного поля в M' точке на оси длинного соленоида в функции h' расстояния от торца вне этого соленоида.

, где B_M - модуль вектора B_M индукции магнитного поля в M точке на оси длинного соленоида в функции h расстояния от торца внутри этого соленоида;

примерный график зависимости B'/B₀ B/B₀ отношения модулей векторов

B', B индукции магнитного поля к модулю B₀ = μ₀nI индукции магнитного поля в центре на оси длинного соленоида соответственно вне и внутри этого соленоида имеет вид возрастающей

функции от отрицательного h/R значения левее торца длинного соленоида до положительного h/R значения внутри этого соленоида.

[6] №2.282

18. Вдоль длинного тонкостенного трубчатого проводника R радиуса, расположенного в вакууме, течёт постоянный ток I силой. Какое p давление испытывают стенки трубчатого проводника и в какую сторону направлено это давление?

Ответ: p = μ₀I²χ/8π²R², где μ₀ - магнитная постоянная; p давление направлено к оси трубчатого проводника, т.е. стенки трубчатого проводника испытывают сжимающее усилие.

[6] №2.286

19. Вдоль медного прямого проводника R радиусом течёт ток I силой. Найти φ₁ - φ₂ разность потенциалов между OZ осью проводника и его поверхностью. Концентрация n_e электронов проводимости у меди известна. Ответ: φ₁ - φ₂ = μ₀I²/4π²Rn_ee, где e - элементарный заряд;

μ₀ - магнитная постоянная.

[6] №2.292

20. Постоянный магнит R радиуса имеет форму тонкого диска, намагниченного вдоль OO′ оси этого магнита. Оценить значение и направление молекулярного тока I_мол силой, текущего по ободу диска, если известен модуль B вектора B индукции магнитного поля на оси OO′ этого диска в точке M, отстоящей на h расстоянии от O центра диска.

Ответ: I_мол = 2B_Mh³/μ₀R², где μ₀ - магнитная постоянная; молекулярный ток I_мол силой течёт по ободу диска по "часовой стрелке".

[6] №2.295

21. Вдоль длинного цилиндрического провода R радиуса, сделанного из однородного парамагнетика с магнитной χ восприимчивостью, течёт постоянный ток I силой. Определить модуль j_мол, направление вектора j_мол плотности молекулярного тока в зависимости от r расстояния до OO′оси

цилиндрического провода, а также определить поверхностный I_{мол.пов.} и объёмный I_мол.. молекулярный ток в этом цилиндрическом проводе и их направление.

Ответ: j_мол = I²χ/πR²k, где k - единичный вектор по OZ оси; I_{мол.пов} = I_мол. = Iχ. Токи I_{мол.пов.} и I_мол силой направлены противоположно.

[6] №2.308

22. Длинный тонкий стержень, сделанный из однородного парамагнетика с магнитной

χ восприимчивостью и S площадью поперечного сечения расположен вдоль OY оси катушки с током. Один конец этого стержня расположен внутри катушки, где модуль вектора B индукции магнитного поля равен B, а другой конец стержня расположен в области, где магнитное поле практически отсутствует. Найти модуль F и направление вектора F силы, с которой катушка действует на этот стержень.

Ответ: F = χSB ²/2μ₀, где μ₀ - магнитная постоянная; вектор F силы, с которой катушка действует на стержень направлена по OY оси, т.е. стержень втягивается внутрь катушки.

Модуль 2

"Переменные электрические и магнитные поля. Уравнения Максвелла. Движение заряженных частиц в электрических и магнитных полях","Электромагнитные волны", "Волновые свойства света"

Домашнее задание №2: выдача – 1 неделя, сдача – 13-14 неделя

Варианты тематических задач, общих для всех студентов группы, с указанием литературного источника из раздела "1. ЛИТЕРАТУРА"

[6] №2.334

1. Непроводящее тонкое кольцо m массы, имеющее q заряд, может свободно вращаться вокруг своей OO′ оси. В начальный момент t₀ = 0 времени включили однородное магнитное поле,

вектор B индукции которого перпендикулярен плоскости кольца. Известна функция B(t) зависимости модуля от t времени вектора B(t) индукции магнитного поля. При этом направление этого

вектора B(t) индукции магнитного поля не меняется. Найти зависимость вектора ω угловой скорости вращения кольца от изменяющегося во t времени вектора B(t) индукции магнитного поля.

Ответ: ω = - qB(t)/m, где направление вектора ω угловой скорости вращения кольца определяется знаком его q заряда и направлением вектора B(t) индукции магнитного поля.

[6] №2.347

2. Ток i0 силой течёт по длинному сверхпроводящему соленоиду l длиной. Найти ток I силой в соленоиде после того, как его растянули, увеличив длину на ζl величину.

Ответ: I = I₀(1 + ζ).

[6] №2.377

3. В двух проводящих круглых контурах, находящихся в вакууме, с a, b радиусами и индуктивностями L₁, L₂, текут в одном направлении, например, против вращения часовой стрелки, токи I₁, I₂ силой. Центры O колец совпадают, а OO′ ось 1 - ого кольца составляет υ угол с OO′′ осью 2 - ого

кольца. Найти W₁₂ магнитную энергию взаимодействия двух проводящих круглых контуров,

если a<< b. Ответ: W₁₂ = μ₀πa²cosυI₁I₂/2b, где μ₀ - магнитная постоянная.

[6] №2.378

4. Пространство между двумя концентрическими металлическими сферами заполнено слабо проводящей средой с ρ удельным сопротивлением и ε диэлектрической проницаемостью. В некоторый момент t времени заряд на внутренней сфере равен q₊ . Найти: а) связь между векторами плотностей токов j проводимости и j_см смещения; б) силу I_см тока смещения в этот момент t времени через произвольную

поверхность в слабо проводящей среде, охватывающую внутреннюю сферу.

Ответ: j = - j_см; I_см = - q₊ /ε₀ερ, где знак "-" учитывает противоположное направление силы I_см тока смещения вектору плотности тока j проводимости в случае численного положительного значения q₊ заданного в условии задачи свободного заряда на внутренней сфере в некоторый момент t времени; ε₀ - электрическая постоянная.

[6] №2.382

5. По длинному соленоиду с R радиусом витка и n количеством витков на единицу длины этого соленоида, находящемуся в вакууме, течёт переменный ток I = I_msinωt силой, где I_m, ω - заданные соответственно амплитуда и циклическая частота переменного тока. Определить модуль j_см и направление вектора j_см плотности тока смещения как функцию r расстояния от OO′ оси соленоида внутри при r<R и вне при r>R этого соленоида.

Ответ: j_см = ε₀μ₀nI_mω²r sinωt/2 при r<R; ; j_см = ε₀μ₀nI_mω²R²sinωt/2r при r<R; вектор j_см плотности тока

смещения коллинеарен и направлен в одну сторону с вектором E_в электрического вихревого поля, т.е. по касательной к окружности, плоскость которой перепендикулярна оси длинного соленоида; ε₀ - электрическая постоянная; μ₀ - магнитная постоянная.

[6] №2.385

6. Точечный q заряд движется с нерелятивистским постоянным значением модуля v вектора v скорости в направлении OY оси. Точка A находится на Ок окружности, плоскость которой

перпендикулярна OY оси. Определить выражение вектора H напряжённости магнитного поля в точке A, как функцию R радиуса - вектора этой A точки и вектора v скорости q заряда.

Ответ: Н = q[vR]/4πR³.

[6] №2.392

7. Большая пластина из однородного диэлектрика, имеющего относительную ε диэлектрическую проницаемость, движется в вакууме поступательно параллельно OYZ плоскости с нерелятивистским значением модуля v вектора v скорости, направленного под φ углом к OY оси, в однородном магнитном поле с вертикально направленным и известным B модулем вектора B индукции магнитного поля. Найти P модуль и направление вектора P поляризованности диэлектрика,

а также определить, на каких гранях пластины образуется связанный заряд, его знак и σ_p поверхностную плотность.

Ответ: P = ε₀(ε - 1)vBsinφ/ε; вектор P = ε₀(ε - 1)[vB]/ε поляризованности диэлектрика лежит в OXY плоскости и параллелен OX оси; на 1 - ой грани пластины, параллельной

OYZ плоскости,образуется положительный связанный заряд σ_p+ = ε₀(ε - 1)vBsinφ/ε, а на 2- ой грани пластины, параллельной OYZ плоскости, образуется отрицательный связанный заряд σ_p- = ε₀(ε - 1)vBsinφ/ε, где ε₀ - электрическая постоянная.

[6] №2.416

8. С поверхности цилиндрического провода а радиуса, по которому течёт постоянный ток I силой, перпендикулярно поверхности этого провода вылетает в вакууме электрон с известным v₀ модулем скорости, вектор v₀ которого направлен по OZ оси. На какое z_max максимальное расстояние удалится электрон от OO′ оси этого провода, прежде чем повернуть обратно под действием магнитного поля тока?

Ответ:

, где μ₀ - магнитная постоянная.

[6] №2.417

9. Заряженная частица с нерелятивистским значением v модуля вектора v скорости влетает в вакууме в пространство между внутренней с a радиусом и внешней с b радиусом обкладками цилиндрического конденсатора, пролетает электрическое поле этого цилиндрического конденсатора, а затем попадает в однородное магнитное поле, вектор B индукции которого перпендикулярен вектору v скорости заряженной частицы. В однородном магнитном поле заряженная частица

двигается по круговой Т траектории с R радиусом.

Напряжение между обкладками цилиндрического конденсатора равно U. Определить модуль v вектора v скорости заряженной частицы при движении по круговой Т траектории и её q/m удельный заряд.

;

Ответ:

[6] №2.430

10. В микротроне релятивистские электроны двигаются по спиральной орбите под действием внешнего магнитного поля, имеющего вектор B индукции, перпендикулярного плоскости этой спиральной орбиты. При очередном подлёте релятивистских электронов к пластинам с внешним переменным напряжением, частота которого равна ν, полярность напряжения на этих пластинах

должна быть ускоряющей для электрона, для чего период вращения электрона на i-ой орбите делают кратным периоду переменного напряжения на пластинах. Сколько n раз релятивистскому электрону необходимо пройти вблизи ускоряющих пластин, чтобы приобрести W энергию. Ответ: n =2πνW/eBc², где e - элементарный заряд; c -скорость света в вакууме.

[6] №3.238

11. Тонкая катушка, имеющая вид кольца с R радиусом, состоит из n витков провода. Катушка находится в поле электромагнитной волны ν частоты, направление распространения которой и её E электрический вектор перпендикулярны OO′ оси катушки. Задано E_m амплитудное значение электрического вектора E электромагнитной волны. Найти амплитудное значение ЭДС индукции E_im в катушке.

Ответ: E_im =2π²R²E_mνn /eBc², где e - элементарный заряд; c -скорость света в вакууме.

[6] №3.244

12. В вакууме вдоль OY оси распространяются две плоские одинаково поляризованные электромагнитные волны, векторы E₁, E₂ напряжённости электрического поля которых

изменяются по следующим уравнениям с гармоническими функциями: E₁ = E₀cos(ωt - ky) и E₂ = E₀cos(ωt - ky + φ), где E₀ = kE₀ - вектор амплитуды каждой из плоских электромагнитных волн, а k - орт декартовой системы координат по OZ оси; φ - начальная фаза колебаний вектора E₂ напряжённости электрического электрического поля второй электромагнитной волны. Найти <S> среднее значение S модуля вектора S Пойнтинга этой электромагнитной волны.

Ответ: <S> = ε₀сE₀ ²(1+ cosφ) кг/с³ (Вт/м²), где ε₀ - электрическая постоянная.

[6] №3.245