Міністерство освіти і науки, молоді та спорту України

Київський національний університет технологій та дизайну

Методичні вказівки до лабораторних робіт з фізики

АТОМНА ФІЗИКА

(Модуль 4)

Лабораторна робота № 72

ДОСЛІДЖЕННЯ СПЕКТРА АТОМА ВОДНЮ

Затверджено на засіданні кафедри

від 31.08.2012 протокол №1

Київ-2012

Лабораторна робота № 72

ДОСЛІДЖЕННЯ СПЕКТРА АТОМА ВОДНЮ

Теоретичні відомості

Дослідження спектрів випромінювання розріджених газів і окремих атомів показали, що кожному газу властивий цілком певний, характерний тільки для нього лінійчатий спектр, який складається з окремих спектральних ліній чи груп близько розташованих ліній, кожній з яких відповідає певна частота випромінювання. Найпростішу структуру має спектр найпростішого атома - атома водню, який випромінює тільки в оптичному діапазоні (ультрафіолетова, видима та інфрачервона частина спектра електромагнітного випромінювання).

Всі спектральні лінії спектра атома водню групуються у серії. Сукупність спектральних ліній, які у своїй послідовності частот (або довжин хвиль) і в розподілі інтенсивності виявляють певну закономірність, називають спектральною серією. В межах кожної серії частоти спектральних ліній підлягають спільним на вигляд закономірностям, що свідчить про однаковий механізм випромінювання атома водню в різних областях оптичного спектра.

Перші дослідження закономірностей випромінювання атома водню у видимій частині спектра у 1885 р. зробив швейцарський вчений Й. Бальмер. Він підібрав емпіричну формулу, яка добре визначала довжини хвиль відомих на той час спектральних ліній випромінювання водню у видимій області:

, (1)

де – довжина хвилі, = 1,1 • 10^-7 м – постійна Рідберга; – цілі числа.

Врахувавши, що , де = 3 • 10⁸ м/с – швидкість світла у вакуумі, попередню формулу можна записати у вигляді:

(1*)

де величина 3,29 • 10¹⁵ с^-1 – також називається постійною Рідберга;

Спектральні лінії, які підлягають залежностям (1) і (1*), утворюють серію ліній, яка називається серією Бальмера. На нинішній час у спектрі випромінювання водню виявлено 37 ліній серії Бальмера. Зі збільшенням лінії серії зближуються; значення визначає границю серії, до якої з боку більших частот прилягає суцільний спектр: . Крім того, виявляється, що зі збільшенням номера лінії її інтенсивність зменшується. Якщо схематично зобразити розміщення спектральних ліній відповідно до формули

,

а довжиною штриха виразити інтенсивність спектральної лінії, то отримуємо картину, зображену на рис. 1.

На початку ХХ ст. у спектрі водню було виявлено ще декілька серій випромінювання, які знаходяться поза видимою областю.

В ультрафіолетовій області – серія Лаймана:

, ;

в інфрачервоній області – серія Пашена:

, ;

серія Брекета:

, ;

серія Пфунда:

, ;

серія Хемфрі:

, .

Всі серії у спектрі водню можуть бути описані однією формулою, яка називається узагальненою формулою Бальмера:

,

де число =1, 2, 3, 4, 5, 6 визначає серію, а число визначає окремі лінії кожної серії.

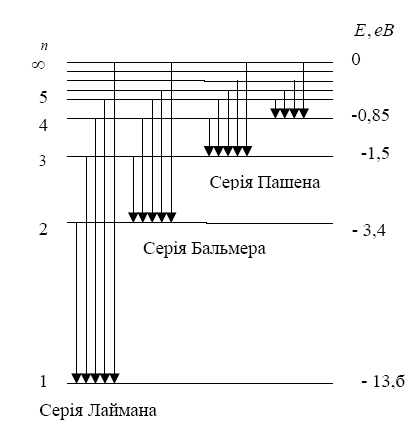
Спектральні серії водню наведені на рис. 2.

Р.Рідберг показав, що не лише в спектрі водню, але і в спектрах інших елементів, лінії утворюють закономірні серії, частоти яких можуть бути представлені у вигляді різниці двох функцій

і ,

які називаються спектральними термами, тобто

.

Для певної серії число має стале значення. Зміна числа дає всі лінії цієї серії.

Наведені серіальні формули підіб­рані емпірично і довгий час не мали теоретичного обґрунтування.

Перша спроба побудови якісно нової теорії атома була зроблена в 1913 р. данським ученим Н.Бором. Він поставив перед собою мету зв’язати в єдине ціле емпіричні закономірності лінійчатих спектрів, ядерну модель атома Резерфорда і квантовий характер випромінювання та поглинання світла.

Теорія Бора застосовна до атома водню і воднеподібних систем – іонів, які складається з ядра з зарядом і одного електрона, що обертається навколо ядра: , ,….

В основу своєї теорії Бор поклав три постулати.

Перший постулат Бора (постулат стаціонарних станів): в атомі існують певні стаціонарні стани з відповідними значеннями енергії перебуваючи в яких, атом не випромінює енергії.

Цим стаціонарним станам відповідають стаціонарні орбіти, по яких рухаються електрони, які, нез­важаючи на наявність у них прискорення, електромагнітних хвиль не випромінюють.

Другий постулат Бора (правило квантування орбіт): у стаціонарному стані атома електрон, рухаючись по коловій орбіті, має квантовані значення моменту імпульсу, які відповідають умові

, , ,

де m – маса електрона, – його швидкість, – радіус орбіти електрона, - постійна Планка, ħ= - постійна Дірака.

Третій постулат Бора (правило частот): при переході атома з одного стаціонарного стану в інший випромінюється або поглинається один квант енергії – фотон з енергією , яка дорівнює різниці енергій відповідних стаціонарних станів.

Випромінювання фотона відбувається при переході атома зі стану з більшою енергією у стан з меншою енергією , тобто при переході електрона з орбіти більш віддаленої від ядра на ближчу до ядра орбіту. Поглинання енергії супроводжується переходом атома у стан з біль­шою енергією, і електрон переходить на більш віддалену від ядра орбіту. Набір можливих частот квантових переходів і визначає лінійчатий спектр атома.

Постулати, висунуті Бором, дозволили побудувати теорію, яка дає можливість розрахувати спектр атома водню і воднеподібних систем.

Враховуючи припущення Резерфор­да, що електрон у воднеподібній системі рухається по коловій орбіті радіусом r під дією доцентрової кулонівської сили, запишемо (формула Резерфорда):

.

Звідси

.

Підставивши сюди величину з виразу , отримаємо:

і ,

де n=1, 2, 3,…

Радіуси орбіт зростають пропорційно квадратам цілих чисел.

Для атома водню (Z=1) радіус першої орбіти електрона при n=1 називається першим борівським радіусом і дорівнює

Тоді

.

Оскільки експериментально виміряти радіуси орбіт неможливо, то для пере­вірки правильності теорії потрібно знайти такі величини, які можна виміряти експериментально. Такою величиною може бути, зокрема, енергія, яку випромінюють або поглинають атоми.

Енергія електрона у воднеподібній системі дорівнює сумі його кінетичної і потенціальної енергій в електростатичному полі ядра:

.

Врахувавши, що (формула Резерфорда),

отримаємо:

-

кінетична енергія електрона на стаціонарній орбіті дорівнює половині потенціальної.

Тоді

.

Підставимо в цей вираз значення :

.

Знак „–“ означає, що електрон знаходиться у зв’язаному стані.

Енергетичні стани атома утворюють сукупність енергетичних рівнів, що змінюються залежно від значення n, яке виражає номер енергетичного рівня атома і називається головним квантовим числом. Енергетичний стан з n=1 є основним станом, а стани з n>1 – збуджені.

Надаючи n різні цілочислові значення, отримаємо для атома водню (Z=1) можливі рівні енергії (Рис. 3). Енергія атома водню зі збільшенням n зростає (зменшується її від’ємна величина), і енергетичні рівні наближаються до границі, що відповідає значенню . Атом водню має мінімальну енергію при n=1 і максимальну при . Значення відповідає енергії іонізації атома (відриву від нього електрона). Енергія іонізації з певного стану дорів­нює за абсолютною величиною енергії зв’язку електрона в атомі в цьому стані .

Згідно з третім постулатом Бора при переході електрона з n-ї орбіти на k-у випромінюється фотон з енергією

,

звідки частота випромінювання

,

де

- (2)

стала Рідберга. Значення обчислене з формули (2) добре узгоджується з експериментально отриманим в емпіричних формулах для атома водню. Це підтверджує правильність формули Бора для енергетичних рівнів воднеподібної системи.

Теорія Бора не позбавлена внутріш­ніх протиріч, тому що з одного боку, застосовує закони класичної фізики, з іншого – ґрунтується на квантових постулатах. Вона змогла пояснити спектри водню і воднеподібних систем і обчислити частоти спектральних ліній, але не змогла пояснити їх інтенсивність і не дала відповіді на запитання: чому здійснюються ті чи інші переходи? Теорія Бора не спроможна описати атом гелію – наступний за воднем атом, де на орбітах два електрони.

Для спостереження спектральних ліній і вимірювання відповідних їм довжин хвиль використовується призмовий монохроматор УМ-2 (рис. 4). Світло від досліджуваного джерела Л концентрується з допомо­гою конденсора К на щілині 1 коліматора, ширина якої регулюється мікрометричним гвинтом 9. Сфокусо­ваний з допомогою гвинта 8 коліматорним об'єктивом 2 вузький промінь напрямляється на систему скляних призм Р₁-Р₃, з допомогою яких він розкладається у спектр. Розкладене внаслідок дисперсії у призмах світло

потрапляє в зорову трубу, через окуляр 5 якої спостерігається спектр.

Рис.4.

З допомогою мікрометричного гвинта, пов'язаного з відліковим барабаном 7, можна обертати навколо вертикальної осі столик 6, на якому розташовані призми. Це потрібно для того, щоб сумістити потрібну лінію спостережуваного спектра з вістрям покажчика 10, розташованого в центрі фокальної площини об'єктива 4 зорової труби. Покажчик і суміщена з ним спектральна лінія спостерігаються через окуляр 5. Кут, на який відхиляється призмою світло певної довжини хвилі, завжди залишається сталим. Величина цього кута виз­начається кутом повороту відлікового барабана мікрогвинта 7 і вимірюється числом поділок на шкалі бараба­на.

При дослі­дженні спектру водню у роботі використо­вуються газорозрядні трубки, які для збу­дження електричного розряду підключають­ся до джерела високої напруги. Тому під час виконання роботи не можна дотикатися руками до оголених

Щоб визначити довжину хвилі спектральної лінії, потрібно спочатку проградуювати шкалу спектроме­тра, тобто установити однозначну відповідність між показами монохроматора – поділками шкали барабана і довжиною хвилі спектральної лінії, що потрапляє на покажчик об’єктива зорової труби. Для побудови такого графіка використаємо газорозрядну лампу, наповнену неоном. В лінійчатому спектрі неону довжини хвиль спект­ральних ліній добре відомі. Можна також використати відому для цього монохроматора функціональну залежність між довжиною хвилі і поділками барабана .