2.3. Технологии mimo. Пространственное мультиплексирование.

MIMO (Multiple Input – Multiple Output) - многоантенные технологии, используемые для решения двух задач:

- повышения качества связи за счет пространственного временного/частотного кодирования и (или) формирования лучей (beamforming),

- увеличения скорости передачи при использовании пространственного мультиплексирования.

В любом варианте MIMO речь идет об одновременной передаче в одном физическом канале нескольких сообщений. Для реализации MIMO используют многоантенные системы: на передающей стороне имеется M передающих антенн, а на приемной стороне N приемных. Эту структуру поясняет рис. 2.19.

Математическая модель, описывающая систему (рис.2.19), представляет собой векторное уравнение

r = H × s + n (2.5)

где r и s - вектора принятых и переданных сигналов, а n – вектор помех на входе приемников.

Рис.2.19. Модель канала с М передающими и N приемными антеннами

Коэффициенты передач между различными передающими и приемными антеннами определяет матрица H:

(2.6)

элементы которой h_ij являются комплексными коэффициентами передачи напряжения между i приемной антенной и j передающей. Для того, чтобы приемник мог различать сигналы, передаваемые разными антеннами, коэффициенты матрицы Н должны быть между собой некоррелированными.

Пространственное мультиплексирование применяют в сетях стандартов UMTS, Wi-Fi, WiMAX и LTE. При использовании пространственного мультиплексирования существенно усложняется построение приемников. Каждый независимый поток данных создает помехи другим потокам. Поэтому пространственное мультиплексирование реализуют в “хороших” каналах, с высоким отношением сигнал/помеха. Для разделения потоков в приемнике необходимо, чтобы число приемных антенн N было не меньше числа передаваемых потоков данных. Если принять, что каждый поток идет через одну передающую антенну, то в соответствии с рис.2.19 N M. Теория и практика показывают, что с увеличением числа приемных антенн (например, при N=4 и М=2 в сравнении с вариантом N=2 и М=2) коэффициент ошибок снижается. Что касается алгоритмов обработки сигналов в приемнике, то все производимые в них операции выполняют на каждой поднесущей.

Опишем различные алгоритмы обработки сигналов в приемнике при пространственном мультиплексировании.

Алгоритм максимального правдоподобия. Приемник максимального правдоподобия выполняет векторное декодирование и является оптимальным в смысле минимизации вероятности ошибки. В приемнике производят перебор всех возможных вариантов переданного вектора s. При равной вероятности передачи любых вариантов s искомым сигналом считают , минимизирующий оценку:

(2.10)

Прямая реализация алгоритма при двух независимых потоках и модуляции 16-КАМ требует перебора 16² возможных состояний сигнала, при 4 потоках ‒ 16⁴, а при модуляции 64-КАМ 64⁴ состояний. Просмотр такого числа вариантов пока практически нереализуем, хотя методы сферического декодирования, требующие дополнительного совместного исследования матрицы Н и помех, позволяют существенно уменьшить зону поиска.

Линейные алгоритмы.

Линейные алгоритмы основаны на решении системы М линейных уравнений, получаемых путем псевдообращения матрицы коэффициентов Н (2.4). Этот алгоритм принято называть ZF (Zero-Forcing). Если матрица Н квадратная, то-есть, число независимых потоков данных М равно числу приемных антенн N, то вектор переданных сигналов s можно определить, умножив левую и правую части (2.5) на обратную матрицу H^-1 и решив следующую систему уравнений:

s = H^-1 × r – H^-1 × n (2.11)

Если число приемных антенн N больше числа принимаемых потоков данных М, то матрица Н становится прямоугольной размерностью N×М (Н_NM). В этом случае выполняют псевдообращение матрицы Н^MP по алгоритму Мура-Пенроуза, где используют матрицу Н^Н, эрмитово-сопряженную с матрицей Н. Матрицу Н^Н получают, транспонируя матрицу Н и заменяя все элементы h_ij на их комплексно-сопряженные значения. Оператор

(2.12)

имеет размерность М×N. Заменив в (2.11) H^-1 на Н^MP, получаем

s = Н^MP × r – Н^MP × n (2.13)

Оба варианта ZF-приемника (2.11) и (2.13) отличаются вычислительной простотой, но дают существенно худший результат в сравнении с алгоритмом максимального правдоподобия, поскольку после умножения Н^MP × n усиливается влияние помех.

С целью улучшения приема используют модифицированный ZF-алгоритм, получивший название MMSE (Minimum Mean Square Error). В MMSE-приемнике оператор Н^MP заменен оператором W_MMSE:

(2.14)

где - соотношение сигнал/помеха, а – единичная матрица размерности M.

Нелинейные алгоритмы.

Нелинейные алгоритмы приемников сигналов с пространственным мультиплексированием дают лучшие результаты, чем линейные, но требуют значительно бόльшего объема вычислений. Одним из наиболее известных нелинейных алгоритмов является Vertical-Bell Labs Layered Space Time Architecture или V-BLAST. Алгоритм работы V-BLAST включает в себя как линейные, так и нелинейные операции. Он основан на QR-разложении канальной матрицы H_NM с последующим определением и исключением отдельных принятых символов. Матрицу H_NM представляют в виде произведения

Н_NM = Q_NM R_MM (2.15)

где Q_NM – унитарная матрица, удовлетворяющая условию:

,

а R_MM – диагональная матрица вида

(2.16)

Далее преобразовываем уравнение (2.5), умножая его левую и правую части на , к виду

, (2.17)

где вектор , а вектор . Отметим, что вследствие унитарности матрицы мощность помех не возрастает. В результате получаем систему уравнений

(2.18)

которую решаем, находя компоненты вектора s, начиная с последнего s_M.

Результаты компьютерного моделирования работы детектора V-BLAST в зависимости от отношения сигнал/суммарная помеха (SNR) приведены на рис.2.20. Смоделирована передача 2 потоков данных с модуляцией 16-КАМ при приеме на 2 антенны.

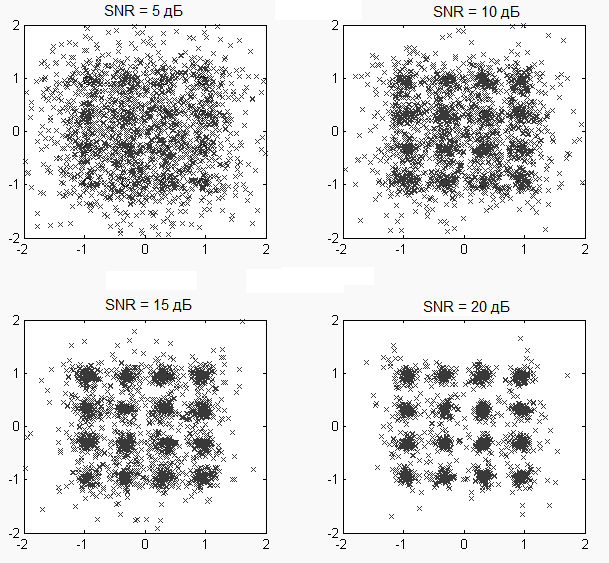
Рис. 2.20. Прием сигналов при пространственном мультиплексировании