Міністерство освіти і науки, молоді та спорту україни

Національний університет “Львівська політехніка”

Кафедра телекомунікацій

ЗАВДАННЯ ДО ПРАКТИЧНОЇ РОБОТИ № 3

«Багатокритерійна задача пакування рюкзака»

І МЕТОДИЧНІ ВКАЗІВКИ ДО ЇХ ВИКОНАННЯ

З курсу “Основи теорії систем”

для студентів базового напряму 6.0924 “Телекомунікації”

Львів 2012

Завдання до практичної роботи №3 «Багатокритерійна задача пакування рюкзака» і методичні вказівки до їх виконання з курсу “Основи теорії систем” для студентів базового напряму 6.0924 “Телекомунікації”. – Львів – 2012. – 6 стор.

Автори: к.т.н., ст. викл. Демидов І.В.

к.т.н., асистент Юркевич О.В.

Рецензенти: д.т.н., професор Русин Б.П.

д.т.н., професор Климаш М.М.

В завданні до практикуму з курсу “Основи теорії систем” і методичних вказівках до його виконання розглянуто основні методи розв’язання комбінаторної задачі пакування рюкзака.

Завдання до практикуму і методичні вказівки до їх виконання затверджено на засіданні кафедри “Телекомунікації” Національного університету “Львівська політехніка” 27.08.2004 р., протокол № 1.

Тема заняття: Багатокритерійна задача пакування рюкзака.

Мета роботи: навчитися виконувати оптимізацію при утворенні систем з набору компонентів.

Задача пакування рюкзака є задачею комбінаторної оптимізації. Вона полягає у наповнені рюкзака, що здатен витримати деяку максимальну масу, предметами, кожен з яких має вартість (або корисність) та масу. Необхідно обрати об'єкти в такий спосіб, аби максимізувати сумарну вартість (або користь), але не перевищити максимально припустиму масу.

Існуючі алгоритми, на практиці, здатні розв'язати задачі досить великих розмірів. Однак, унікальна структура задачі, а також той факт, що вона присутня як підзадача у більших, загальніших проблемах, робить її важливою для наукових досліджень.

Дана задача використовується для моделювання різних проблем, зокрема:

• При складанні телекомунікаційних систем обмежених за масою/вартістю: задачі проектування штучних супутників землі, переносних терміналів зв’язку та інші.

• В системах підтримки управління портфелем для балансування та диверсифікації вибраних капіталовкладень з метою пошуку найкращого балансу між ризиками та ефективністю вкладів у різні фінансові активи;

• При завантаженні човна або літака: вибір багажів для оптимального завантаження транспортного зособу;

• В розкроюванні різних матеріалів (тканини, сталеві листи, тощо): вибір оптимальної схеми розкрою матеріалів з метою зменшення кількості відходів.

Постановка задачі

Задачу пакування рюкзака можна визначити засобами математичного апарату. Нехай кожному об'єктові для пакування співставлено індекс i, який приймає значення від 1 до n. Числа w_i та p_i відповідають масі та вартості об'єкта i. Максимальна припустима маса, яку здатен витримати рюкзак, дорівнює W.

Існує багато варіантів заповнення рюкзака. Для описання окремого варіанту пакування необхідно вказати для кожного об'єкта, чи його обрано (запаковано). Для цього можна використати двійковий вектор , компонента x_i якого дорівнюватиме 1, якщо i-тий об'єкт запаковано, та 0 якщо ні. Цей вектор називається вектором заповнення. Вагу та вартість запакованих предметів, можна обчислити як фукнцію від вектора заповення. Для заданого вектора заповнення X вартість предметів запакованих в рюкзак дорівнює:

(1)

Функція z(X) називається цільовою функцією. Аналогічно, загальна маса предметів дорівнює:

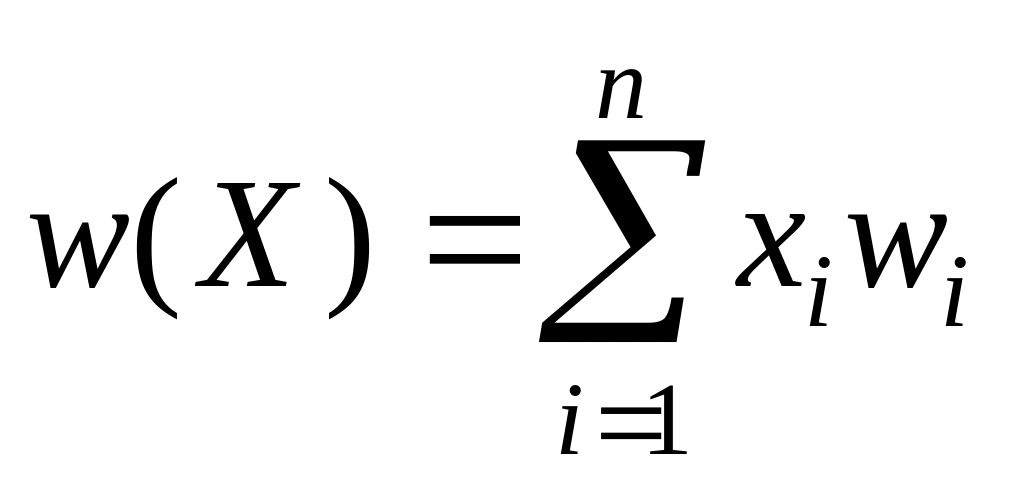(2)

Таким чином, задача пакування рюкзака полягає у відшуканні такого вектора заповення , що максимізує функцію z(X) за умови:

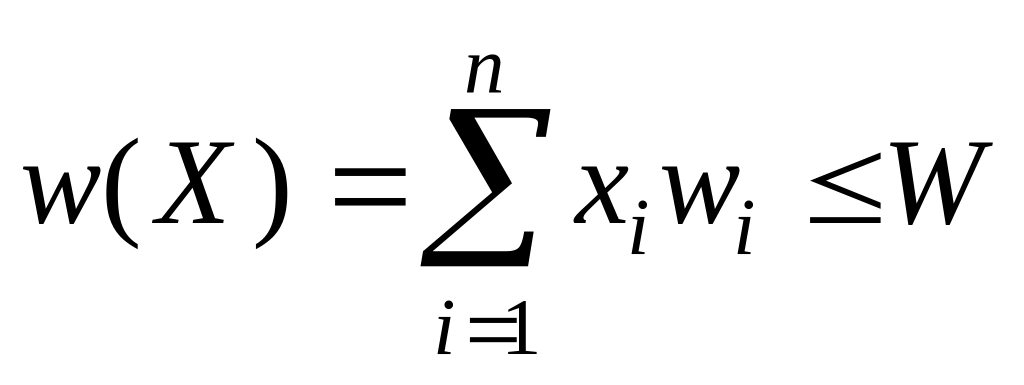(3)

Тобто, загальна маса обраних предметів w(X) не перевищує можливості рюкзака W. Будь-який вектор X, що відповідає умові (3) називається припустимим. Якщо вартість z(X) максимальна, то вектор X називається оптимальним.

Додаткові умови задачі:

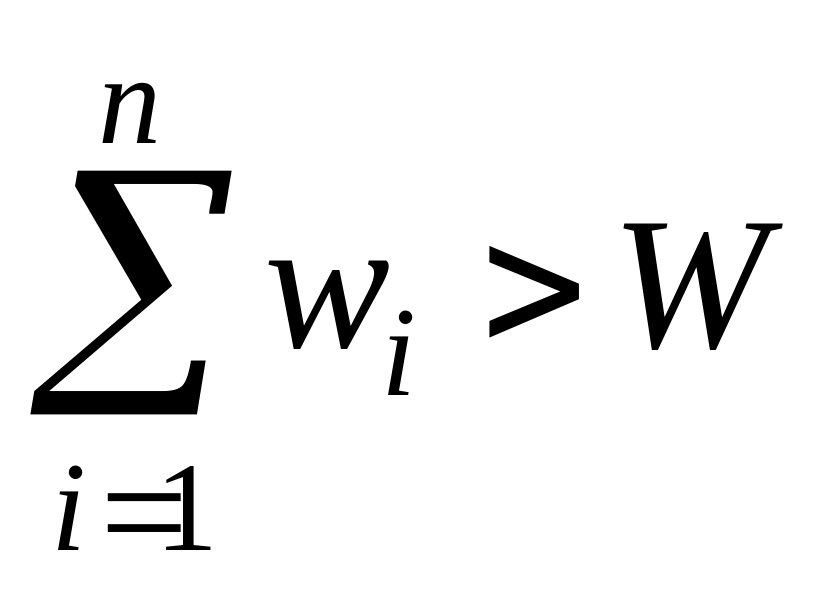• : всі доступні об'єкти не можливо покласти до рюкзака разом;

• p_i > 0, i  {1, … , n} : будь-який додатковий об'єкт надає перевагу;

• w_i > 0, i  {1, … , n} : будь-який об'єкт використовує ресурси.

Така задача називається «0-1 Задачею пакування рюкзака». Якщо окрім вартості предмети мають ще одну характеристику (наприклад, щільність), то задача пошуку вектора заповнення X, що максимізує обидві функції (сумарна вартість та сумарна щільність) є багатокритеріальним варіантом «0-1 Задачі пакування рюкзака».[1]