Уравнение Бернулли.

Уравнением Бернулли называется уравнение вида

при n ≠ 0, n ≠ 1. (13)

При n = 0 уравнение (13) линейное, при n = 1 – уравнение с разделяющимися переменными.

Чтобы решить уравнение Бернулли, надо обе его части разделить на уⁿ, полагая, что у ≠ 0 (функция у = 0 также удовлетворяет уравнению), и cделать замену . Тогда и получим: – линейное уравнение, которое можно решать любым изложенным выше методом.

Замечание 1.Уравнение Бернулли можно решать, не приводя к линейному уравнению. Общее решение уравнения (13) представим в виде произведения двух неизвестных функций y = u·v и выполним все необходимые действия (метод введения произвольных функций (метод Эйлера)).

1. Дифференциальные уравнения n-го порядка. Основные понятия и определения. Задача Коши. Теорема существования и единственности.

Геометрическое и механическое истолкование уравнения второго порядка и его решения.

Рассмотрим более подробно вопрос, о геометрическом истолковании уравнения второго порядка и его решения.

Уравнение второго порядка имеет общий вид

(1)

Его всегда можно переписать так:

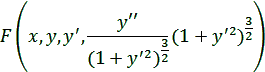(2)

Так как кривизна кривой y = y(x) в точке (x, y), то из формулы (2) видно, что всякое дифференциальное уравнение второго порядка выражает некоторое общее свойство его интегральных кривых y = y(x), устанавливая в каждой точке интегральной кривой зависимость между координатами точки, наклоном касательной к интегральной кривой и кривизной интегральной кривой в этой точке.

Рассмотрим теперь вопрос о механическом истолковании уравнения второго порядка и его решений. Пусть материальная точка массой m движется по прямой, которую примем за ось x, под действием силы F (t, x, ), зависящей от времени t, положения x и скорости в момент времени t. Тогда согласно второму закону Ньютона имеем

(3)

где есть ускорение точки в момент времени t. Перепишем уравнение (3) в виде

(4)

где f =

Всякому решению

x = x(t) (5)

соответствует, как и в случае уравнения первого порядка, определенный закон движения. Поэтому часто решение (5) называют движением, определяемым уравнением (5). Задача, теории интегрирования уравнения (4) состоит в нахождении всех движений, определяемых этим уравнением, и изучении их свойств. Так как уравнение (4) удается проинтегрировать в конечном виде лишь в редких случаях, то весьма важно уметь устанавливать свойства движений, определяемых этим дифференциальным уравнением непосредственно по свойствам самого дифференциального уравнения.

Постановка задачи Коши для уравнения n-го порядка

Для уравнения n-го порядка

(6)

(n > 1) задача Коши ставится так: найти решение

y = y(x) (7)

удовлетворяющее начальным условиям (условиям Коши)

(8) где — заданные числа (начальные данные решения (7). В отличие от уравнения первого порядка здесь при заданном значении независимой переменной задается значение не только искомой функции, но и ее производных до порядка на единицу ниже, чем порядок дифференциального уравнения.

В частности, для уравнения второго порядка (1) начальные условия (8) принимают вид

y = y₀, y ' = при x = x₀.

Геометрически речь идет о нахождении интегральной кривой y = y(x), проходящей через заданную точку M₀ (x₀, y₀) и имеющей в этой точке касательную M₀T, которая образует с положительным направлением оси x заданный угол α₀:

tg α₀ = .

Наряду с задачей Коши большое значение имеет задача, в которой условия на искомую функцию (и ее производные) налагаются не к одной точке, а на концах некоторого промежутка. Такая задача называется краевой задачей, а налагаемые условия — краевыми условиями.

Теорема существования и единственности решения уравнения n-го порядка

Рассмотрим уравнение n-го порядка в нормальной форме

y⁽ⁿ⁾ = f (x, y, y ', …, y ^(n-1)). (9)

Для этого уравнения, как и в случае уравнения первого порядка, имеет место следующая теорема существования и единственности решения задачи Коши.

Теорема Пикара. Если правая часть уравнения (9) непрерывна в некоторой окрестности начальной точки ( ) и имеет непрерывные в этой окрестности частные производные по y, y ', …, y^(n-1) то оно имеет единственное решение (7), удовлетворяющее начальным условиям (8).

Случай линейного уравнения. Выбор начальных данных. Интервал существования решения.

Рассмотрим линейное уравнение n-го порядка

(10)

Предположим, что все коэффициенты p₁, …, p_n и правая часть f (x) заданы и непрерывны в интервале (a, b). Тогда условия сформулированной выше теоремы Пикара заведомо выполняются в окрестности начальной точки ( ), где , - любые заданные числа. Поэтому для линейного уравнения (10) имеет место следующая теорема существования и единственности решения задачи Коши.

Теорема. Если функции p₁, …, p_n, f (x) непрерывны в интервале (a, b), то уравнение (10) имеет единственное решение (7), удовлетворяющее начальным условиям (8), причем можно задавать произвольно, а x₀ можно брать любым из интервала (a, b).

Можно доказать, что решение (7) определено во всем интервале (а,b).

В частности, если функции p₁, …, p_n ,f (x) — полиномы (или другие функции, непрерывные при всех x), то все начальные данные можно задавать произвольно. Решение существует, единственно и определено при всех x.

Если функции p₁, …, p_n, f (x) суть рациональные функции, т. е. являются отношениями полиномов

(11)

то при постановке задачи Коши начальные значения можно задавать любыми, а можно брать любым, кроме действительных нулей знаменателей Q₁, …, Q_n, Q_n+1. Решение с такими начальными данными будет заведомо определено в окрестности точки x₀, не содержащей нулей знаменателей Q₁, …, Q_n, Q_n+1.