1. Дифференциальные уравнения 1-го порядка. Основные понятия и определения. Задача Коши. Теорема существования и единственности решения.

Дифференциальным уравнением 1-го порядка называется уравнения вида , где х – независимая переменная, у(х) – неизвестная функция. В форме, разрешенной относительно производной, уравнения первого порядка записывается так: .

Функция y = y(x) называется решением дифференциального уравнения F(x, y, y ') = 0, если она непрерывно дифференцируема на (a,b) и F(x, y(x), y '(x)) ≡ 0 для всех x из (a,b) .

График решения дифференциального уравнения называют интегральной кривой дифференциального уравнения.

Дифференциальное уравнение 1–го порядка имеет бесконечно много решений. Для того чтобы выделить единственное решение, нужно задать дополнительные (начальные) условия.

Задача отыскания решения y = y(x) уравнения F(x, y, y') = 0 , удовлетворяющего условию y(x₀) = y₀, называется задачей Коши (или начальной задачей).

Условие y(x₀) = y₀ — начальное условие.

Любое конкретное решение y = y(x) (решение задачи Коши) уравнения 1–го порядка, называется частным решением уравнения.

Общее решение уравнения, записанное в неявной форме Φ(x, y) = C, называется общим интегралом уравнения.

Частное решение уравнения, записанное в неявной форме Φ(x, y) = 0, называется частным интегралом уравнения.

Уравнение 1-го порядка, разрешенное относительно производной, называют уравнением, записанными в нормальной форме:

Уравнения первого порядка часто записывают в дифференциальной форме:

M(x, y)dx + N(x, y)dy = 0.

Решение такого уравнения можно искать как в виде y = y(x) , так и в виде x = x(y) .

Теорема существования и единственности решения

Теорема.

Пусть (1)

дифференциальное уравнение. Будем предполагать, что задана на некотором открытом множестве , которое принадлежит плоскости (декартовых координат). Предположим, что и непрерывны на .

Тогда:

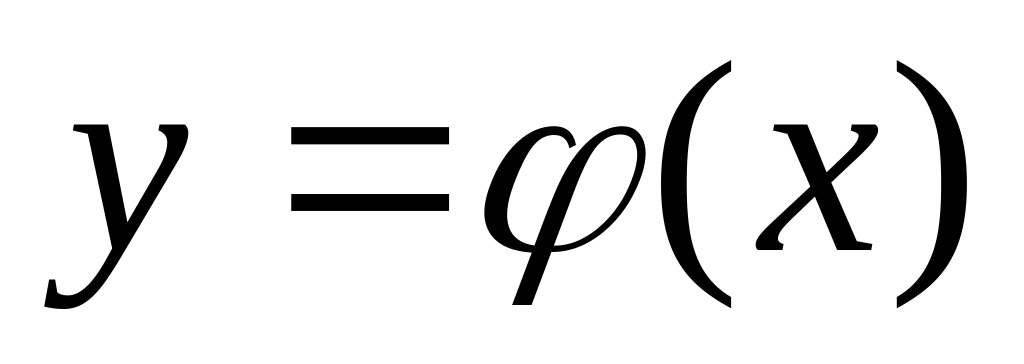1. Для любой точки найдется решение уравнения (1), которое удовлетворяет условию 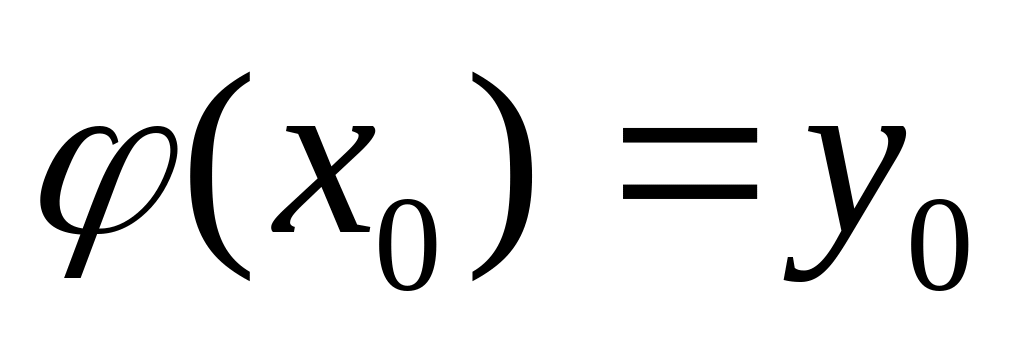(2)

2. Если два решения 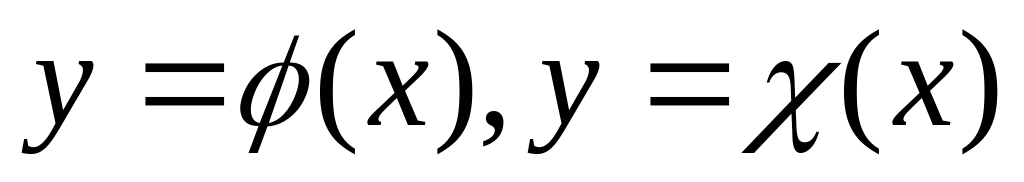уравнения (1) совпадают хотя бы в одной точке , то решение и будут тождественно равны для всех значений переменной , для которых они определены.

2. Основные типы дифференциальных уравнений 1-го порядка и методы их решения (с разделяющими переменными, однородные и приводящие к однородным, линейные уравнения и приводящиеся к линейным).

Дифференциальные уравнения с разделяющимися переменными это уравнения вида , (1)

где каждый из коэффициентов при дифференциалах представляет собой произведение двух функций, одна из которых зависит только от х, а вторая от у.

Уравнение может быть задано также в виде

. (2)

Следовательно, чтобы выяснить, будет ли уравнение или уравнением с разделяющимися переменными, достаточно проверить, представимы ли коэффициенты X и Y или f(x, y) в виде произведения двух функций f(x)·φ(y).

Чтобы проинтегрировать уравнение (1), нужно добиться того, чтобы коэффициент при dx зависел только от х, коэффициент при dу – только от у. Этого достигаем делением всего уравнения на произведение , полагая при этом, что . После деления уравнения (1) на получим 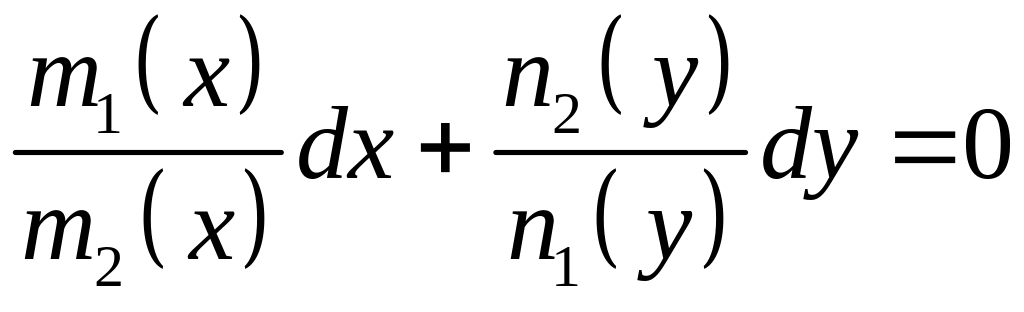. Интегрируем последнее равенство . В левой части получаем некоторую функцию Φ(х, у). Таким образом, Φ(х, у) = С – есть общий интеграл уравнения (1).

Если , то прямая у = у₀ также является интегральной прямой. Если , то можно считать и прямую х = х₀ также интегральной.

Для интегрирования уравнения (2) нужно его разделить на и умножить на dx: . При этом полагаем, что ≠ 0. Интегрируя последнее равенство, получим общее решение: .

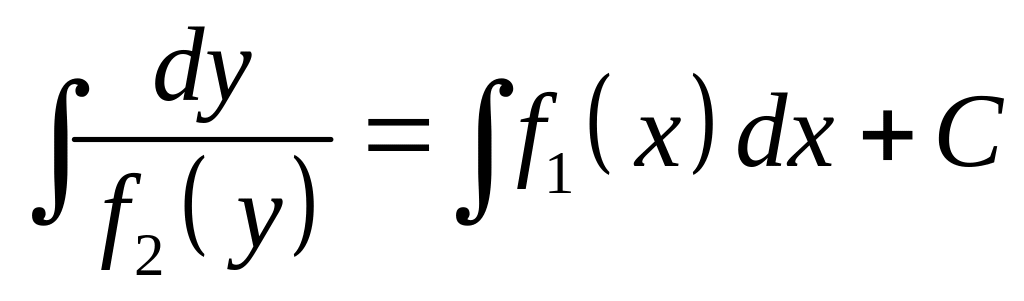Здесь, если = 0, то у = у₀ будет также решением уравнения (2).