Правила построения сетевых графиков

1. Всякая работа на сетевом графике кодируется шифрами ее конечного и начального события (i;j).

2. На сетевом графике не должно быть так называемых тупиковых событий, т.е. событий из которых не выходит ни одной работы, кроме завершающей.

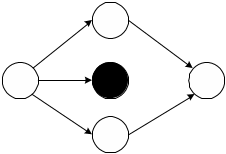
Наличие тупиков указывает на то, что это либо ошибка, либо что результат предшествующих работ ни кому не нужен.

3. Не должно быть ни одного события, за исключением исходного, в которые не входит ни одной работы.

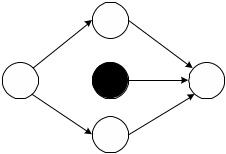
Наличие таковых событий свидетельствует либо об ошибке, либо о том, что результат необходимый одному из исполнителей, как исходное условие для начала выполнения работы ни кому не задан, а значит, данное событие не может наступить.

4. В сети не должно быть замкнутых контуров, т. е. путей соединяющие некое событие с ним же самим.

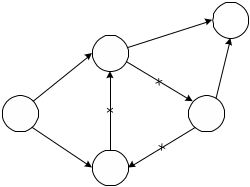
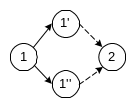
5. Если какие либо сложные работы в сети могут быть начаты до полного окончания непосредственно предшествующих им работ, то эта последняя работа может быть представлена как сумма таких последовательно выполняемых работ, результаты которых необходимы и достаточны для начала следующих за ними работ.

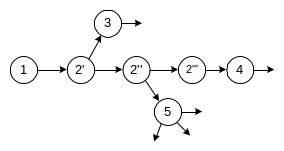
6. Нельзя допускать работы с общим начальным и конечным событием.

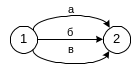
7. При выполнении параллельных работ (а, б, в), выходящих из одного предшествующего события (1) и входящих в одно последующие событие, в график вводится дополнительное событие и фиктивные работы.

Установление продолжительности работ

По каждой работе сетевого графика ответственный исполнитель определяет время ее выполнения. При этом для работ выполнявшихся, встречавшихся ранее, по которым имеются статистические данные или разработанные нормативы, устанавливается наиболее вероятная или нормативная продолжительность работ. Однако на практике, исполнитель не всегда может дать однозначную оценку времени. В таких случаях, в зависимости от принятой системы оценки, используются либо 2 оценки (t_min, t_max), либо 3 (t_min, t_max, t_н.в). Н.В. – наиболее вероятное. В этих случаях ожидаемая продолжительность работ, а следовательно и наступление событий, рассматриваются как случайные величины. Принятые для оценки значения работ являются исходными для расчета продолжительности работ.

(t_min, t_max)

(t_min, t_Н.В.,t_max)

Расчет параметров сетевого графика

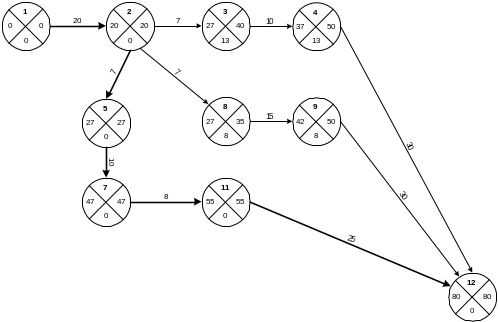
В сетевом графике рассчитываются следующие параметры:

• резервы времени событий

• резервы времени работ

• продолжительность полных путей

• критический путь

Резервы времени рассчитываются в тех случаях, когда существует более одного пути различной продолжительности.

Резерв времени события – это такой промежуток времени, на который может быть отсрочено наступления данного события, без нарушения исполнения выполнения всего комплекса работ

R_i=Тп_i-Тр_i

T_n(p)- поздний (ранний) срок совершения события, превышение которого вызовет аналогичное задержание завершающегося события.

Тп_i=Т(Lкр)-Т(L_maxic)

Иногда расчет T_n ведут по упрощенной форме:

Тп_i=(Тп_j-t_ij)min

Тр_i=Т(L_Ji)max

Тр_j=(Тр_i+t_ij)max

Для событий, принадлежащих критическому пути, резервы времени равны нулю.

Для работ сетевого графика просчитывается полный резерв времени работы и свободный резерв времени работы.

R_ijⁿ=Тп_j-Тр_i-t_ij

Полный резерв времени работы – это максимальное количество времени, на которое можно увеличить продолжительность данной работы или отсрочить ее начало, не изменяя при этом продолжительности критического пути. При этом, если полный резерв времени использовать частично или целиком для увеличения длительности какой- либо работы, то соответственно уменьшится резерв времени всех остальных работ лежащих на этом пути.

R_ij^C=Тр_j-Тр_i-t_ij

Свободный резерв времени работы – это максимальное количество времени, на которое можно увеличить продолжительность данной работы или отсрочить ее начало, не изменяя при этом ранних сроков начала последующих работ, при условии, что начальные события данной работы наступят в свой ранний срок. Этот резерв является независимым резервом, принадлежит только данной работе и его использование для данной работы не изменяет свободных ресурсов тех путей, которым принадлежит данная работа.

Для работ сетевого графика рассчитывают также ранние и поздние сроки ее начала и окончания.

Трн_ij=Тр_i

Тпн_ij=Тп_j-t_ij

Тро_ij=Тр_j+t_ij

Тпо_ij=Тп_j

При построении и расчете сетевого графика возможно 3 случая:

1. Тд<Ткр

Сетевой график – неприемлемый. Необходимо перепланировать комплекс работ до достижения условия:

Т_дТ_кр

2. Т_д=Т_кр

Сетевой график – приведенный. Необходимо сокращение стоимости работ.

3. Т_д>Ткр

Сетевой график – приемлемый. Возможен дальнейший анализ и оптимизация комплекса работ по стоимости.

Расчет вероятности Р_к наступления завершающего события в заданный срок совершенно необходим, когда директивный срок Т_д оказывается меньше наступления срока завершающего события.

Т_д<T_c (T_c=Ткр)

Предполагая, что значение Т_с подчиняется закону нормативного распределения, эту вероятность рассчитывают:

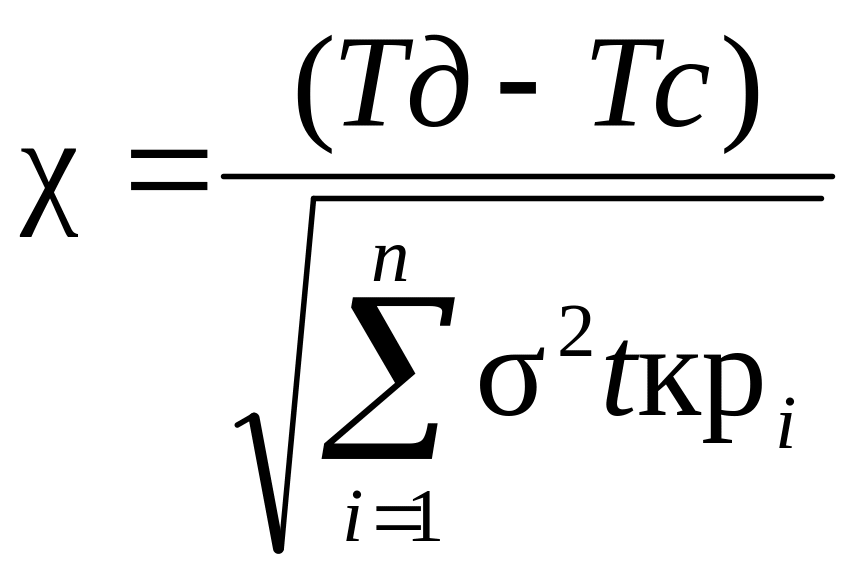
– среднеквадратическое отклонение работ, лежащих на критическом пути

По аргументу функции Лапласа находят вероятность наступления Р_к:

если Р_к>0.65, то можно утверждать, что на работах критического пути имеются избыточные ресурсы и общая продолжительность этих работ может быть сокращена.

Если Р_к<0,35, то возникает опасность срыва рассчитанного срока наступления события и она настолько велика, что необходимо повторное планирование с перераспределением ресурсов, т. е. оптимизация сетевого графика.