Матрица перемещения.

Для распространения лучей, проходящих слева направо путь t между двумя опорными плоскостями, можно записать:

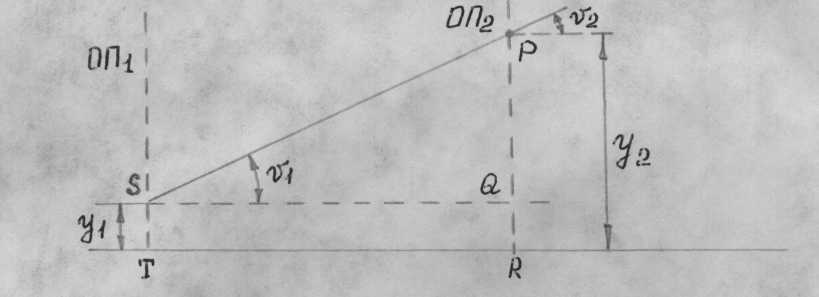
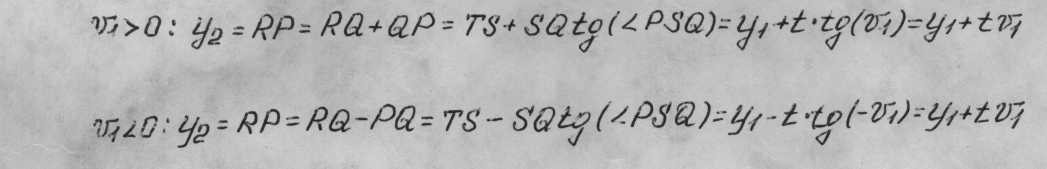
Матрица перемещения предназначена для операций с такими параметрами луча, как высота луча и оптический направляющий косинус, а не просто его угол. Таким образом, если n - пока­затель преломления среды между ОП₁ и OП₂, то приведенное выше уравнение нужно переписать в виде

где Т = t/n - приведенная толщина оптического промежутка. Нет­рудно заметить, что “V₁” и “V₂” равны друг другу. Следовательно, для нового оптического направляющего косинуса можно написать уравнение

Полученные два уравнения теперь можно записать в матрич­ной форме:

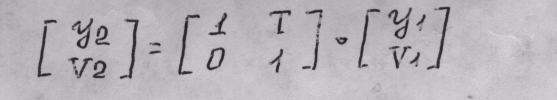
Таким образом, перемещение луча вправо описывается матрицей

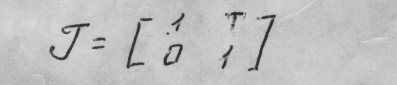
Матрица преломления.

Рассмотрим, как действует на распространение лучей кривая поверхность, разделяющая две области с показателями преломления n₁ и n₂. Радиус кривизны поверхности считается поло­жительным, когда центр кривизны расположен справа от поверхности.

На рисунке приведена поверхность положительной кривизны:

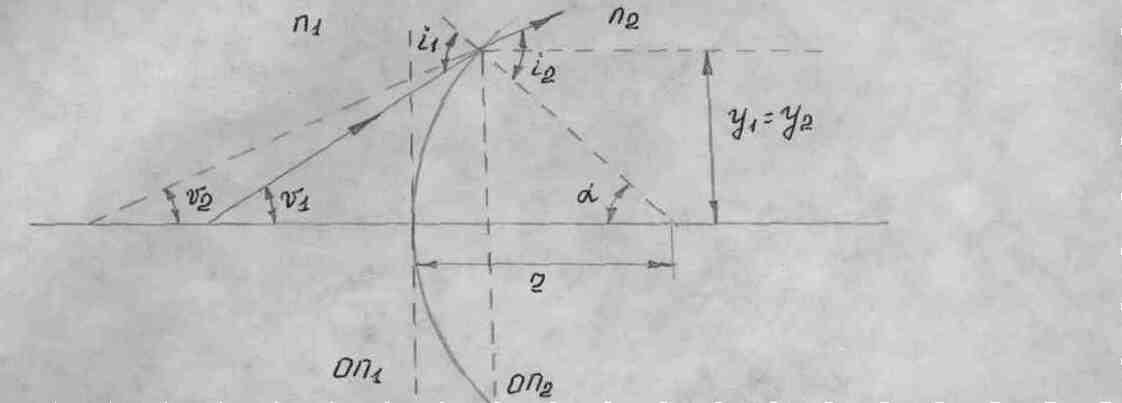
В случае параксиальных лучей расстояние между плоскостя­ми ОП₁, ОП₂ пренебрежимо мало. Отсюда имеем y₂ = y₁. Применяя закон Снеллиуса можно написать

n₁ Sin i₁ = n₂ Sin i₂

или в параксиальном приближении

n₁ i₁ = n₂ i₂

По теореме о внешнем угле треугольника

i₁ = V₁ +  = V₁ + y₁/r

i₂ = V₂ +  = V₂ + y₁/r

Следовательно

n₁(V₁ + y₁/r) = n₂(V₂ + y₁/r)

или

V₁ + n₁.y₁/r = V₂ + n₂ .y₁/r

Таким образом, переписывая эти уравнения в матричной форме, окончательно получаем

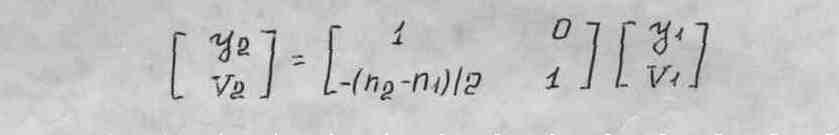
Величину (n₂ – n₁)/r обычно называют оптической силой поверхности Ф.

Получили матрицу преломления:

РАСЧЕТ ПАРАМЕТРОВ ВЫХОДНОГО ЛУЧА ПО ЗАДАННЫМ ПАРАМЕТРАМ ВХОДНОГО ЛУЧА

Если обозначить вектор луча , проходящего через r-ую опорную плоскость, как К_r, то для преобразования параметров луча из ОП_r в ОП_(r+1) можно написать следующее рекуррентное соотношение:

К_(r+1) = M_r К_r;

аналогично

К_r = M_(r-1).К_(r-1)

и так далее.

Используя повторно это рекуррентное соотношение, а также ассоциативное свойство умножения матриц, находим

K_(2n+2) = M_(2n+1) K_(2n+1) = M_(2n+1) (M_2n K_2n) = (M_(2n+1) M_2n)( M_(2n-1) K_(2n-1)) =

= (M_(2n+1) M_2n M_(2n-1) M_(2n-2)…M₃M₂M₁)K_1.

Следовательно, K_(2n+2) = MK₁, где М представляет со­бой произведение всех матриц, взятых в нисходящем порядке но­меров.

Используем теперь R-матрицу для описания действия отражающих поверхностей.

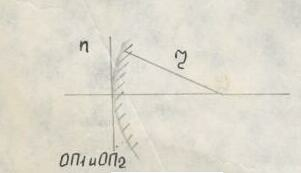
Чтобы вычислить оптическую силу Ф отражающей кривой поверхности, преоб­разуем формулу P = (n₂ – n₁)/2, заме­нив в ней показатель преломления n₂ второй среды на отрицательное значение показателя преломления n той же среды, в которую погру­жен отражатель и в которой распространяется луч после своего отражения. Таким образом получим Р = - 2n/r и R - матрица запишется в виде

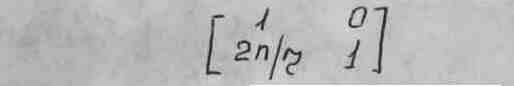
В результате всех вычислений должны получить результирую­щую матрицу, вида

Элементы А_p, В_p, С_p, D_p матрицы имеют вполне опреде­ленный смысл. Их значения характеризуют свойства системы. Для уяснения смысла коэффициентов матрицы преобразования лучей оптической системой можно поступить следующим образом: предположить, что коэффициенты равны нулю и выяснить, к чему это приведет.

Это значит, что все лучи идущие из одной и той же вход­ной опорной плоскости ОП₁, выходят из выходной опорной плоскос­ти под одним и тем же углом V₂ = C_p y₁ к оси системы (т.е. в виде параллельного пучка) независимо от того, под каким углом V₁ эти лучи входили в систему. Отсюда следует, что вход­ная плоскость ОП₁ должна быть передней фокальной плоскостью системы.

2. В_p = 0, тогда y₂ = A_p y₁ + 0V₁ = A_p y₁. Это означает, что все лучи проходящие через точку О₁(с координатой y₁) плоскости ОП₁ пройдут через одну и ту же точку О₂ (с координа­той y₂) плоскости ОП₂. Следовательно, точки О₁ и О₂ являют­ся соответственно точкой-предметом и точкой- изображением плоскостей ОП₁ и ОП₂.

3. С_p = 0, тогда V₂ = D_p V₁. Это означает, что парал­лельный пучок лучей, вошедших в оптическую систему, выйдет из нее также в вице параллельного пучка, т.е. данная оптическая система является афокальной.

4. А_p = 0, тогда y₂ = B_p V₁. Это значит, что лучи, входя­щие в систему в виде параллельного пучка лучей, в выходной плоскости ОП₂ пройдут через одну и ту же точку. Следовательно, в этом случае плоскость ОП₂ является задней фокальной плоскос­тью оптической системы.

При расчетах чаще всего используют "приведенные значе­ния" (в отношении к показателю преломляющей среды). Использо­вание приведенных значений дает следующее преимущество: при пересечении плоской границы раздела двух сред приведенные зна­чения не изменяются.