§6. Приложения определённого интеграла в механике и физике.

35.Длина пути. Пусть точка движется по прямой со скоростью v=v(t). Путь пройденный точкой от момента времени t₁ до момента t₂, выражается интегралом

S=.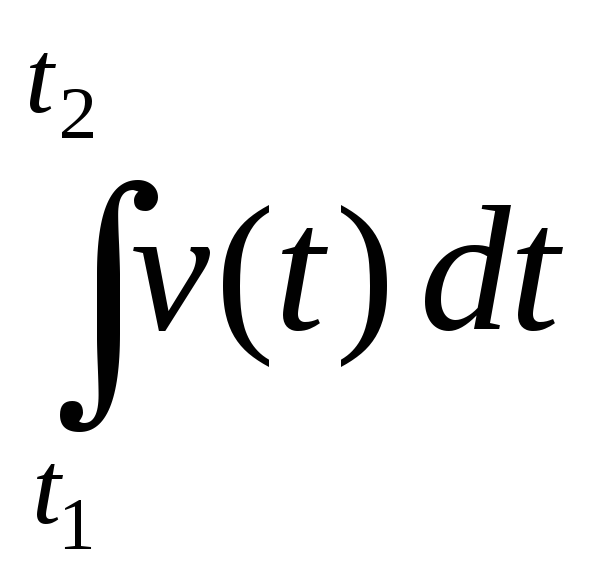

Отметим, что так как точка движется по числовой прямой, то если движение происходит в отрицательном направлении по оси (v(t)<0), то путь может получиться отрицательной величиной.

6.1. Скорость движения точки даётся формулой

v = (3t²-2 t)

найти путь, пройденный точкой за первые 4 сек от начала движения.

Решение. Вычисляем по формуле

S===64-16=48 м.

36. Давление жидкости. Для вычисления силы давления жидкости используют закон Паскаля, согласно которому сила давления жидкости на площадку S с глубиной погружения h равна

P = γ h S,

где γ - удельный вес жидкости.

6.2. Найти давление бензина, находящегося в цилиндрическом баке высотою h =3,5 м и радиусом r =1,5 м, на его стенки, если удельный вес γ = 900 .

Решение. Расположим систему координат так, как показано на рисунке. Ось симметрии цилиндра приходит по оси Oz, верхняя «крышка» цилиндра находится на плоскости xOy. Разобьём отрезок [0;3,5] на оси Oz на n частей произвольным образом: 0< z₁< z₂<…< z_n=3,5.

Вычислим площадь полоски между плоскостями z = z_i-1 и z = z_i : ∆ S_i = 2π ∙ 1,5 ∙ ∆ z_i, где ∆ z_i = z_i - z_i-1. Тогда давление жидкости на стенки полоски будет равно

∆ P_i = γ h S  900∙ z_i ∆ S_i = 900∙3 π ∆ z_i

тогда

P ==1350 π z²=16537,5 π кг  16,5 π т.

37. Работа силы. Если непрерывная переменная сила F(x) действует в направлении оси Ox, то работа силы на отрезке [x₁, x₂] выражается интегралом

A=.

6.3. Найти работу, затраченную на выкачивание воды из корыта, имеющего форму полуцилиндра, длина которого a, радиус r.

Решение. Расположим систему координат так, как показано на рис. Отрезок [0; r] по оси Oz разобьём на n частей: 0< z₁< z₂<…< z_n= r. Вычислим объём части полуцилиндра, заключённой между плоскостями z = z_i-1 и z = z_i. С точностью до бесконечно малых, которыми можно пренебречь, можно считать этот слой прямоугольным параллелепипедом высотой ∆ z_i = z_i - z_i-1 и шириной и длиной a. Тогда ∆ v_i = ∆ z_i. Удельный вес воды будем считать равным единице. Элементарная работа, совершаемая для поднятия слоя воды между плоскостями z = z_i-1 и z = z_i, на высоту z_i, равна

A_i =.

Следовательно,

A===.

6.4. Какую работу нужно затратить, чтобы растянуть пружину на 6см, если сила в 10 н растягивает её на 1см.

Решение. Согласно закону Гука сила F н, растягивающая пружину на x м, равна

F = kx,

где k - коэффициент пропорциональности. Коэффициент k найдём из условия: при x =0,01 м F =10 н. Следовательно, k ==1000, и F(x) =1000 x. Тогда

A===1,8 дж.

38. Статические моменты и центр тяжести плоской фигуры.

Пусть фигура на плоскости xOy ограничена кривыми y =  (x), y =  (x), j (x)≤ y (x) и прямыми x = a, x = b (a ≤ x ≤ b) и пусть по этой криволинейной трапеции равномерно распределена масса, так что поверхностная плотность постоянна. Тогда статические моменты M_x и M_y относительно осей Ox и Oy соответственно, выражаются интегралами

M_x=, M_y=.

Центр тяжести фигуры имеет координаты

x_c=, y_c=,

где S - площадь фигуры.

6.5. Найти координаты центра тяжести фигуры, ограниченной линиями x = 0, x =, y = 0, y = sin x (плотность ρ=1).

Решение. Найдём в начале статические моменты M_x и M_y.

M_x ===.

M_y ====sinx =1.

Найдём площадь фигуры.

S =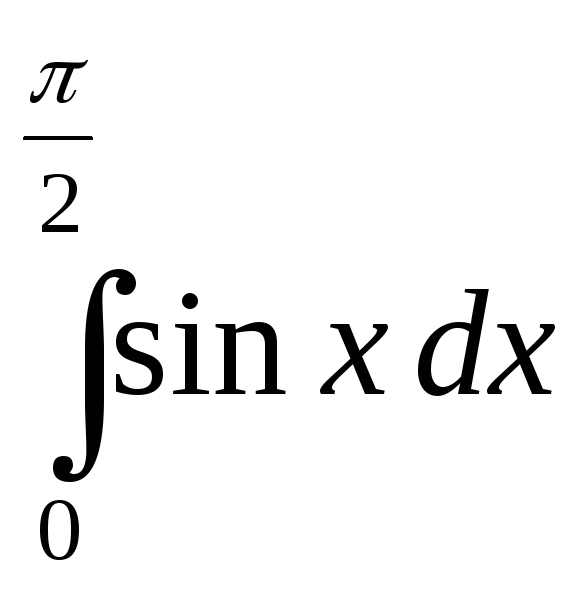==1.

Находим координаты центра тяжести фигуры:

x_c=1, y_c=.

39.

6.6. Скорость точки меняется по закону v =. Найдём путь, пройденный точкой за первые девять секунд после начала движения.

6.7. Реактивный самолёт в течении 20 сек увеличил свою скорость от 360 до 720 . Считая движение самолёта равноускоренным, найти, с каким ускорением летел самолёт и какое расстояние пролетел он за это время.

Указание. Скорость равноускоренного движения выражается формулой v=v₀+at, где v₀ - начальная скорость, a- ускорение, t- время.

6.8. Вычислить силу давления воды (удельный вес γ = 1) на каждую из сторон погружённой вертикально в неё пластинку, имеющую форму равнобедренного треугольника с основанием a м и высотой h м, предполагая, что вершина треугольника лежит на свободной поверхности воды, а основание параллельно ей.

6.9. Какую работу надо совершить, чтобы растянуть пружину на 4 см, если известно, что от нагрузки в 1 н она растягивается на 1см?

6.10. Определить работу, необходимую для запуска ракеты весом P с поверхности Земли вертикально вверх на высоту h.

Указание: F(x)=, где x - расстояние от центра Земли, m_р - масса ракеты, m_з - масса Земли, k - коэффициент пропорциональности, , где R - радиус Земли.

6.11. Вычислить работу, которую нужно затратить на выкачивание воды из котла, имеющего форму полусферы радиуса R.

6.12. Найти координаты центра тяжести фигуры, ограниченной линиями y =2 x - x²,

y =0 (плотность ρ=1).