Основные задачи расчетных заданий I семестра обучения по курсу «Сопротивление материалов» задание № 1

Номер

задания

Название

задания

Цели задания

Название

раздела

задания

Число

типов

расчетных

схем

Охватываемые

темы курса

Сопряженные

темы курса

Сопутствующие учебные дисциплины

1

2

3

4

5

6

7

8

1

Центральное растяжение-сжатие прямого бруса

1) Освоение методики анализа компонент напряженно-деформированного состояния прямого бруса при растяжении-сжатии

2) Освоение методики решения статически неопределимых задач при растяжении-сжатии прямого бруса

3) Освоение методики расчетов на прочность и жесткость при растяжении-сжатии

4) Обучение иерархи-ческим алгоритмам расчетов на прочность при комбинированном нагружении при растяжении-сжатии

ЗАДАЧА № 1:

Расчет статически неопределимого прямого ступенчатого бруса при сило-вом нагружении продольными нагрузками

1

1) Анализ напряженного состояния при силовом нагружении

2) Анализ деформированного состояния при силовом нагружении

3) Решение ста-тически неопределимых задач при силовом нагружении

4) Расчет на прочность при силовом нагружении

1) Структурный подход анализа состояния бруса

2) Проектировочный расчет бруса

3) Механические характеристики материалов на растяжение-сжатие

1) Арифметика

2) Алгебра

3) Физика

4) Высшая математика

5) Черчение

6) Теоретическая механика

7) Технология конструкционных материалов

1

2

3

4

5

6

7

8

ЗАДАЧА № 2:

Расчет статически неопределимого прямого ступен-чатого бруса при тепловом нагружении

1

1) Анализ напряженного состояния при тепловом нагружении

2) Анализ деформированного состояния при тепловом нагружении

3) Решение статически неопределимых задач при тепловом нагружении

ЗАДАЧА № 3:

Расчет запаса прочности прямого бруса при комбиниро-ванном нагруже-нии

1

Методы расчета конструкций

1) Использование принципа суперпозиции при решении задач курса

2) Поверочный расчет бруса

1) Арифметика

2) Алгебра

3) Черчение

1

Центральное растяжение-сжатие системы прямых брусьев

1) Освоение простейшей методики анализа компонент напряженно-деформированного состояния прямого бруса

2) Освоение методики решения статически неопределимых задач для систем с произвольной геометрией

ЗАДАЧА № 4:

Расчет статически неопределимой шарнирно-стержневой системы при силовом нагружении любых элементов системы

5

1) Анализ напряженного состояния при силовом нагружении

2) Анализ деформированного состояния при силовом нагружении

3) Решение стати-чески неопреде-лимых задач при

1) Структурный подход анализа состояния бруса

2) Проектировочный расчет бруса

3) Механические

1) Арифметика

2) Алгебра

3) Геометрия

4) Тригонометрия

5) Физика

5) Высшая математика

6) Черчение

1

2

3

4

5

6

7

8

3) Освоение методики расчетов на прочность и жесткость

4) Обучение иерархи-ческим алгоритмам расчетов на прочность при комбинированном нагружении

силовом нагруже-нии

4) Расчет на прочность при силовом нагружении

характеристики материалов на растяжение-сжатие

7) Теоретическая механика

8) Технология конструкционных материалов

ЗАДАЧА № 5:

Расчет статически неопределимой шарнирно-стержневой системы при тепловом нагружении деформируемых элементов системы

5

1) Анализ напряженного состояния при тепловом нагружении

2) Анализ деформированного состояния при тепловом нагружении

3) Решение статически неопределимых задач при тепловом нагружении

ЗАДАЧА № 6:

Расчет запаса прочности шарнирно-стержневой системы при комбинирован-ном нагружении

5

Методы расчета конструкций

1) Использование принципа суперпозиции при решении задач курса

2) Поверочный расчет бруса

1) Арифметика

2) Алгебра

3) Черчение

Пункт

алгоритма

Название

Расчетная формула,

Действие

Простейшая иллюстрация

1

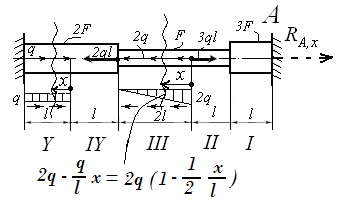
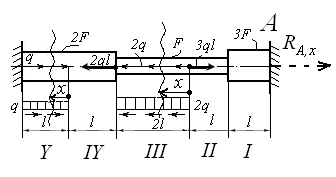
Применение метода

сечений к опоре бруса.

Выделение расчетных

участков бруса.

Применить аксиому о связях теоретической механики. Связь не отбрасывать. Поэтому реакцию R_A,x не отброшенной связи изображать только пунктиром!

2

Расчет перемещения правой опоры по принципу независимости действия сил :

Условие совместности перемещений

участков бруса

3

Расчет компонент перемеще-ния дополнительной опоры бруса ОТ ВСЕХ ВНЕШНИХ НАГРУЗОК

Типы формул расчета ( ПОМНИТЬ И ЗНАТЬ ) :

4

Расчет реакции дополни-тельной связи

5

Расчет функций внутренних сил

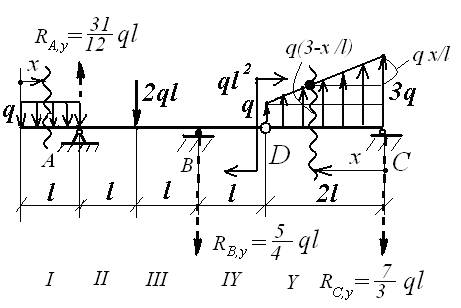
Метод сечений  для внутренних силовых факторов бруса (ВСФ) :

для расчета ЛЮБОГО из ВСФ в ЛЮБОМ сечении ЛЮБОГО бруса ДОСТАТОЧНО алгебраически

(  ) сложить ВСЕ ВНЕШНИЕ силы (моменты сил), включая найденные реакции опор, ТОЛЬКО ПО ОДНУ ЛЮБУЮ сторону от избранного или заданного сечения стрежня

;

6

Расчет изменений длин участков

Типы формул даны в пункте 3 алгоритма:

7

Проверка решения задачи

8

Построение эпюр

1) Построение эпюры см. ДЗ № 1 3)

2) 4)

9

Использование эпюр

Эпюры использовать по конкретике варианта задачи

Вид дифференциального

уравнения

по структурной формуле

Расчетная формула МНП

Вид нагрузки

Простейшая иллюстрация

Кручение : абсолютно те же действия и лишь

Согласно МНП:

Изгиб сложнее, но алгоритм тот же

Этап 1) функция

q=ax+b

↓

а) найти значение q(x) с использованием

значений распределенной нагрузки на концах участка Y ( 3q при x=0 и

q при x=2l , данных по расчетной схеме)

б) в итоге получаем полную квадратичную параболу

Этап 2) функция

а)

б) в итоге получаем кубическую параболу

Знак «-« учитывает направление интегрирования справа налево на участке Y.

Б) Можно обойтись для линейно изменяющейся нагрузки и без интеграла а), если нагрузку в виде трапеции с переменным основанием х разбить на прямоугольник и треугольник с тем же основанием х. Их высоты соответственно и . Точки приложения равнодействующих (выделены на рисунке жирными точками) соответственно х/2 и х/3 от точки С, т.е. их плечи равны

х/2 и 2х/3, а далее применить теорему Пуансо из теоретической механики.

ЗАМЕЧАНИЕ: 1) В отличие от «традиционных» курсов математического анализа в прикладных дисциплинах используется исключительно метод начальных параметров (МНП) при построении функций решения дифференциальных уравнений. Формальные, не имеющие никакого смысла «произвольные константы» никому не нужны! Осмысленная замена этих констант, безусловно, изменяет форму функций решения дифференциального уравнения (это минус), но зато придает «константам» четкий смысл значений искомых функций в начале участка интегрирования дифференциальных уравнений. Заодно это открывает путь многим мощным методам решения, таким, например, как методы прогонки и ортогонализации интегрирования плохо обусловленных уравнений, где формальная математика и даже «высшая» пасует полностью. Формально при этом «всего лишь» абстрактный неопределенный интеграл заменяется на интеграл с переменным пределом. Но для курса сопротивления материалов невозможно придумать более мощной процедуры преобразования, так сразу же становится возможным использование геометрического смысла определенного интеграла. Такой огромный выигрыш окупает любые минусы МНП.

2) «Трапеция» еще раз подчеркивает бессмысленность формального отношения к математике, но уже на уровне геометрии. Согласно «традиционной» геометрии у трапеции есть два основания и одна высота. Но «трапеции» с наклонными боковыми сторонами опять же никому не нужны в прикладных дисциплинах и даже в математическом анализе, о чем «стыдливо» умалчивают во всех средних школах. В математическом анализе, во всех прикладных дисциплинах, связанных с исследованием функций одного или нескольких аргументов у «трапеций» всего одно основание: изменение аргумента функции и две высоты. Поэтому при формальном привлечении геометрии легко ошибаться в расчете площадей эпюр с трапециедальным видом. Везде, кроме бюрократической геометрии: площадь трапеции равна произведению единственного основания на полусумму двух ее высот ( у «бюрократов» - все наоборот)! К высшей школе, высшей математике, функциональному и математическому анализам, не говоря уж о прикладных дисциплинах, средние школы на допустимом рациональном уровне никого не готовят! Учитесь тогда и математике и теоретической механике, как и механике и логике как таковым у сопротивления материалов!

Пункт

алгоритма

Название

Расчетная формула,

Действие

Простейшая иллюстрация

1

Применение метода

сечений к опоре бруса

Применить аксиому о связях теоретической механики. Связь не отбрасывать. Поэтому реакцию не отброшенной связи изображать только пунктиром!

2

Расчет перемещения правой опоры :

Условие совместности перемещений

участков бруса

3

Расчет компонент перемеще-ния дополнительной опоры бруса

Типы формул :

4

Расчет реакции дополни-тельной связи

6

Расчет изменений длин участков

Типы формул даны в пункте 3 алгоритма

7

Проверка решения задачи

8

Построение эпюр

1) Построение эпюры см. ДЗ № 1 3)

2) 4)

9

Использование эпюр

Эпюры использовать по конкретике варианта задачи